A short linear object is placed at a distance u along the axis of a spherical mirror of focal length f.
a. Obtain an expression for the longitudinal magnification.
b. Also, obtain an expression for th eration of the velocity of image (v) to the velocity of the object (u).
a. Mirror formula :1v+1u=1f
On differenciating both sides, we get
−dvv2−duu2=0ordv=−du(vu)2
Since vu=fu−f, therefore
dv=−du(fu−f)2
Lateral magnification, m2=dvdu=−(fu−f)2
The negative sign shows that the image is longitudinally inverted.
b. Since velocity of object, U=dudt
and velocity of image,
V=dvdt
∴V=−U(fu−f)2 or VU=−(fu−f)2
The negative sign shows that the object and image always move in opposite directions.
v=−xf0f0−x
v becomes negative (real image) only when x<f0.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.325videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.412videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.114videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK1videos
FRICTION
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank39videos
GRAVITATION
Similar Questions
A point object is placed at a distance 30 cm in front of a concave mirror of focal length 20 cm. Find the nature and location of image obtained.
View SolutionAn illuminated object is placed at a distance of 20 cm from a converging lens of focal length 15 cm. The image obtained on the screen is:
View Solution
Knowledge Check
- Question 1 - Select One
A short linear object of length b lies on the axis of a concave mirror of focal length F at a distance u from the pole. The length of the image will be
A(fu−f)bB(u−ff)bC(fu−f)2bD(u−ff)2b - Question 2 - Select One
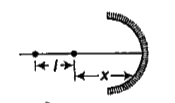
A short linear object of length l lies on the axis of a spherical mirror of focal length f, at a distance x from the mirror. Then, the length of the image (P) so obtained will be
 AIf(x−f)BIf2(x−f)2CIfxDI(x−f)x
AIf(x−f)BIf2(x−f)2CIfxDI(x−f)x - Question 3 - Select One
A point object is placed on the principal axis of a spherical mirror. The object -distance u is
Adefinitely negativeBdefinitely positiveCpositive if the object is to the left of the centre of curvatureDpositive if the object is to the right of the centre of curvature
Calculate the distance of an object of height h from a concave mirror of focal length 10cm so as to obtain a real image of magnification 2.
View SolutionA short linear object of length l lies on the asix of a spherical mirror of focal length f, at a distance x from the mirror. Then, the length of the image (P) so obtained will be
 View Solution
View SolutionA short linear object of length / lies along the axis of a concave mirror of focal length f at a distance d from the pole of the mirror. The approximate size of the image is
View SolutionA linear object is placed along the axis of a mirror as shown in figure. If 'f' is the focal length of the mirror then the length of image is-
 View Solution
View SolutionA short linear object of length b lies along the axis of a concave mirror of focal length f at a distanee u from the pole of the mirror. The size of the image is approximately equal to
View Solution

