A linear object is placed along the axis of a mirror as shown in figure. If 'f' is the focal length of the mirror then the length of image is-

2f3
f
f3
None of these
The correct Answer is:B
LiL0=−(−f)2(−32f+f)(−2f+f)
=−f2(−f2)(−f)=2
Li=2L0=2(2f−32f)=f
Topper's Solved these Questions
Similar Questions
An object of length 2.5 cm is placed at a distance of 1.5 f from a concave mirror where f is the focal length of the mirror. The length of object is perpendicular to principal axis. Find the size of image. Is the image erect or inverted?
View SolutionA short linear object of length l lies on the axis of a spherical mirror of focal length f, at a distance x from the mirror. Then, the length of the image (P) so obtained will be

View Solution
Knowledge Check
A point object is placed on the axis of the concave mirror at a distance of 60 cm from the focal point of the mirror. Its image is formed at the point of object then focal length of the mirror is
A15 cmB30 cmC60 cmD120 cmA linear object AB is placed along the axis of a concave mirror. This object is moving towards the mirror with speed U. The speed of the image of the point A is 4U and the speed of the image of B is alSO 4U btu in opposite direction. If the center of the line AB is at a distance L from the mirror then find out the length of the object.
 A3L/2B5L/3CLDNone of these
A3L/2B5L/3CLDNone of theseAn object is placed on the principal axis of a concave mirror at a distance of 1.5 f(f is the focal length). The image will be at,
A1.5fB−1.5fC3fD−3f
A short linear object of length b lies on the axis of a concave mirror of focal length F at a distance u from the pole. The length of the image will be
View SolutionAn object is placed in front of a convex mirror at a distance equal to the focal length of the mirror. If its focal length is 20 cm, the distance of the image from the mirror is ______ cm
View SolutionThe distance of an object from a spherical mirror is equal to the focal length of the mirror. Then the image.
View SolutionThe distance of an object from a spherical mirror is equal to the focal length of the mirror. Then the image:
View SolutionA short linear object of length l lies on the asix of a spherical mirror of focal length f, at a distance x from the mirror. Then, the length of the image (P) so obtained will be
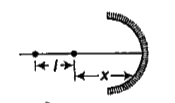
View Solution
