A convex mirror and a concave mirror of radius 10cm each are placed 15cm apart facing each other. An object is placed midway between them. If the reflection first takes place in the concave mirror and then in convex mirror, the position of the final image is
on the pole of the convex mirror
on the pole of the concave mirror
at a distance of 10cm from the convex mirror
at a distance of 5cm from the concave mirror
The correct Answer is:a.
To solve the problem step by step, we will follow the sequence of reflections as described in the question.
Step 1: Understand the Setup
We have a concave mirror and a convex mirror, both with a radius of curvature R=10cm. The focal lengths (f) of the mirrors can be calculated as:
- For the concave mirror: f=−R2=−102=−5cm
- For the convex mirror: f=R2=102=5cm
The distance between the two mirrors is 15cm, and the object is placed midway, which means it is 7.5cm from each mirror.
Step 2: Reflection in the Concave Mirror
The object distance (u) for the concave mirror is:
u=−7.5cm(negative because it is in front of the mirror)
Using the mirror formula:
1f=1v+1u
Substituting the values:
1−5=1v+1−7.5
Rearranging gives:
1v=1−5+17.5
Finding a common denominator (which is 15):
1v=−315+215=−115
Thus,
v=−15cm
This indicates that the image formed by the concave mirror is virtual and located 15cm behind the mirror.
Step 3: Use the Image from the Concave Mirror as the Object for the Convex Mirror
The distance of this virtual image from the convex mirror is:
u′=15cm+7.5cm=22.5cm(positive because it is in front of the convex mirror)
Now, we will use this object distance for the convex mirror:
u′=−22.5cm
Using the mirror formula for the convex mirror:
1f=1v′+1u′
Substituting the values:
15=1v′+1−22.5
Rearranging gives:
1v′=15+122.5
Finding a common denominator (which is 22.5):
1v′=4.522.5+122.5=5.522.5
Thus,
v′=22.55.5≈4.09cm
Final Position of the Image
The final image formed by the convex mirror is approximately 4.09cm in front of the convex mirror.
Summary of Steps
1. Calculate the focal lengths of both mirrors.
2. Determine the object distance for the concave mirror.
3. Use the mirror formula to find the image distance from the concave mirror.
4. Calculate the new object distance for the convex mirror using the image from the concave mirror.
5. Use the mirror formula again to find the final image distance from the convex mirror.
We have a concave mirror and a convex mirror, both with a radius of curvature R=10cm. The focal lengths (f) of the mirrors can be calculated as:
- For the concave mirror: f=−R2=−102=−5cm
- For the convex mirror: f=R2=102=5cm
The object distance (u) for the concave mirror is:
u=−7.5cm(negative because it is in front of the mirror)
1f=1v+1u
Substituting the values:
1−5=1v+1−7.5
Rearranging gives:
1v=1−5+17.5
Finding a common denominator (which is 15):
1v=−315+215=−115
Thus,
v=−15cm
This indicates that the image formed by the concave mirror is virtual and located 15cm behind the mirror.
The distance of this virtual image from the convex mirror is:
u′=15cm+7.5cm=22.5cm(positive because it is in front of the convex mirror)
u′=−22.5cm
1f=1v′+1u′
Substituting the values:
15=1v′+1−22.5
Rearranging gives:
1v′=15+122.5
Finding a common denominator (which is 22.5):
1v′=4.522.5+122.5=5.522.5
Thus,
v′=22.55.5≈4.09cm
The final image formed by the convex mirror is approximately 4.09cm in front of the convex mirror.
1. Calculate the focal lengths of both mirrors.
2. Determine the object distance for the concave mirror.
3. Use the mirror formula to find the image distance from the concave mirror.
4. Calculate the new object distance for the convex mirror using the image from the concave mirror.
5. Use the mirror formula again to find the final image distance from the convex mirror.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Assertion-Reasoninig
Explore 2 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Linked Comprehension
Explore 51 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Subjective
Explore 26 Videos
- FRICTIONBook:CENGAGE PHYSICSChapter:FRICTIONExercise:QUESTION BANK
Explore 1 Video
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:Question Bank
Explore 39 Videos
Similar Questions
A convax and a concave mirror each of radius 10cm are placed facing eachother at 15cm distance. A point object is placed midway between them. Find the position of the final image if reflection takes place first at the concave mirror and then convex mirror.
View Solutiona concave mirror of focal length 20cm and a convex mirror of focal length 15cm are placed 50cm apart, such that the two mirrors face eaachother. An object is placed exactly midway between them. Fing the nature and position of image formed by reflection first at concave mirror and then at convex mirror.
View Solution
Knowledge Check
A convex and a concave mirror of radii 10 cm are placed facing each other and 15 cm apart. An object is placed exactly between them. If the reflection first takes place in concave and then in convex mirror the position of the final image will be
A7 cm behind concave mirrorBat the pole of the concave mirrorCat the pole of the convex mirrorD6.7 cm in front of concave mirrorA concave mirror of focal length 10cm and a convex mirror of focal length 15cm are placed facing each other 40cm apart. A point object is placed between the mirrors, on their common axis and 15cm from the concave mirror. Find the position and nature of the image produced by successive reflections, first at the concave mirror and then at the convex mirror.
A12cm behind convex mirror, realB9cm behind convex mirror, realC6cm behind convex mirror, virtualD3cm behind convex mirror, virtualTwo mirrors, one concave and the other convex, are placed 60 cm apart with their reflecting surfaces facing each other. An object is placed 30 cm from the pole of either of them on their axis. If the focal lengths of both the mirrors are 15 cm, the position of the image formed by reflection, first at the convex and then at the concave mirror, is:
A19.09 cm from the pole of the concave mirrorB19.09 cm from the pole of the convex mirrorC11.09 cm from the pole of the concave mirrorD11.09 cm from the pole of the convex mirror
A concave mirror and a plane mirror are arranged facing each other and an object AB is placed between them as shown in the figure. What is the distance between the object and its inverted, virtual image formed in plane mirror?
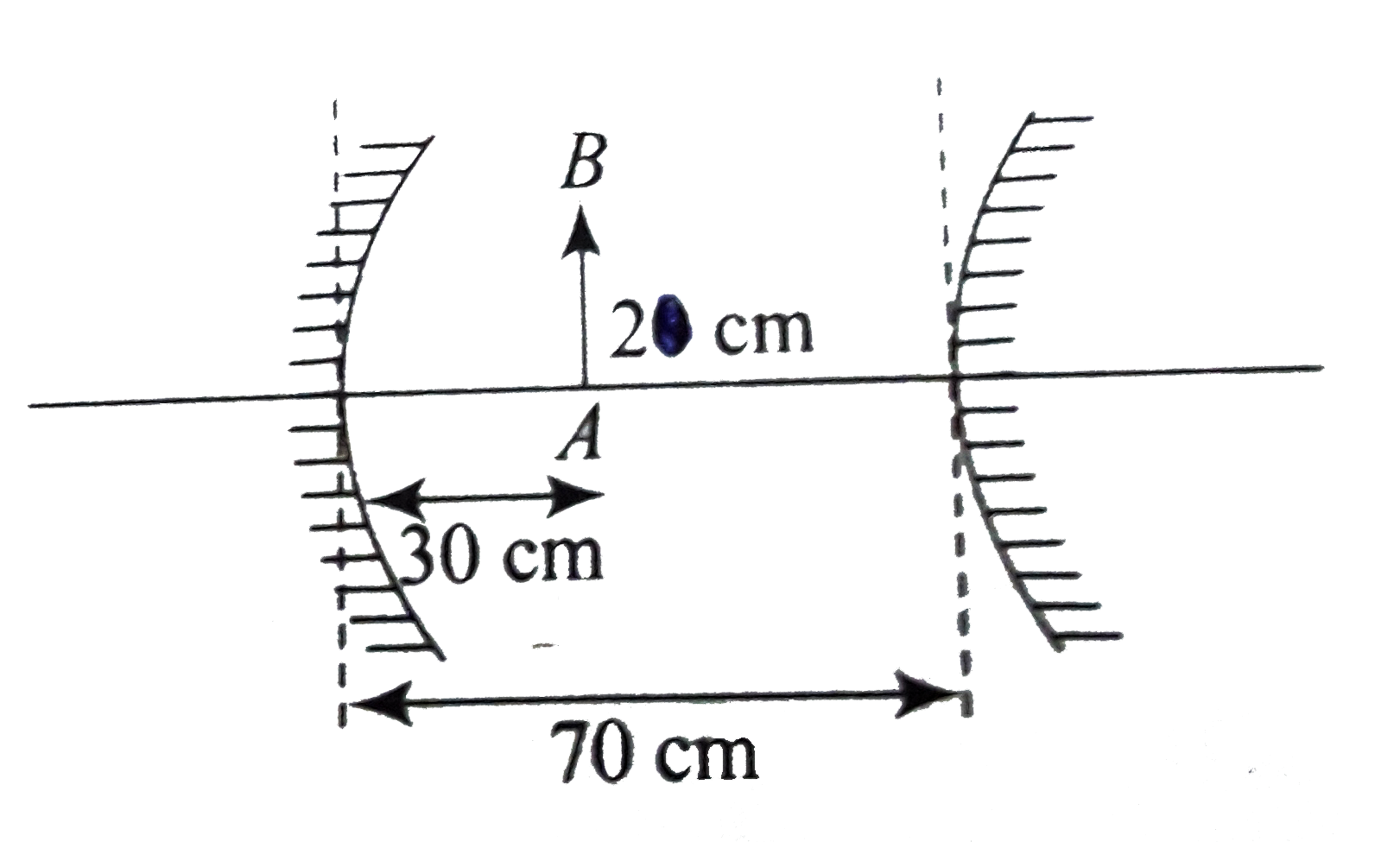
View SolutionA concave mirror and a convex mirror of focal lengths 10cm and 15cm are places at a distance of 70cm. An object AB of height 2cm is places at a distance of 30cm from the concave mirror. First ray is incident on the concave mirror then on the convex mirror. Find size, position, and nature of the image.
View SolutionAn object is placed between a plane mirror and a concave mirror of focal length 15 cm as shown in Figure . Find the position of the images after two reflections.

View SolutionTwo plane mirrors parallel to each other and an object O placed between them. Then the distance of the first three images from the mirror M2 will be (in cm) –

View SolutionTwo mirrors, one concave and the other convex, are placed 60 cm apart with their reflecting surfaces facing each other . An object is placed 30 cm from the pole of either of them on their axis. If the focal lengths of both the mirrors are 15 cm , the position of the image formed by reflection, first at the convex and then at the concave mirrors , is
View Solution
