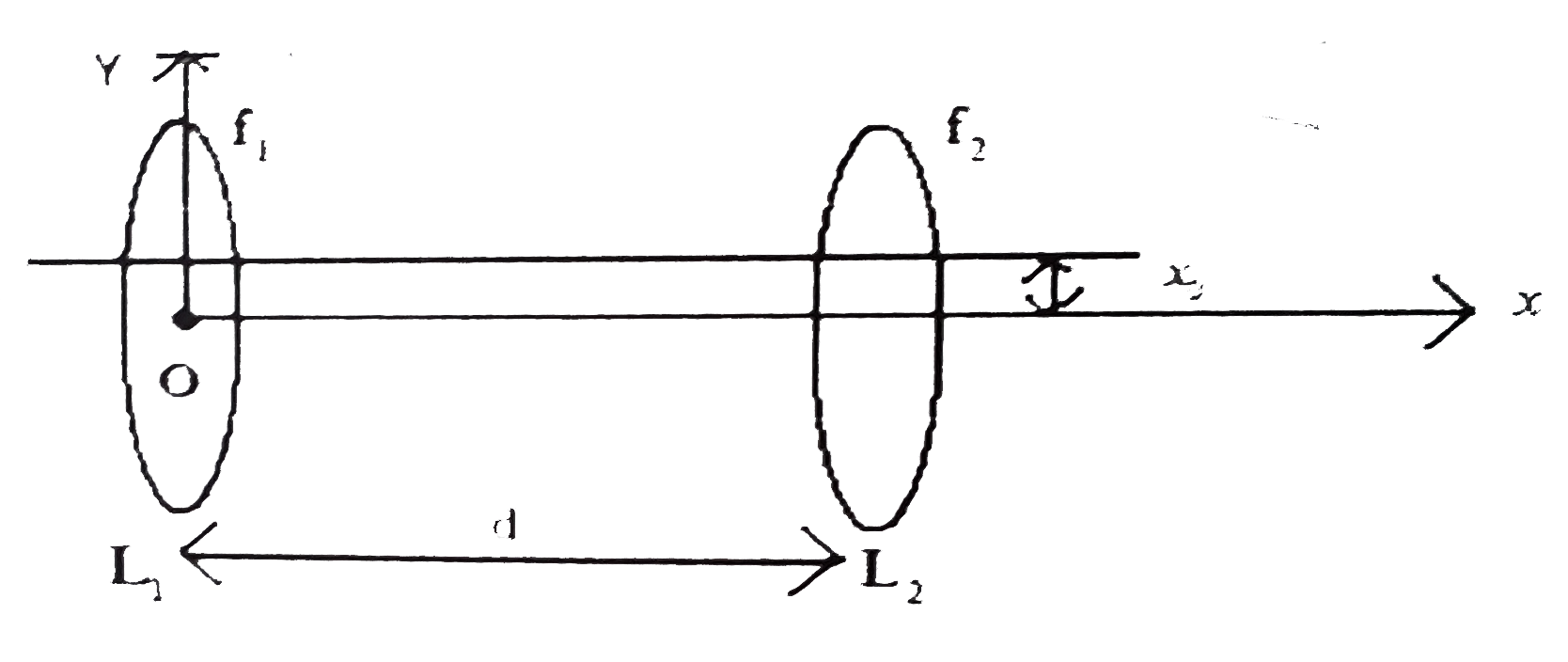
Two thin convex lenses of focal lengths f1 and f2 are separated by a horizontal distance d (whered<f1,d<f2) and their centres are displaced by a vertical separation △ as shown in the fig.
Taking the origin of coordinates O, at the centre of the first lens the x and y coordinates of the focal point of this lens system, for a parallel beam of rays coming form the left, are given by:
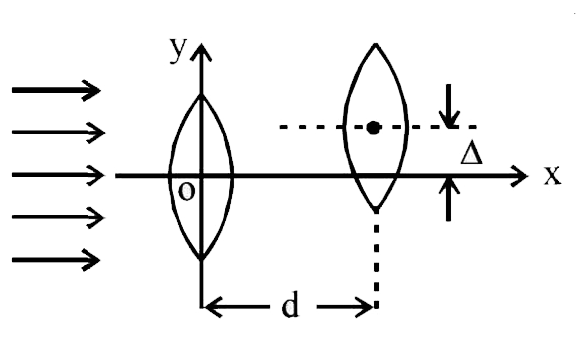
x=f1f2f1+f2,y=Δ
x=f1(f2+d)f1+f2−d,y=Δf1+f2
x=f1f2+d(f1−d)f1+f2−d,y=Δ(f1−d)f1+f2−d
x=f1f2+d(f1−d)f1+f2−d,y=Δ(f1−d)f1+f2−d
The correct Answer is:c.
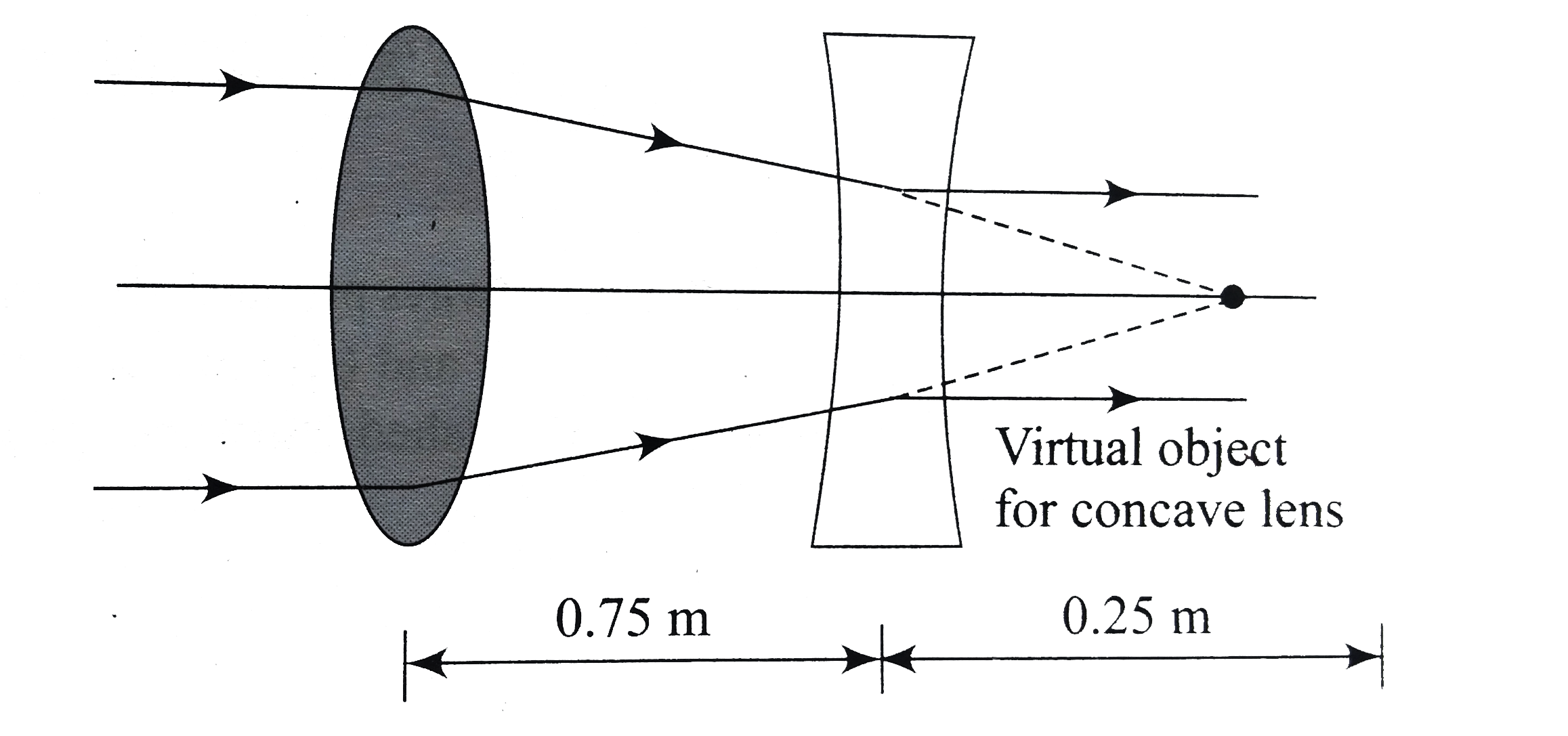
The image I′ of parallel rays formed by lens 1 will act as a virtual object.
Applying lens formula for lens 2,
1v−1u=1f
⇒1v−1f1−d=1f2
⇒v=f2(f1−d)f2+f1−d
The horizontal distance of the image O is
x=d+f2(f1−d)f2+f1−d
=df2+df1−d2+f2f1−df2f2+f1−d
=f1f2+d(f1−d)f2+f1−d
To find teh y-coordinate, we use magnification formula for lens 2,
m=vu=f2(f1−d)f1+f2−df1−d=f2f1+f2−d. Also
m=h2Δ⇒h2=Δ×f2f1+f2−d
Therefore, the y-coordinate,
y=Δ−h2
=Δ−Δf2f1+f2−d
=Δf1+Δf2−Δd−Δf2f1+f2−d=Δ(f1−d)f1−f2−d
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Multiple Correct Answers Type
Explore 8 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Assertion-Reasoninig Type
Explore 2 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:True/False
Explore 5 Videos
- FRICTIONBook:CENGAGE PHYSICSChapter:FRICTIONExercise:QUESTION BANK
Explore 1 Video
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:Question Bank
Explore 39 Videos
Similar Questions
In the figure- it is shown,the focal length f of the two thin convex lenses is the same. They are separated by a horizontal distance 3f and their optical axes are displaced by a vertical separation 'd'(d<<f) as shown. Taking the origin of coordinates O at the centre of the first lens , find the x and y coordinates of the point where aparallel beam of rays coming from the left finally gets focussed ?
((5f, 2d)]
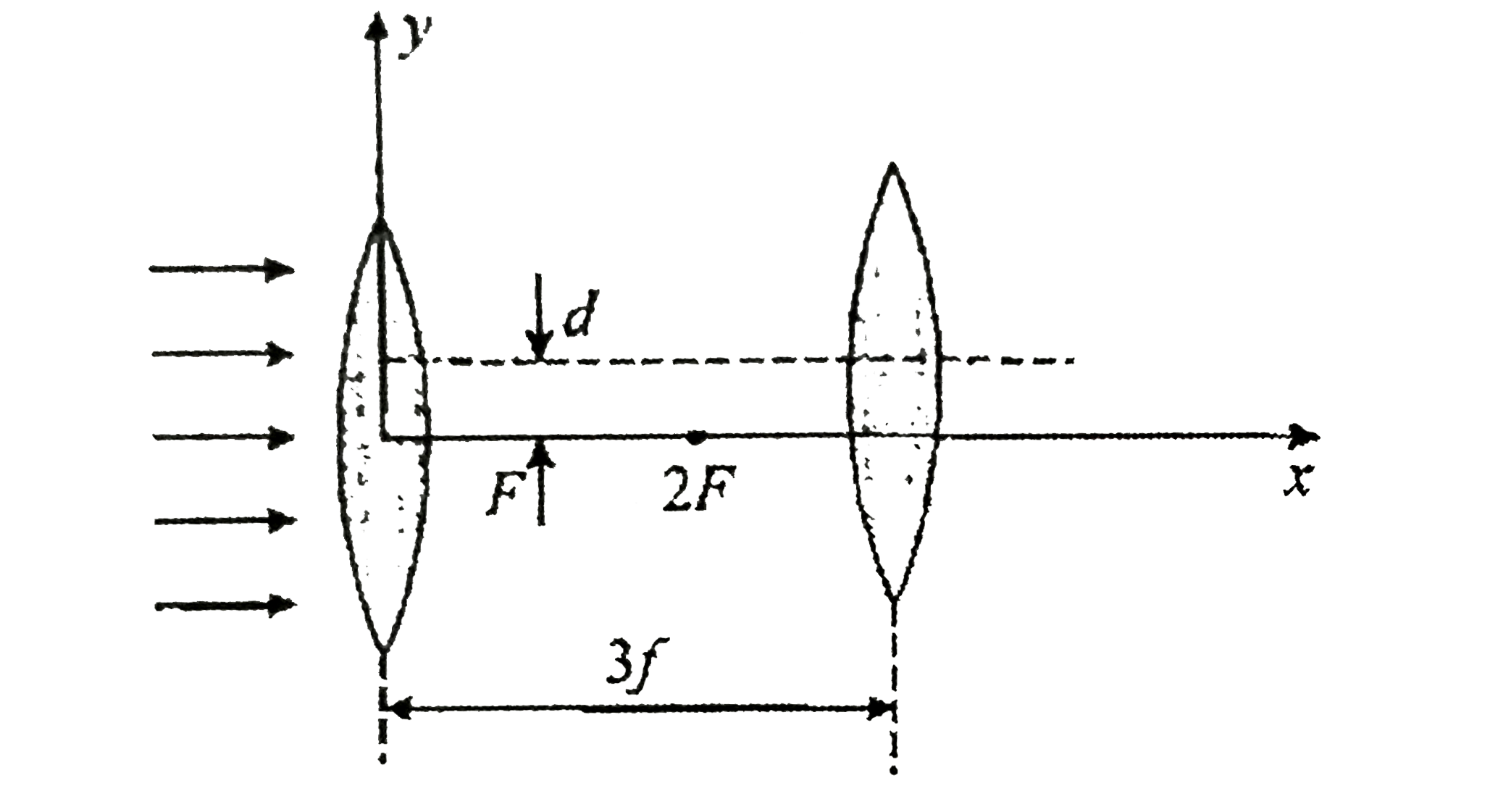
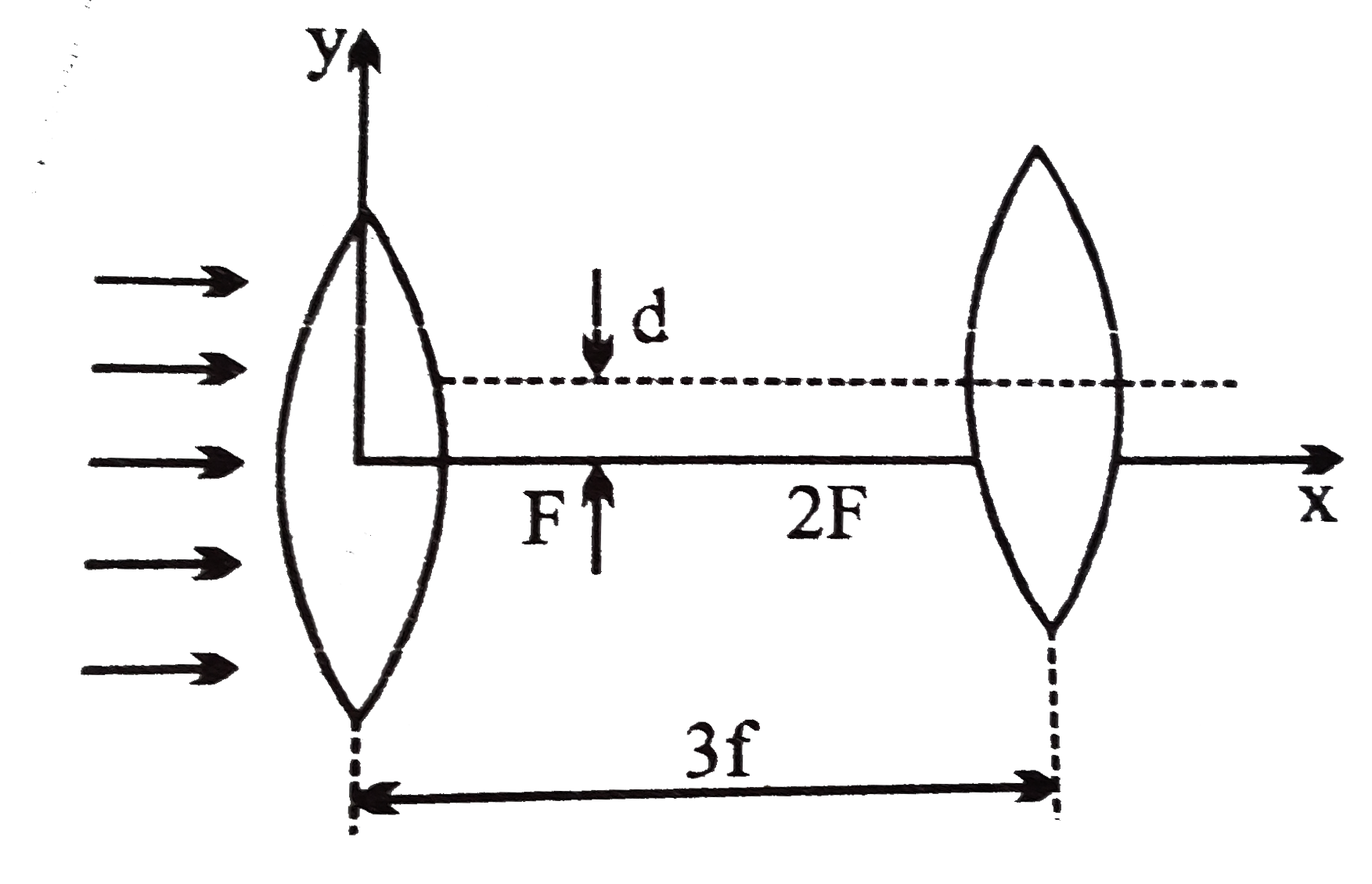
View Solutionthe focal length of the two thin convex lenses is the same=fThey are separated by a horizontal distance3fand their optical axes are displaced by a vertical separation'd'(d<<f) .Taking the origin of coordinatesOat the centre of the first,lens ,find the xand y coordiates of the point where a parallel beamof rays coming from the left finally get focused?
View Solution
Knowledge Check
Two thin convex lenses of focal lengthf1andf2are separated by a horizontal distance'd'where(d<f1andd<f2) and their optical centers are displaced vertically byx0 .Taking the origin at the centre of lens L1consider the following cases when a parallel beam of paraxial rays are coming form left.
x coordinate of the final image isAd(f1+d)+f1f2(f1+f2−d)Bd(f1+d)f1+f2−dCf1+f2D(f1+f2)df1−f2+dTwo thin convex lenses of focal lengthf1andf2are separated by a horizontal distance'd'where(d<f1andd<f2) and their optical centers are displaced vertically byx0 .Taking the origin at the centre of lens L1consider the following cases when a parallel beam of paraxial rays are coming form left.
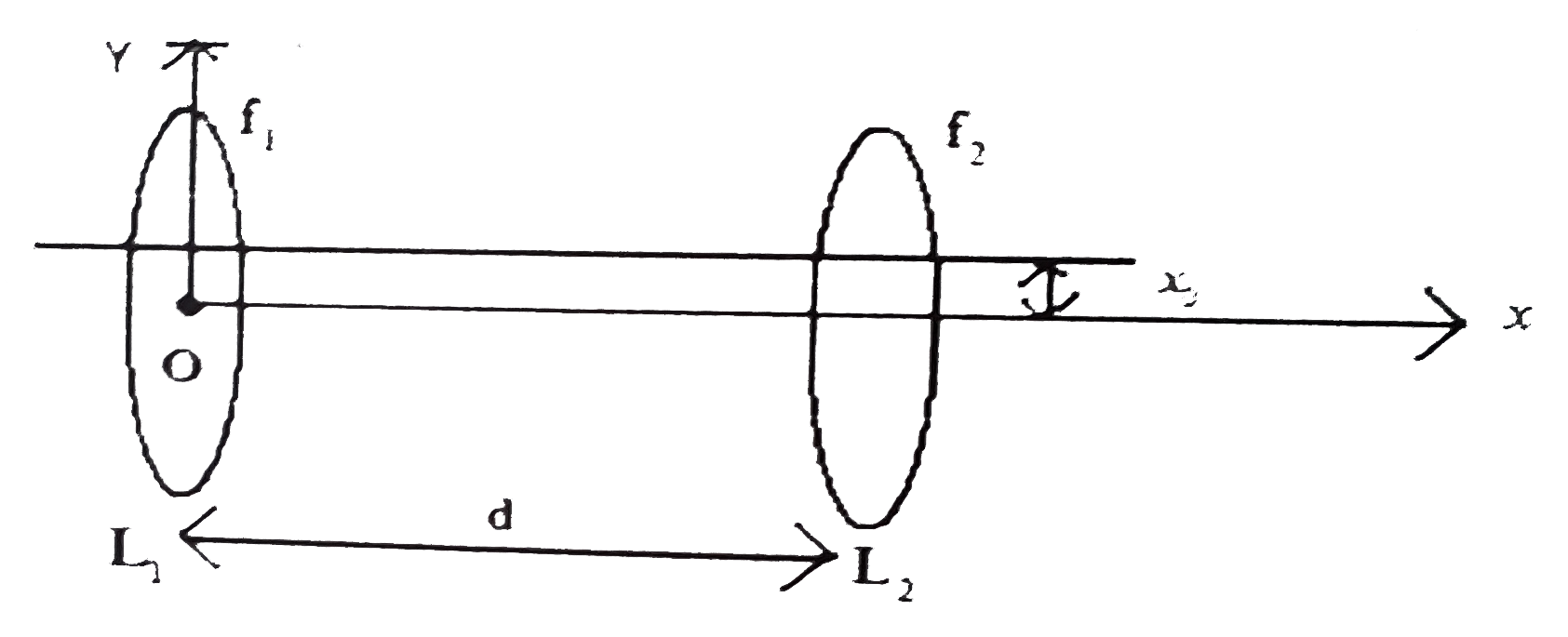
for the lens1 L2,object distance isAf2−f1Bf2+dCf1+dD(f1−d)TTwo thin convex lenses of focal lengthf1andf2are separated by a horizontal distance'd'where(d<f1andd<f2) and their optical centers are displaced vertically byx0 .Taking the origin at the centre of lens L1consider the following cases when a parallel beam of paraxial rays are coming form left.

Y coordinate of the final image is given by:Ax0[f1−d(f1+f2−d)]Bx0Cx0(f1+d)f1+f2Dx0(f1+d)(f1+f2−d)
Two thin convex lenses of focal lengths f1 and f2 are in contact and coaxial. The power of the combination is
View SolutionTwo convex lenses of focal lengths f1andf2 are separated co-axially by a distance d. The power of the combination will be one if
View SolutionTwo thin lenses of focal lengths f1 and f2 are in contact. The focal length of this combination is
View SolutionTwo thin lenses of focal lengths f1andf2 are placed in contact. The focal length of the composite lens will be
View SolutionTwo convex lenses of focal length f1 and f2 are mounted coaxially separated by a distance. If the power of the combination is zero, the distance between the lenses is
View Solution