A diverging beam of light from a point source S having divergence angle α, falls symmetrically on a glass slab as shown. The angles of incidence of the two extrem rays are equal. If the thickness of the glass slab is t and the refractive index n, then the divergence angle of the emergent beam is
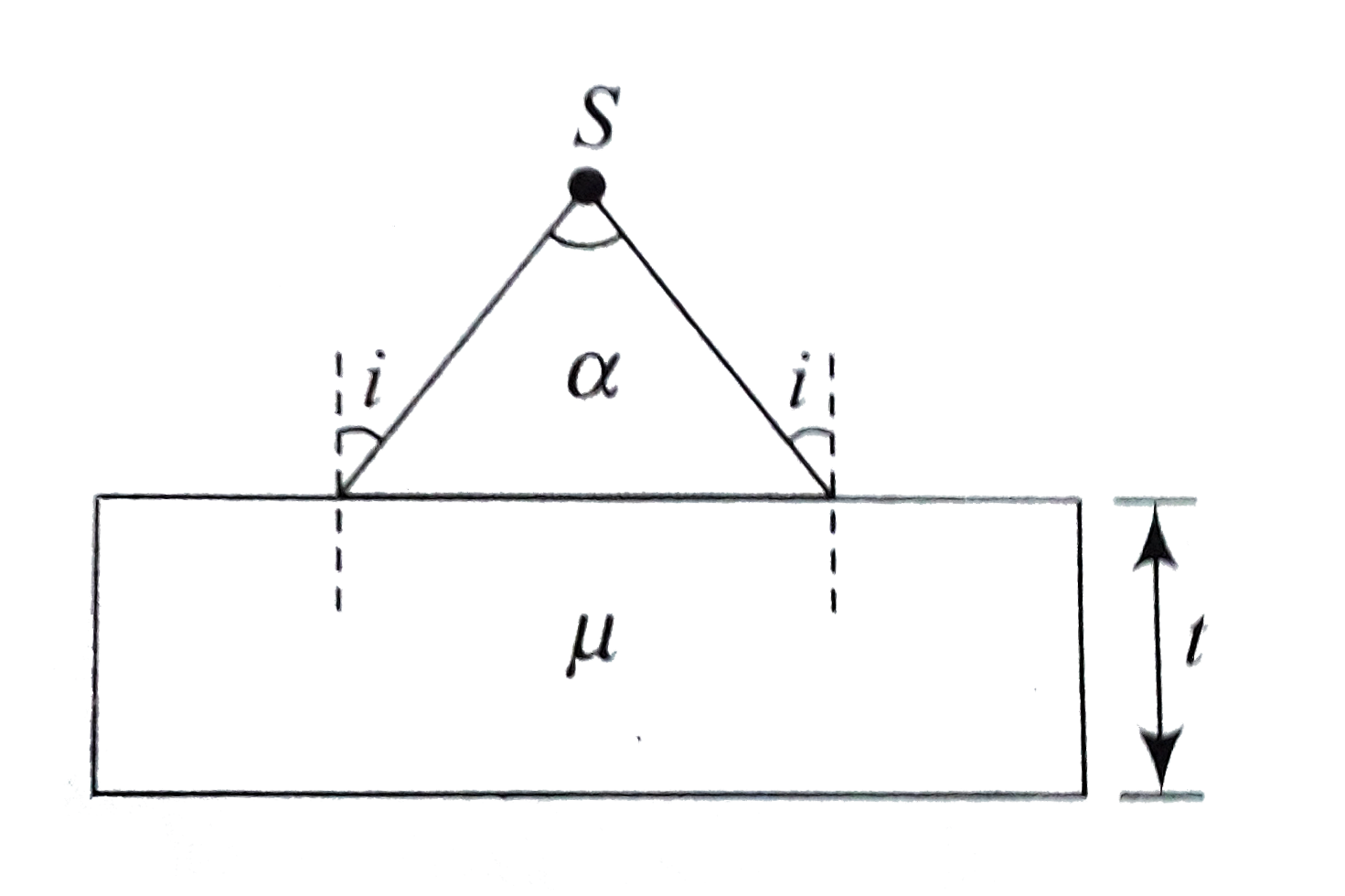
zero
α
sin−1(1n)
2sin−1(1n)
The correct Answer is:b.
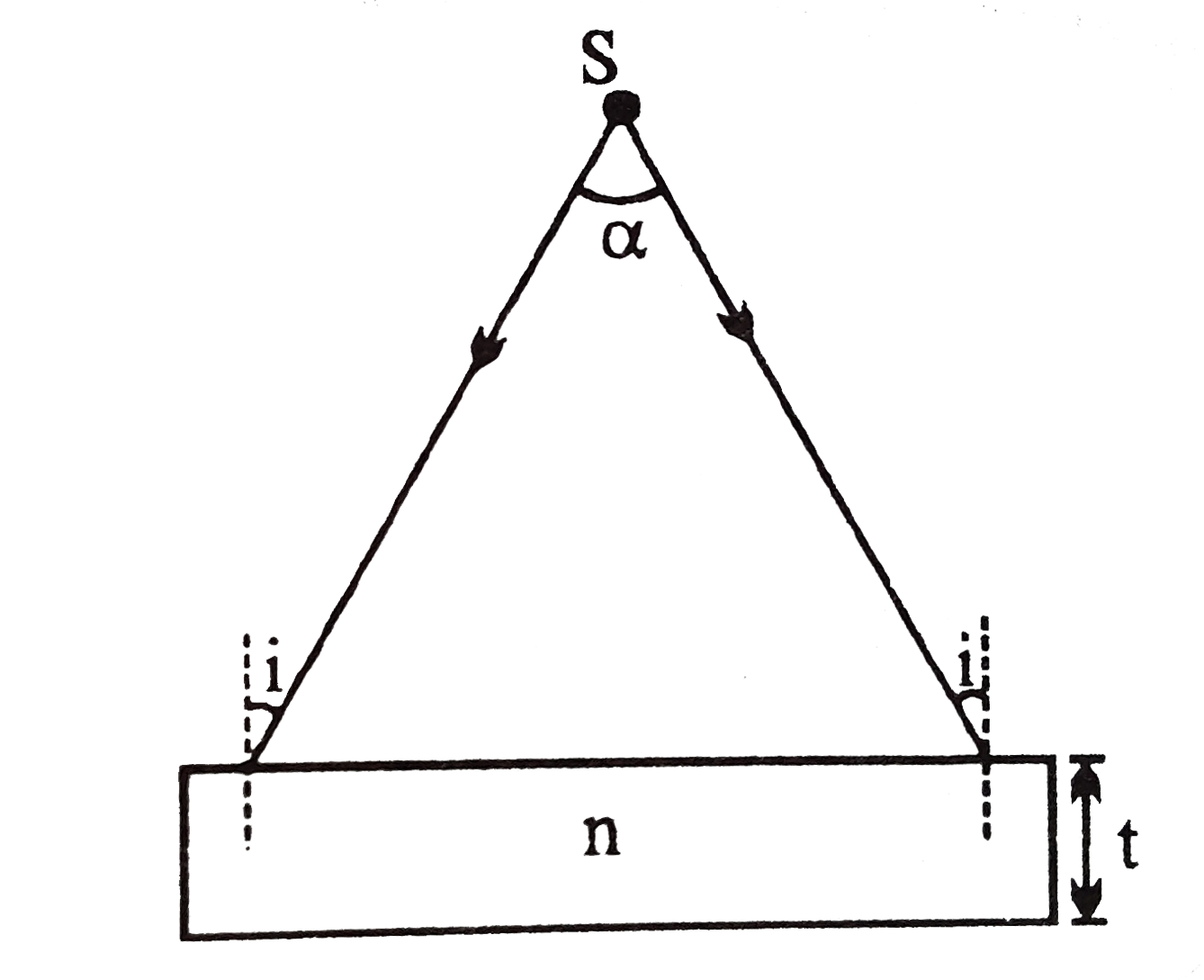
The path of rays become parallel to initial direction as they emerge.
Applying Snell's law at P,12n=sinα/2sinr (i)
Applying Snell's law at Q, 12n=sinβ/2sinr (ii)
From Eqs. (i) and (ii), α=β
Therefore, (b) is the correct answer. ltbgt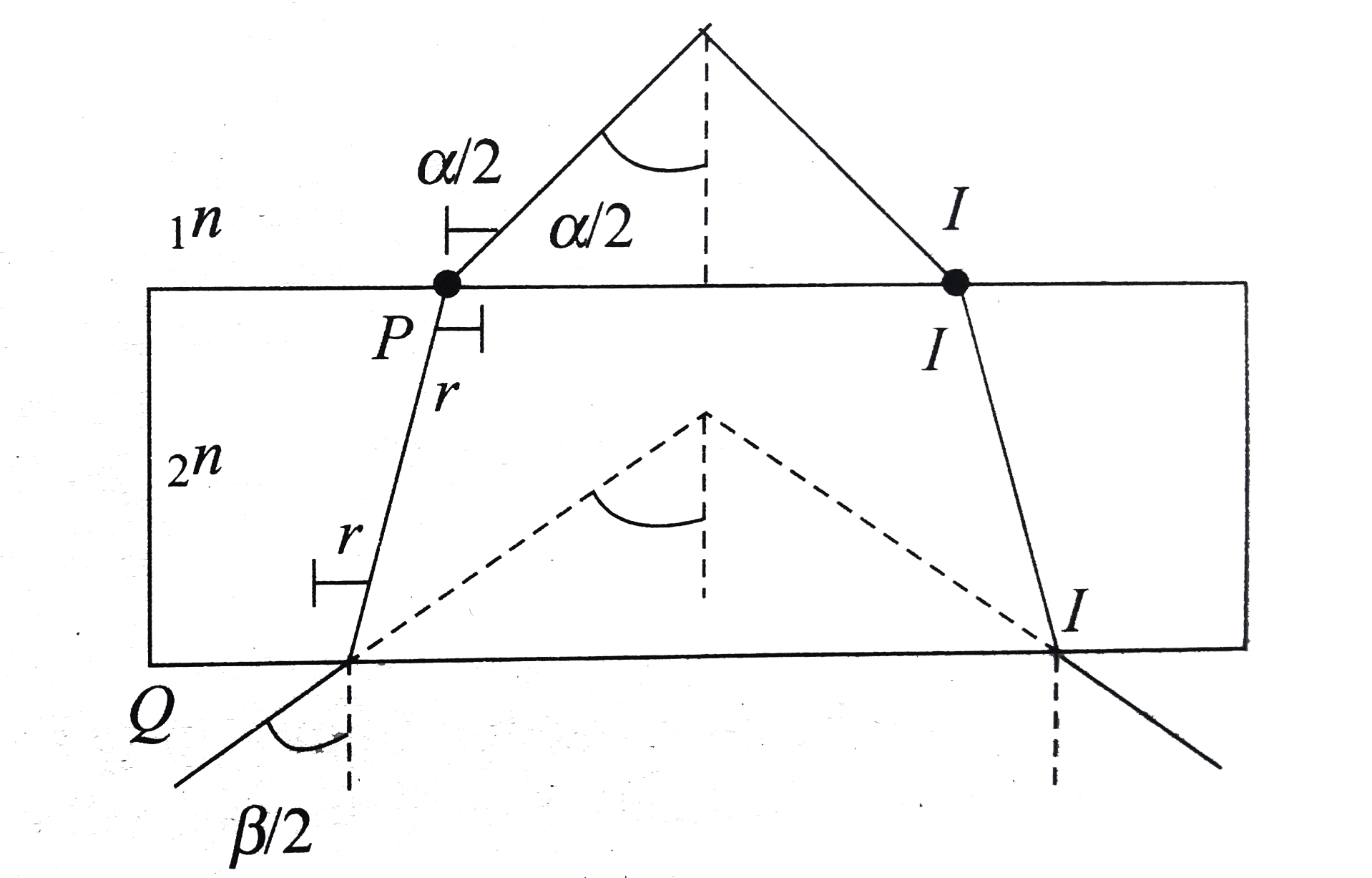 
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Multiple Correct Answers Type
8 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig Type
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - True/False
5 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK
1 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
Similar Questions
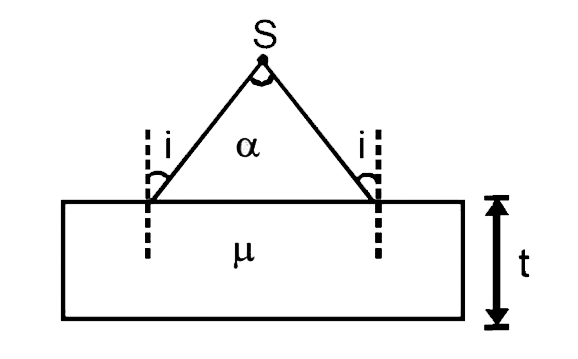
A diverging beam of light from a point source S having devergence angle α, falls symmetrically on a glass slab as shown. The angles of incidence of the two extreme rays are equal. If the thickness of the glass slab is t and the refractive index n, then the divergence angle of the emergent beam is
View SolutionSelect the alternatatives.
(a) A diverging beam of light form a point source S having divergence angle α ,falls symmetrically on a glass slab as shown .the angles of incidence of the two extreme rays are equal .Fi the thickness of the glass slab is tand the refractive index nthe n the divergence angle of the emergent beam is (A) zero,(B) α(C)sin−1(1/n)(D)2sin−1(1/n)
(b) Arectangular glass slab ABCDof refractive index n1 is immersed in water of refractive indexn2(n1>n2) A ray of light is incident at the surface ABof the slab as shown .The maximum value of the angle of incidenc eαmaxsuch that the ray comes out only from the other surface CDis given by
(A) sin−1[n1n2cos(sin−1n2n1)] (B)sin−1[n1n2cos(sin−11n2)](C)sin−1(n1n2)(D)sin−1(n2n1)
(c) A point source of lightB is placed at a distance L inother of the centre of a mirror of width hung vertically ona wall A man walks is front of the mirror along a line parallel to the mirror at a distance 2L from it as shown .the greatest distance over which he can see the image of the light source in the mirror is (A)d/2 (B) d,(c )2d,(d)3d,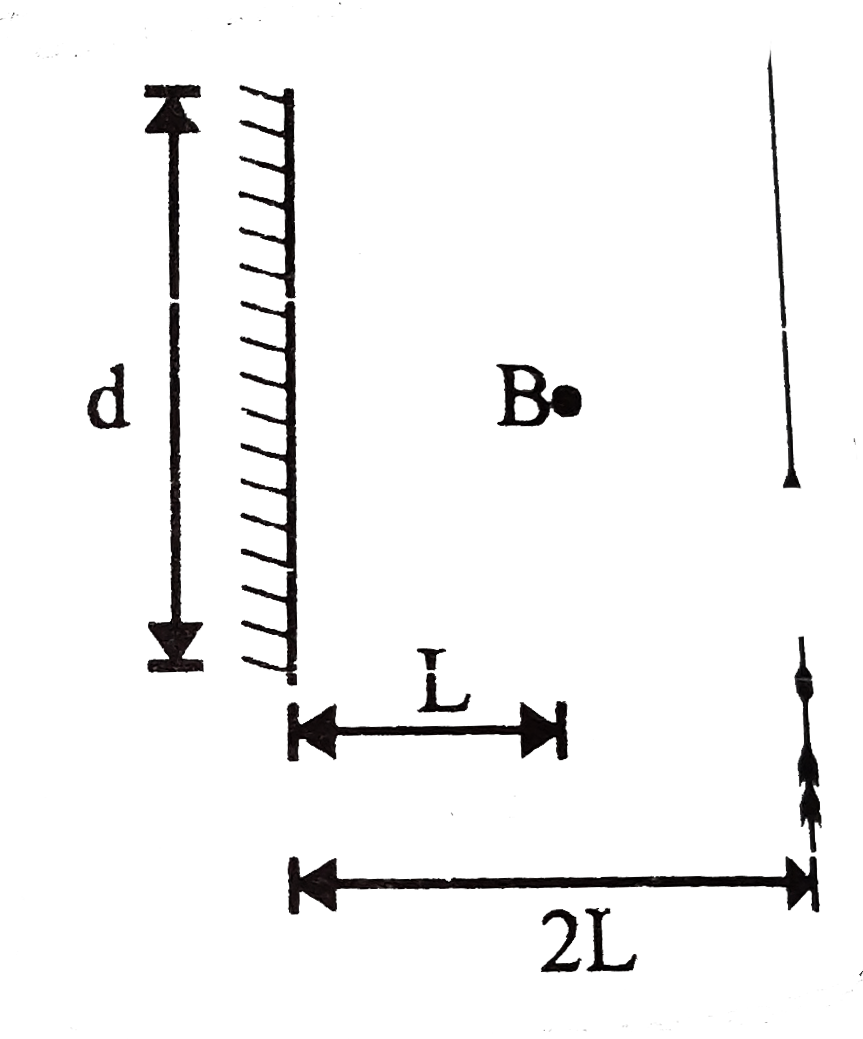
a hollow double concave lens is made of very thin transparents meterial .It can be filled with air or either of two liquids L1andL2having refractive indicesn1andn2respectively(n2>n!>1) the lens will diverge a parallel beam of light of it is filled with (A)air and placed in air.(B) air and immersed inL1(C ),L1 and immersed inL2 (D),L2 ans immersed in L1
View Solution
Knowledge Check
-
A diverging beam of light from a point source S having devergence angle α, falls symmetrically on a glass slab as shown. The angles of incidence of the two extreme rays are equal. If the thickness of the glass slab is t and the refractive index n, then the divergence angle of the emergent beam isAzeroBαCsin−1(1n)D2sin−1(1n) The angle between the incident and the emergent ray from a glass slab is
A90∘B0∘Cless than 90∘Dmore than 90∘A ray of light passes throught a plane glass slab of thickness t and refractive index μ=1.5. The angle between incident ray and emergent ray will be
A0∘B30∘C45∘D60∘
If the angle of incidence and angle of emergence of a light ray falling on a glass slab are I and e respectively, prove that,i=e.
View SolutionIf the angle of incidence and angle of emergence of a light ray falling on a glass slab are i and e respectively, prove that, i = e.
View SolutionAt what angle of incidence should a light beam strike a light beam strike a glass slab of refractive index √3, such that the reflected and refracted rays are perpendicular to each other ?
View SolutionA parallel beam of monochromatic light is incident on a glass slab at an angle of incidence 60∘. Find the ratio of width of the beam in the glass to that in the air if refractive index of glass is 3/2.
View SolutionA paralel beam of monochromatic light is incident on a glass slab at an angle of incidentce 45∘. Find the ratio of width of beam in glass to that in air ( If refractive index of glass is 1.5).
View Solution