In YDSE of equal width slits, if intensity at the center of screen is $I_{0}$ , then intensity at a distance of $β / 4$ from the central maxima is

A

$I_{0}$

B

$\frac{I_{0}}{2}$

C

$\frac{I_{0}}{4}$

D

$\frac{I_{0}}{3}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:b

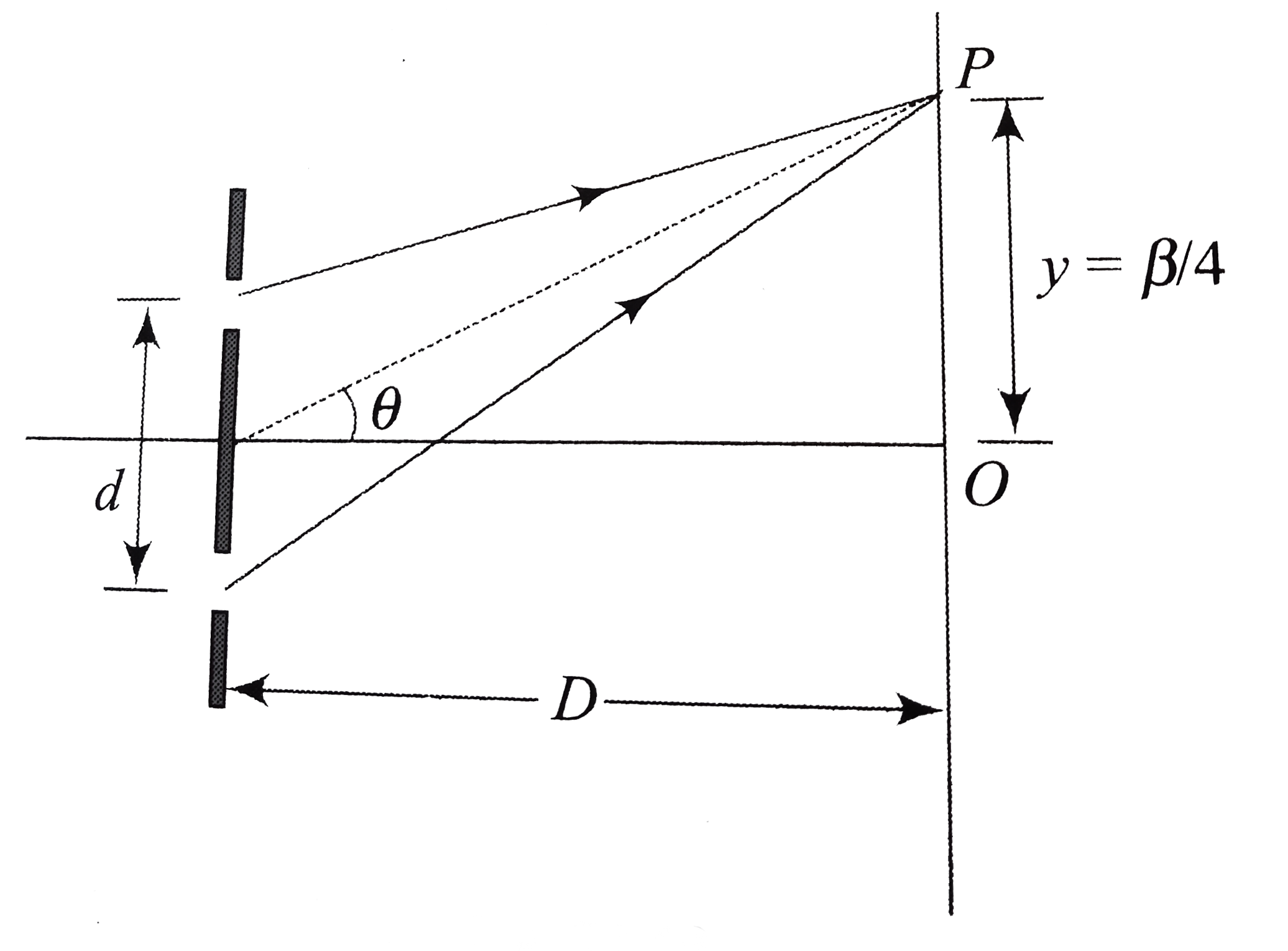
Let the intensity of individual waves be. I Then
$I_{0} = 4 I \Rightarrow I = \frac{I_{0}}{4}$
At P,
$Δ x = d sin θ$
$\Rightarrow Δ x d sin θ = \frac{d y}{D}$
$\Rightarrow Δ x = \frac{d}{D} \times \frac{β}{4} = \frac{d}{D} \times \frac{λ D}{4 d} = \frac{λ}{4}$
$∴ Δ ϕ = \frac{2 π}{λ} \times \frac{π}{4} = \frac{π}{2}$ $[Δ ϕ = k Δ x]$
$I' = I + I + 2 \sqrt{I^{2}} cos (\frac{π}{2}) = 2 I = \frac{I_{0}}{2}$

|

Updated on:21/07/2023

Class 12 PHYSICS WAVE OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In YDSE, having slits of equal width, let $β$ be the fringe width and $I_{0}$ be the maximum intensity. At a distance x from the central brigth fringe, the intensity will be
A $I_{0} cos (\frac{x}{β})$
B $I_{0} {cos}^{2} (\frac{2 π x}{β})$
C $I_{0} {cos}^{2} (\frac{π x}{β})$
D $\frac{I_{0}}{4} {cos}^{2} (\frac{π x}{β})$
Question 2 - Select One
In a double slit experiment ,the separation between the slits is $d = 0.25 c m$ and the distance of the screen $D = 100$ cm from the slits .if the wavelength of light used in $λ = 6000 Å$ and $I_{0}$ is the intensity of the central bright fringe.the intensity at a distance $x = 4 \times 10^{- 5}$ in form the central maximum is-
A $I_{0}$
B $I_{0} / 2$
C $3 I_{0} / 4$
D $I_{0} / 3$
Question 3 - Select One
In Young's double-slit experiment $d / D = 10^{- 4}$ (d = distance between slits, D = distance of screen from the slits) At point P on the screen, resulting intensity is equal to the intensity due to the individual slit $I_{0}$ . Then, the distance of point P from the central maximum is $(λ = 6000 Å)$
A2 mm
B1 mm
C0.5 mm
D4 mm

CENGAGE PHYSICS-WAVE OPTICS-Single Correct

Home
Ask Doubt
Profile