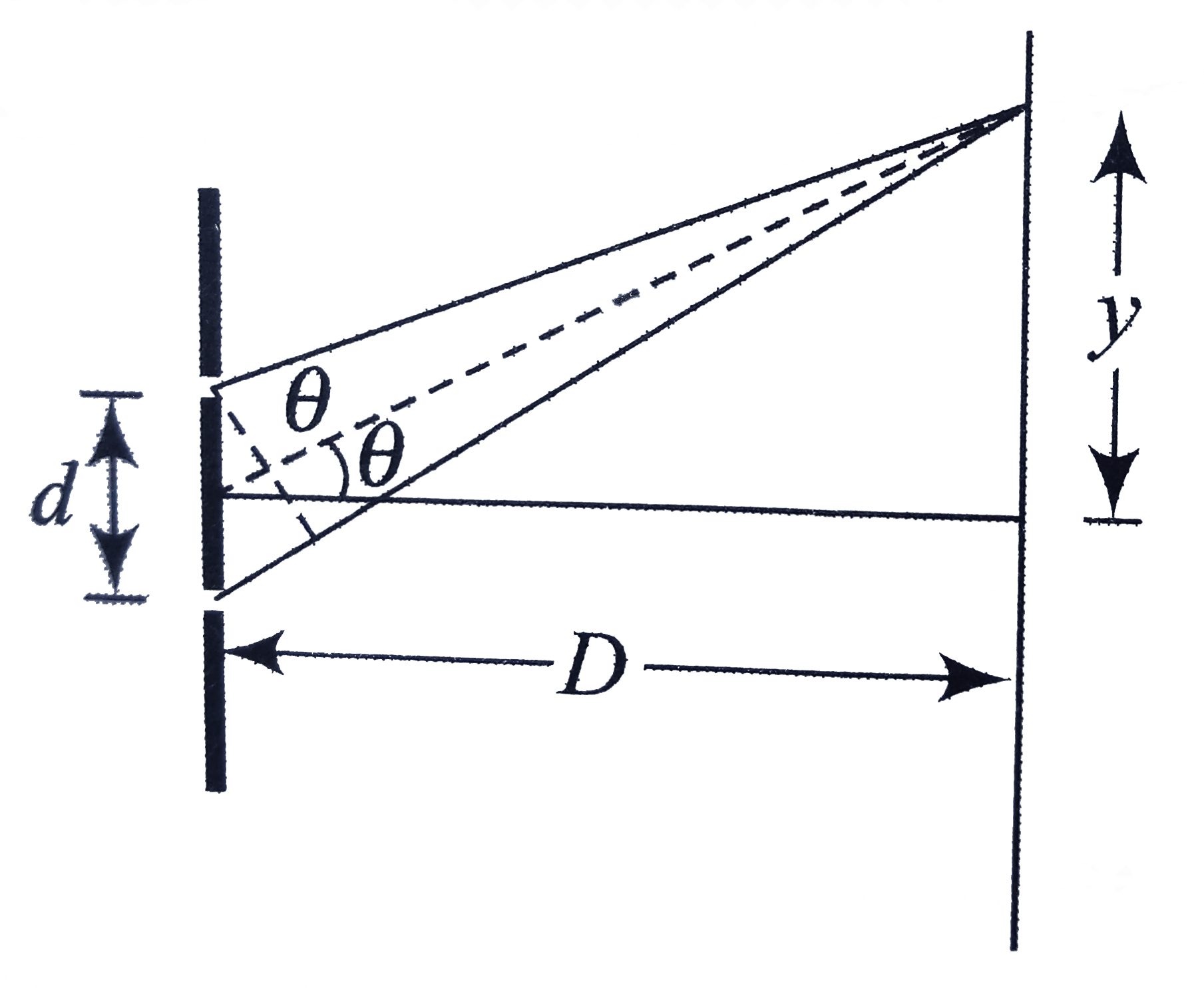
In an interference arrangement similar to Young's double-slit experiment, the slits S_1 and S_2 are illuminated with coherent microwave sources, each of frequency 10^6 Hz. The sources are synchronized to have zero phase difference. The slits are separated by a distance d=150.0 m. The intensity I (theta) is measured as a function of theta, where theta is defined as shown. If I_0 is the maximum intensity, then I (theta) for 0lethetale90degree is given by

I(θ)=I0/2 for θ=30∘
I(θ)=I0/4 for θ=90∘
I(θ)=I0 for θ=0∘
I(θ) is constant for all value of θ
The correct Answer is:c
We know that
I=I0cos2(δ2)
where
δ=2πλ×Dyd=2πtanθλ
I=I0cos2(πdtanθλ)
=I0cos2(π×150×tanθ3×108/106)
=I0cos2(π2tanθ)
For θ=30∘,I=I0cos252
For θ=90∘,I=I0cos2π/2=0
Hence, (c) is the correct option.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - MCQ
2 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Linked Comprehension type
5 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - True/False
2 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
In an interference arrangement similar to double-slit experiment, S1 and S2 are illuminated with coherent source microwave source each of frequency 1 MHz. the sources are synchronized to have zero phase difference . This slits are separated by distance d=150.0m The intensity I(θ) is measured as a funciton of θ, where θ is defined as shown in figure. If I0 is maximum intensity, calculate I(θ)
For :
a. θ=0 b. θ=30∘
c. θ=90∘
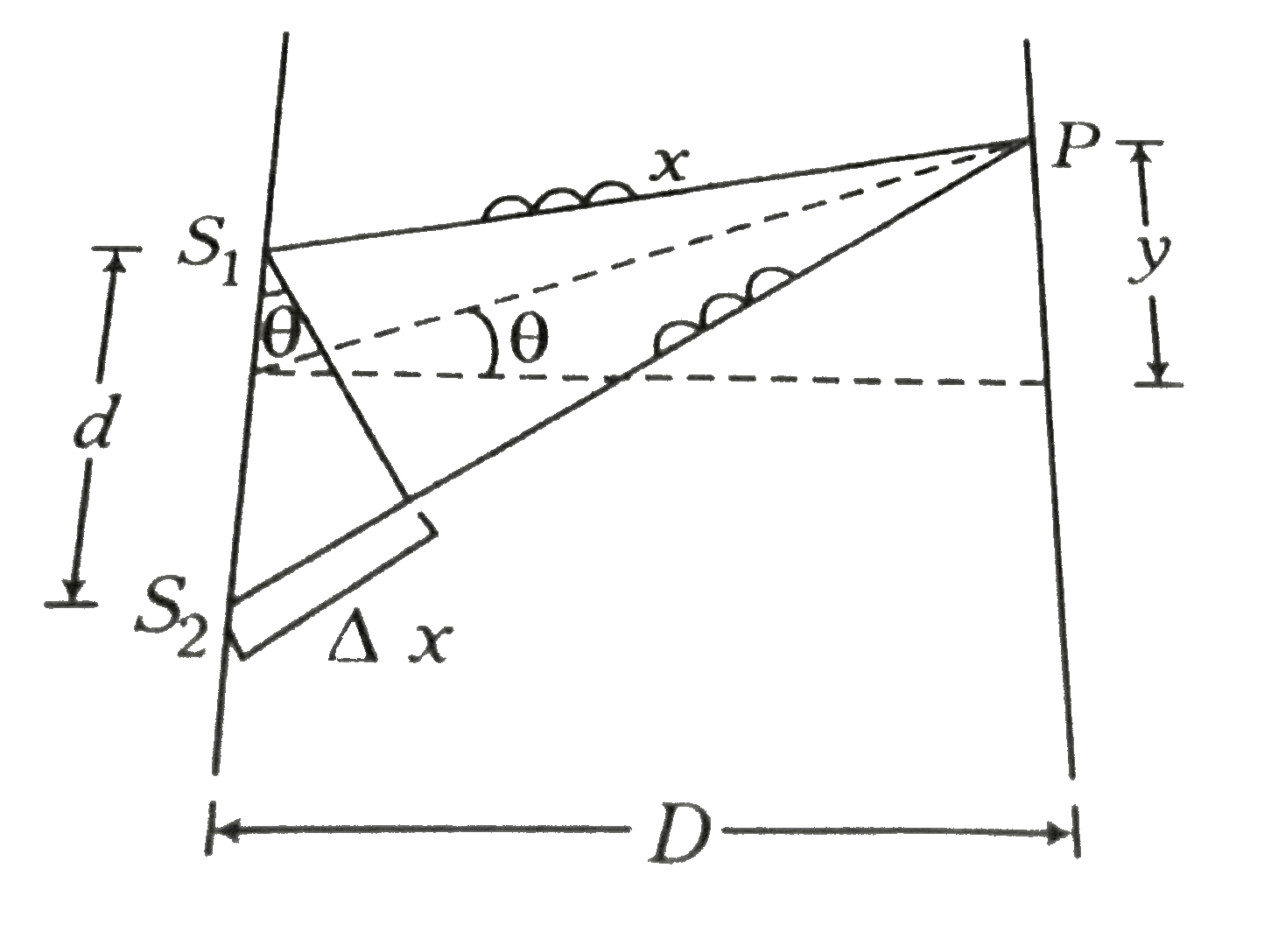
View SolutionConsider an interference arrangement similar to YDSE. Slits S1 and S2 are illuminated with coherent microwave sources each of frequency 2 MHz. The sources are synchronised to have zero phase difference. The slits are separated by distance d= 75m. The intensity I(θ) is measured as a function of θ where θ is defined as shown in figure. if I0 is maximum intensity then calculated I(θ) for (i)θ=0∘,(ii)θ=π/6and(iii)θ=π/2
View Solution
Knowledge Check
_E01_052_Q01.png)
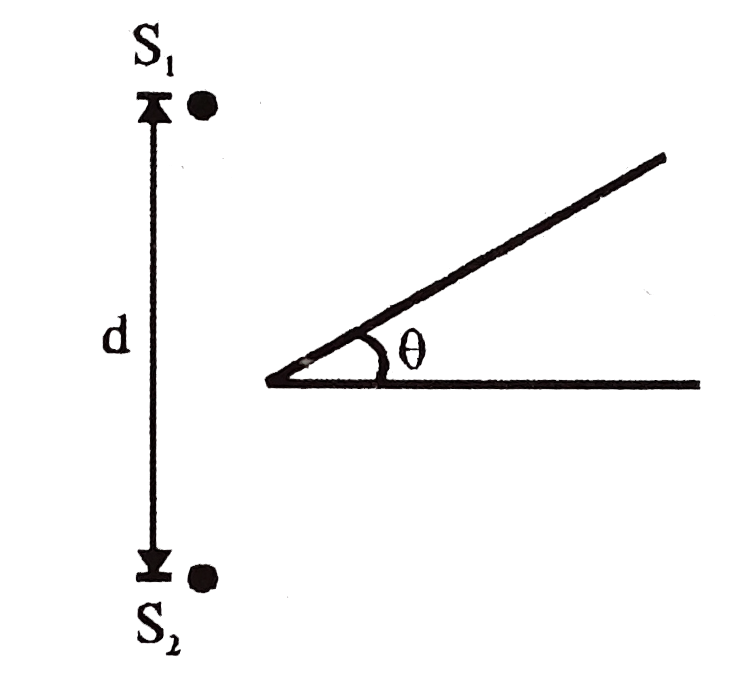
In an interference arrangement similar to young's double slit experiment the slits S1 and S2 are illuminated with coherent microwave sources each of frequency 106Hz the sources are synchronized to have zero phase difference. the slits are separated by a distance d=150.0m. The intensity I(θ) is measured as a funtion of θ, where θ is defined as shown. if I0 is the maximum intensity then I(θ) for 0≤θ≤90∘ is given by:AI(θ)=I0/2 for θ=30∘BI(θ)=I0/4 for θ=90∘CI(θ)=I0 for θ=0∘DI(θ) is constant for all values of θIn a interference arrangement similar to Young's double-slit experiment ,the slits S1 and S2 are illuminated with coheremt microwave source ,each of frequencies 106 Hz.The source are syhronized to have zero phase difference.The slits are separated by a distance from S1 and S2 where theta is defined as shown if I0 is the maximum intensity then
 AI(θ)=I02 for θ=30∘BI(θ)=I04 for θ=90∘CI(θ)=(I0) for θ=90∘DI(θ) is constant for all value of θ
AI(θ)=I02 for θ=30∘BI(θ)=I04 for θ=90∘CI(θ)=(I0) for θ=90∘DI(θ) is constant for all value of θIn Young's double slit experiment, if the two slits are illuminated with separate sources, no interference pattern is observed because
AThere will be no constant phase difference between the two wavesBThe wavelengths are not equalCThe amplitudes are not equalDNone of the above
In Young's double slit experiment, the intensity of central maximum is I. What will be the intensity at the same place if one slit is closed ?
View SolutionIn a Young’s double slit experiment, the source illuminating the slits is changed from blue to violet. The width of the fringes
View SolutionIn Young's double slit experiment, the ratio of maximum and minimum intensities in the fringe system is 9:1 the ratio of amplitudes of coherent sources is
View SolutionIn Youngsdoub≤slitexperiment,thephased⇔erentbetweentwocoherentsourcesofequal∫ensityisπ3.The∫ensityatap∮whichisatequaldistanceomthetwoslitsis(l_@) is maximum intensity)
View Solution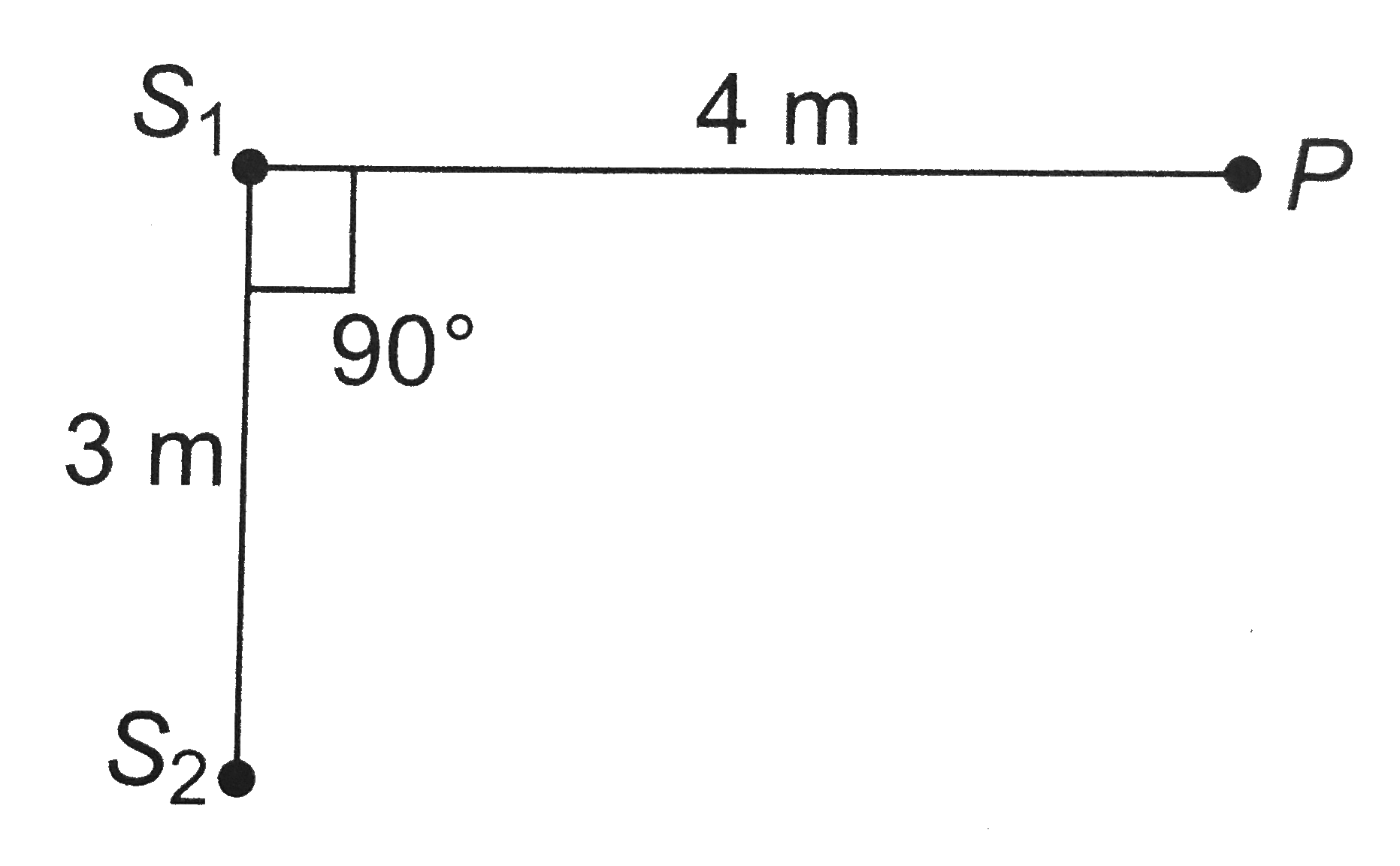
S1 and S2 are two coherent sources of sound of frequency 110Hz each they have no initial phase difference. The intensity at a point P due to S1 is I0 and due to S2 is 4I0. If the velocity of sound is 330m/s then the resultant intensity at P is
View Solution
