Question

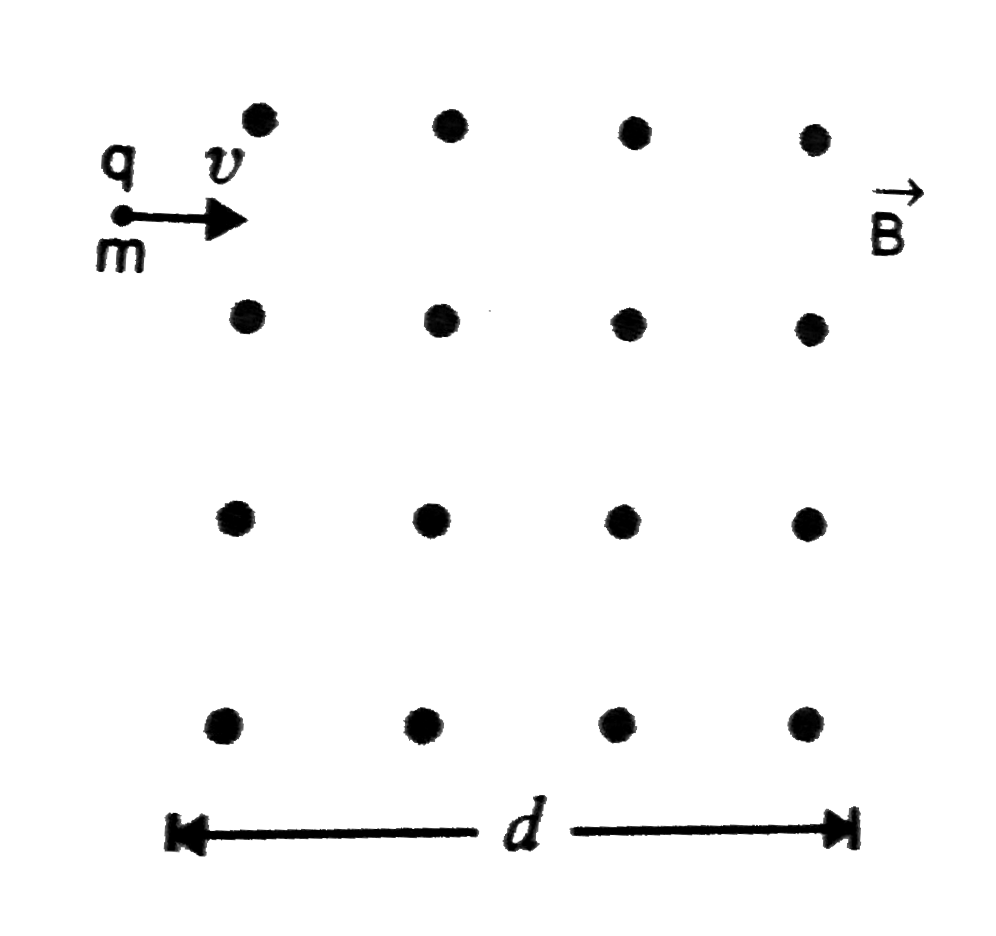
A particle with a specific charge s is fired with a speed v toward a wall at a distance d, perpendicular to the wall. What minimum magnetic field must exist in this region for the particle not to hit the wall?

Options

A. `v//sd`
B. `2v//sd`
C. `v//2sd`
D. `v//4sd`

Answer

a

Explanation

To solve the problem, we need to determine the minimum magnetic field required for a charged particle to move in a circular path without hitting the wall. Here’s a step-by-step solution:

Step 1: Understand the motion of the particle
When a charged particle moves in a magnetic field, it experiences a magnetic force that causes it to move in a circular path. The radius of this circular path is determined by the balance between the magnetic force and the centripetal force required to keep the particle in circular motion.

Hint: Recall the relationship between magnetic force, centripetal force, and radius in circular motion.

Step 2: Write down the equations for forces
The magnetic force \( F_B \) acting on the particle is given by:
\( F_B = qvB \)
where:
- \( q \) is the charge of the particle,
- \( v \) is the speed of the particle,
- \( B \) is the magnetic field strength.

The centripetal force \( F_C \) required to keep the particle moving in a circular path is given by:
\( F_C = \frac{mv^2}{r} \)
where:
- \( m \) is the mass of the particle,
- \( r \) is the radius of the circular path.

Hint: Set the magnetic force equal to the centripetal force for circular motion.

Step 3: Set the forces equal to each other
For the particle to not hit the wall, the magnetic force must equal the centripetal force:
\( qvB = \frac{mv^2}{r} \)

Hint: Rearrange the equation to solve for the magnetic field \( B \).

Step 4: Solve for the magnetic field \( B \)
Rearranging the equation gives:
\( B = \frac{mv}{qr} \)

Step 5: Relate the radius to the distance to the wall
In this scenario, the distance \( d \) to the wall is equal to the radius \( r \) of the circular path. Therefore, we can substitute \( r \) with \( d \):
\( B = \frac{mv}{qd} \)

Step 6: Substitute the specific charge
The specific charge \( s \) is defined as:
\( s = \frac{q}{m} \)
Thus, we can rewrite the magnetic field equation as:
\( B = \frac{v}{sd} \)

Final Answer
The minimum magnetic field \( B \) that must exist in this region for the particle not to hit the wall is:
\( B = \frac{v}{sd} \)