A proton is fired from origin with velocity $\to v = v_{0} ˆ j + v_{0} ˆ k$ in a uniform magnetic field $\to B = B_{0} ˆ j$ .

A

its z-coordinate can never be negative

B

its x-coordinate can never be negative

C

its x-and z-coordinates cannot be zero at the same time

D

its y-coordinate will be proportional to its time of flight

Video Solution

Text Solution

Verified by Experts

The correct Answer is:(b,d)

The path of the particle will be helix as shown in fig. Clearly
x-coordinate is always negative. z-coordinate can be negative
and positive both. X and z coordinate will be zero at the same
time at points A, C etc
$y = v_{0} t \Rightarrow y \propto t$

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

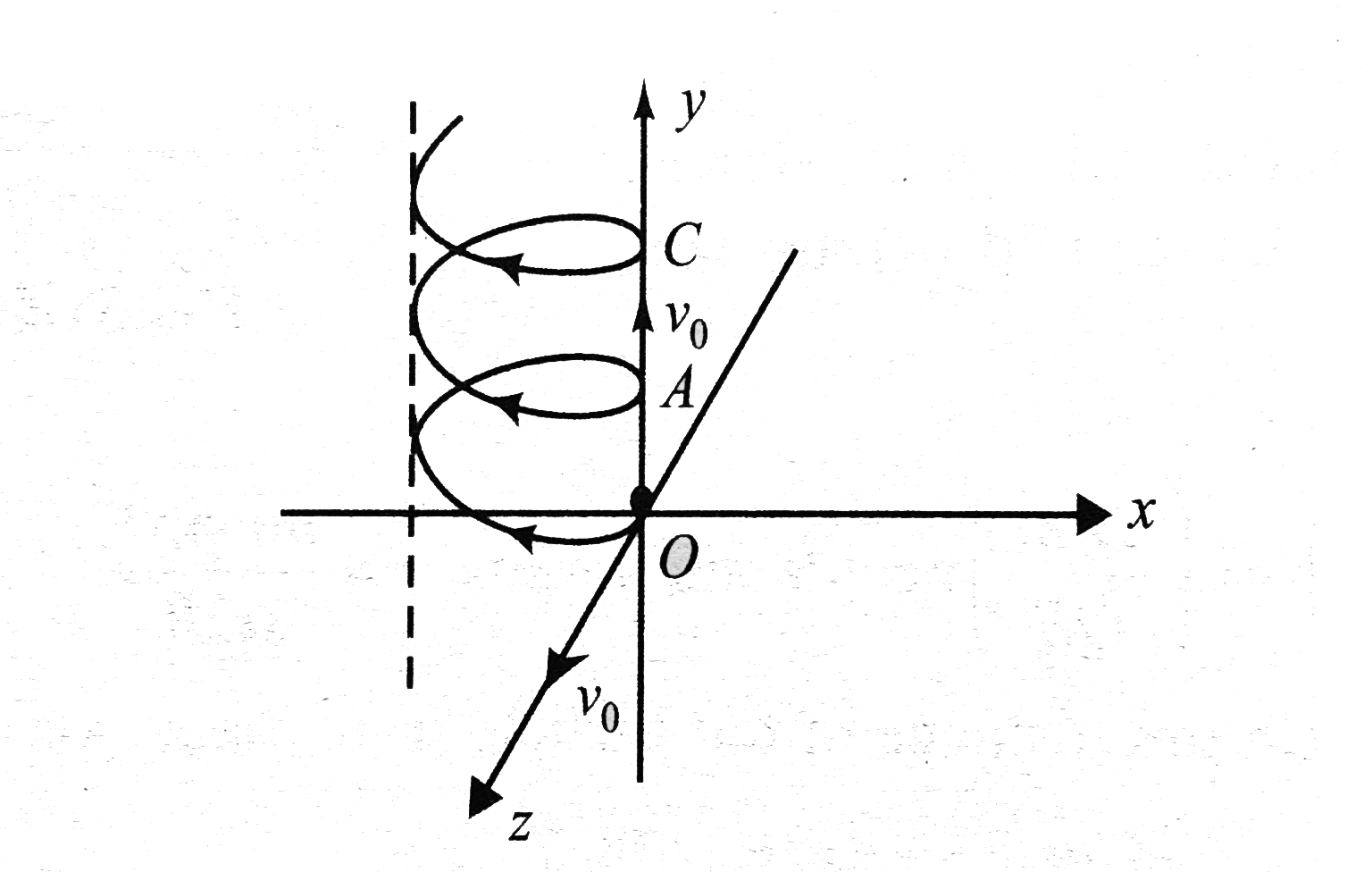
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
A portion is fired from origin with velocity $\to v = v_{0} ˆ j + v_{0} ˆ k$ in a uniform magnetic field $\to B = B_{0} ˆ j$ . In the subsequent motion of the proton
Aits z co-ordinate can never be negative
Bits x co-ordinate can never be positive
Cits x and z co-oridinate cannot be zero at the same time
Dits y co-ordinate will be proportional to its time of flight
Question 2 - Select One
A particle of charge per unit mass $α$ is released from origin with a velocity $\to v = v_{0} ˆ i$ uniform magnetic field $\to B = - B_{0} ˆ k$ . If the particle passes through $(0, y, 0)$ , then $y$ is equal to
A $- \frac{2 v_{0}}{B_{0} α}$
B $\frac{v_{0}}{B_{0} α}$
C $\frac{2 v_{0}}{B_{0} α}$
D $- \frac{v_{0}}{B_{0} α}$
Question 3 - Select One
A charged particle of specific charge (charge/mass) $α$ released from origin at time $t = 0$ with velocity $\to v = v_{0} (ˆ i + ˆ j)$ in uniform magnetic field $\to B = B_{0} ˆ i .$ Coordinates of the particle at time $t = π / (B_{0} α)$ are
A $(\frac{v_{0}}{2 B_{0} α}, \frac{\sqrt{2} v_{0}}{α B_{0}}, \frac{- v_{0}}{B_{0} α})$
B $(\frac{v_{0}}{2 B_{0} α}, 0, 0)$
C $(0, \frac{2 v_{0}}{B_{0} α}, \frac{v_{0} π}{2 B_{0} α})$
D $(\frac{v_{0} π}{B_{0} α}, 0, \frac{- 2 v_{0}}{B_{0} α})$

CENGAGE PHYSICS-MAGNETIC FIELD AND MAGNETIC FORCES-Exercises Multiple Correct

Home
Ask Doubt
Profile