A current I flows in a rectangularly shaped wire whose centre lies at (x0,0,0) and whose vertices are located at the points A (x0+d,−a,−b),B(x0−d,a,−b),C(x0−d,a,+b)andD(x0+d,−a,b) respectively. Assume that a,b,dltltx0. Find the magnitude of magnetic dipole moment vector of the rectangular wire frame in J/T. (Given, b=10 m,I=0.01A, d=4m,a=3m).
The correct Answer is:2
→m=I2→S
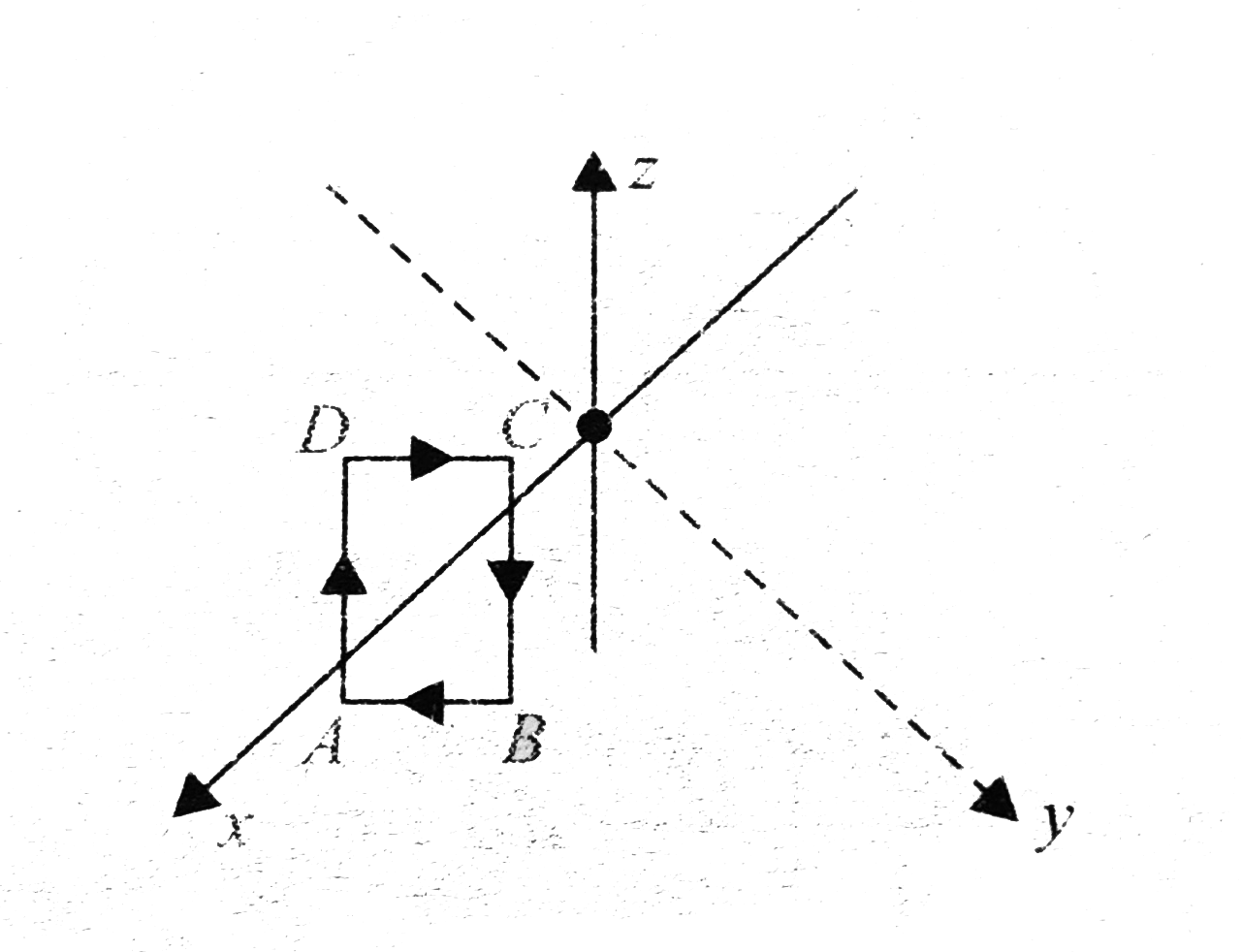
→S=−−→BA×−−→AD,−−→BA=2dˆi−2aˆj,−−→AD=2bˆk
→S=2(dˆi−aˆj)×2bˆk
→M=−4bI(dˆj+aˆi)⇒∣∣→M∣∣=4bI√d2+a2=2J/T
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Archives Fill In The Blank6videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Archives True /false4videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICSCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Linked Comprehension28videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank31videos
KINETIC THEORY
- BOOK - CENGAGE PHYSICSCHAPTER - Magnetism and MatterEXERCISE - Question Bank50videos
Magnetism and Matter
Similar Questions
A current I flows in a rectangularly shaped wire house centre lies at (x0,0,0) and whose vertices are located at the points A(x0+d,−a,−b),B(x0−d,a,−b),
C(x0−d,a,b) and
D(x0+d,−a,b) respectively. Assume that a,b,d<<x0 what is the magnitude of magnetic dipole vector of the rectangular wire frame in JT−1 (Given b=10m,d=12m,a=5m,I=0.03A)View SolutionFind the area of the quadrilateral whose vertices are A (0, 0), B (6, 0), C (4, 3) and D (0, 3).
View SolutionIf a<b<c<d, then the equation (x−a)(x−c)+2(x−b)(x−d)=0 has ( a) Imaginary roots (b) equal roots (c) distinct real roots (d) none of these
View SolutionIf the points (a,0),(b,0),(0,c), and (0,d) are concyclic (a,b,c,d>0), then prove that ab=cd.
View SolutionIf the point (x,4) lies on a circle whose centre is at the origin and radius is 5, then x= ±5 (b) ±3 (c) 0 (d) 14
View SolutionIf c,d are the roots of the equation (x−a)(x−b)−k=0 , prove that a, b are roots of the equation (x−c)(x−d)+k=0.
View SolutionIf a<b<c<d the equation (x−a)(x−c)+λ(x−b)(x−d)=0 has real roots for
View SolutionIf a≠0andlogx(a2+1)<0 then x lies in the interval (A) (0,∞) (B) (0,1) (C) (0,a) (D) none of these
View SolutionIf c,d are the roots of the equation (x−a)(x−b)−k=0 , prove that a, b are roots of the equation (x−c)(x−d)+k=0.
View SolutionThe equation of the tangent to the curve y=secx at the point (0,1) is
(a) y=0
(b) x=0
(c) y=1
(d) x=1View Solution

