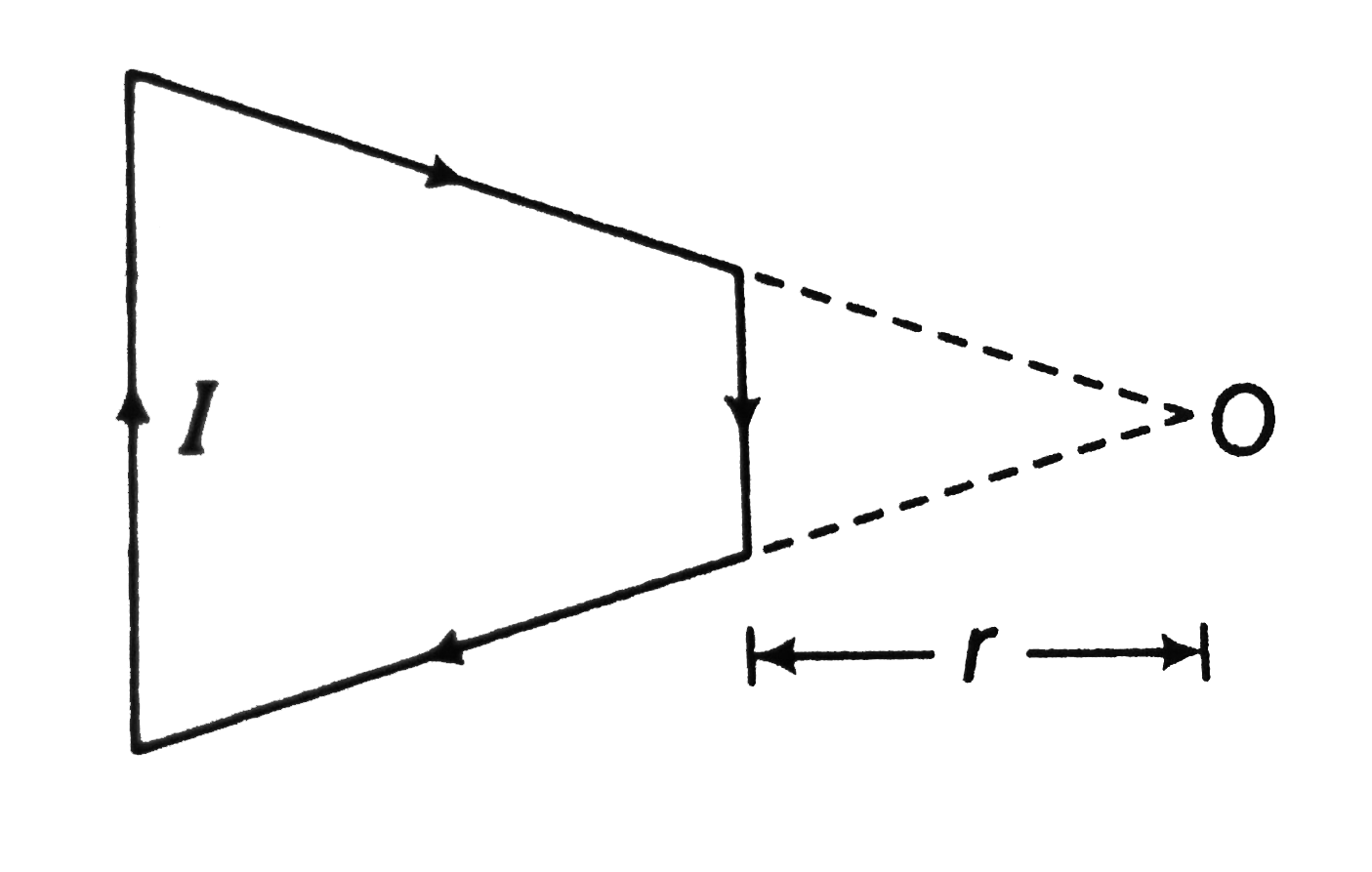
A current I flows in a circuit shaped like an isosceles trapizium. The ratio of the bases is 2. The length of the smaller base is l. Calculate the megnetic field induction at point P located in the plane of the trapizium, but at a distance a from the midpoint of the smaller base,

Video Solution

Text Solution

Verified by Experts

From similar triangles APF and CPE, we find $d = 2 a$ and
$tan α = \frac{1}{2 a}$ . Magnetic field at P due to wire 1 is
$B_{1} = \frac{μ_{0} I}{4 π d} [sin α - sin (- α)] = \frac{μ_{0} I sin α}{2 π d} = \frac{μ_{0} I sin α}{4 π a}$
The direction of the magnetic field is into the plane of the paper.
$α$ is the half-angle subtended by the wire 1 at point P and d is the
perpendicular distance between the wire and point P.

Magnetic field at P due to wires (2) and (4) is zero.
Megnetic field at P due to wire 3 is
$B = B_{3} - B_{1} = \frac{μ_{0} I sin α}{2 π a} - \frac{μ_{0} I sin α}{4 π a} = \frac{μ_{0} I sin α}{4 π a}$
or $B = \frac{μ_{0} I}{4 π a} [\frac{1}{\sqrt{l^{2} + 4 a^{2}}}]$
out of the plane of the paper.

Updated on:21/07/2023