A rod of length l, has a uniform positive charge per unit length and a total charge Q. calculate the electric foeld at a point P located along the long axis of the rod and at a distance a from one end

The field d→E at P due to each segment of charge on the rod is in the negative x direction because every segment carries a positive charge.
Because the rod is continous we are evaluating the field due to a continuous charge distribution rather than a group of individual charges. Because every segment of the negative x direction, the sum of their contributions can be handled without the need to add vectors.
Let us assume the rod is lying along the x-axis , dx is the length of one small segment and dq is the charge on that segment. Beacuse the rod has a charge per unt length 1, the charge dq on the small segment is dq=λdx. The magnitude of the electric field at P due to one segment of the rod having a charge dq is
dE=kedqx2=keλdxx2
The total field at P is
E=∫l+aaKeλdxx2
If Ke and λ=Q/l are constants and can be removed from the integral, them
E=∫l+aakeλdxx2[−1x]l+aa
=keQl(1a−1l+a)=keQa(l+a)
If a to b, which corresponds to sliding the bar to the left until its left end is at the origin, then E→∞ that represents the condition in wich the observation point P is at zero distance from the charge at the end of the rod, so the field become infinite.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Solved examples10videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Exercises58videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - COMMUNICATION SYSTEMEXERCISE - QUESTION BANK19videos
COMMUNICATION SYSTEM
- BOOK - CENGAGE PHYSICSCHAPTER - Current ElectricityEXERCISE - QUESTION BANK40videos
Current Electricity
Similar Questions
A rod length l is uniformly charged with charge q. Calculate potential at point P.
 View Solution
View SolutionFigure 22-24 shows a plastic rod having a uniformly distributed charge. The charge per unit length of the rod is λ. Find the electric field due to the rod at a point P which is at a distance r from the rod.
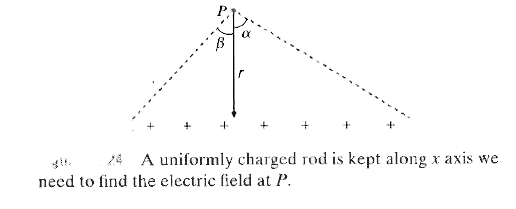 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A cylinder of length L has a charge of magnitude q. The electric intensity at a point at a distance r from the axis of the cylinder is
AE=14π∈0K⋅qr2BE=12π∈0k⋅qrLCE=σ/∈0kDnone of these - Question 2 - Select One
A solid cyclindrical insulator of uniform density having length 4 and radius 2 contains charge Q. Find the value of the electric field at a distance L along the axis from one end. (L=length of insulator)
AQ16πε0(2−√17)BQ32πε0(2+√5)CQ16πε0(√5−√17)DQ16πε0(2−√17−√5) - Question 3 - Select One
The electric field at a distance r from a long wire having charge per unit length λ is
Ak(λr2)Bk(λr)Ck(λ2r)Dk(2λr)
A thin straight rod of length 2a carrying a uniformly distributed charge q is located in vacumm. Find the magnitude of the electric field strength as a function of the distatance r from the rod's centre along the streaight line
(a) perpendicular to the rod and passing through its centre ,
(b) coinciding with the rod's direction (at the point lying outside the rod).View SolutionThe moment of inertia of a thin rod of mass M and length L about an axis perpendicular to the rod at a distance L/4 from one end is
View SolutionA thin straight rod of length l carrying a uniformly distributed charge q is located in vacuum. Find the magnitude of the electric force on a point charge 'Q' kept as shown in the figure.
 View Solution
View SolutionA massless rod of length L has two equal charges (q) tied to its ends. The rod is free to rotate in horizontal plane about a vertical axis passing through a point at a distance L4 from one of its ends. A uniform horizontal electric field (E) exists in the region. (a) Draw diagrams showing the stable and unstable equilibrium positions of the rod in the field. (b) Calculate the change in electric potential energy of the rod when it is rotated by an angle Δθ from its stable equilibrium position. (c) Calculate the time period of small oscillations of the rod about its stable equilibrium position. Take the mass of each charge to be m.
View SolutionA 10 cm long rod carries a charge of +150μC distributed uniformly along its length. Find the magnitude of the electric field at a point 10 cm from both the ends of the rod.
View Solution

