A wire is bent into the shape shown in fig and the magnetic field is measured at $P_{1}$ when the current in the wire is I. The same wire is then formed into the shape shown in the Fig and the magnetic field is measured at point $P_{2}$ when the current is again I. If the total length of wire is the same in each case, what is the ratio of $B_{1} / B_{2}$ ?

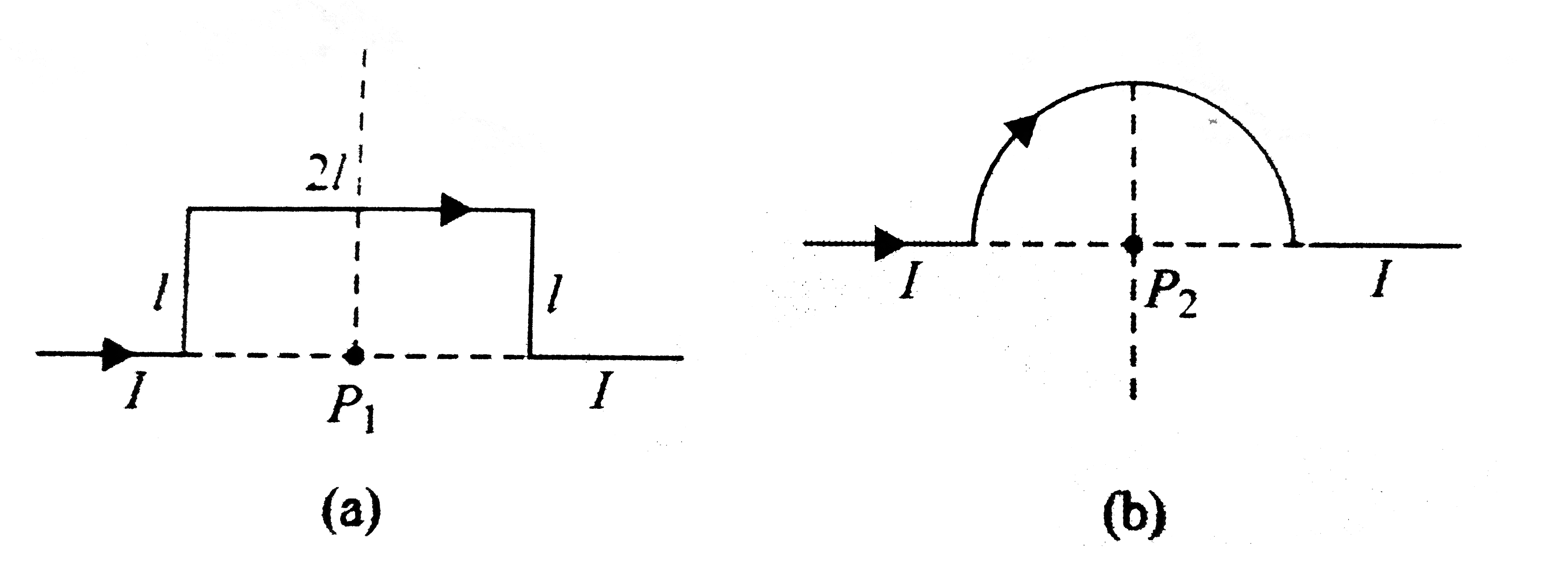
Video Solution

Text Solution

Verified by Experts

Case I: ${\to B}_{net} = {\to B}_{1} + {\to B}_{2} + {\to B}_{3}$
$= [\frac{μ_{0} I}{4 π l} [0 + {sin 45}^{\circ}] + \frac{μ_{0} I}{4 π l} [{sin 45}^{\circ} + {sin 45}^{\circ}]$
$+ \frac{μ_{0} I}{4 π l} [0 + {sin 45}^{\circ}]] \otimes$

$∴ ∣ ∣ {\to B}_{net} ∣ ∣ = \frac{μ_{0} I}{\sqrt{2} π l} = B_{1}$
CaseII: $2 π r = 4 l \Rightarrow \frac{2 l}{π}$
Magnetic field at the centre of semicircle,
$B_{semicircle} = \frac{μ_{0} I}{4 r} = \frac{μ_{0} I π}{8 l} = B_{2}$
$\frac{B_{1}}{B_{2}} = \frac{μ_{0} I}{\sqrt{2} π l} \times \frac{8 l}{μ_{0} I π} = \frac{4 \sqrt{2}}{π^{2}}$ .

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is

A $\frac{μ_{0} I}{4 π R} \sqrt{1 + π^{2}}$
B $\frac{μ_{0} I}{4 π R} \sqrt{2 + π^{2}}$
C $\frac{μ_{0} I}{4 π R} \sqrt{4 + π^{2}}$
D $\frac{μ_{0} I}{4 π R} \sqrt{9 + π^{2}}$
Question 2 - Select One
The magnetic field at O due to current in the infinite wire forming a loop as a shown in Fig.

A $\frac{μ_{0} I}{2 π d} ({cos ϕ}_{1} + {cos ϕ}_{2})$
B $\frac{μ_{0}}{4 π} \frac{2 I}{d} ({tan θ}_{1} + {tan θ}_{2})$
C $\frac{μ_{0}}{4 π} \frac{I}{d} ({sin ϕ}_{1} + {sin ϕ}_{2})$
D $\frac{μ_{0}}{4 π} \frac{I}{d} ({cos θ}_{1} + {cos θ}_{2})$
Question 3 - Select One
For the current carrying wire, show that the magnetic field at P is

A $\frac{μ_{0} i}{4 π} (\frac{3 π}{2 R} + \frac{\sqrt{2}}{d}) ⊙$
B $\frac{μ_{0} i}{4 π} (\frac{3 π}{2 R} - \frac{\sqrt{2}}{d}) \otimes$
C $\frac{μ_{0} i}{4 π} (\frac{3 π}{2 R} - \frac{\sqrt{2}}{d}) ⊙$
D $\frac{μ_{0} i}{4 π} (\frac{3 π}{2 R} + \frac{\sqrt{2}}{d}) \otimes$

CENGAGE PHYSICS-SOURCES OF MAGNETIC FIELD-Concept Exercise 2.1

Home
Ask Doubt
Profile