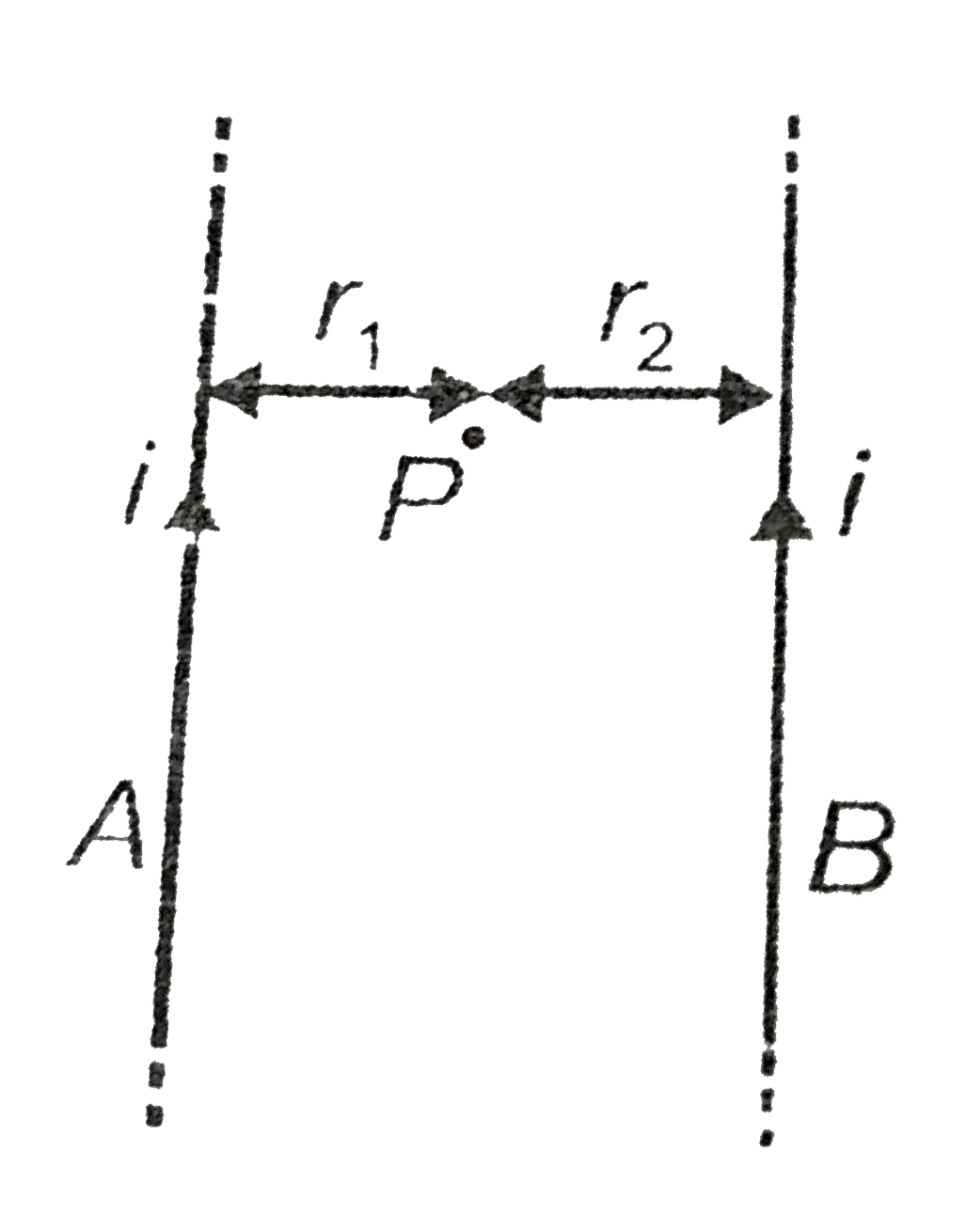
The magnetic field at O due to current in the infinite wire forming a loop as a shown in Fig.

μ0I2πd(cosϕ1+cosϕ2)
μ04π2Id(tanθ1+tanθ2)
μ04πId(sinϕ1+sinϕ2)
μ04πId(cosθ1+cosθ2)
The correct Answer is:A
(a) Using B=μ0i4πa[sinθ1+sinθ2]
But θ1+ϕ1=90∘orθ1=90∘−ϕ,
sinθ1=sin(90∘−ϕ1)=cosϕ1
Similarly, sinθ2=cosϕ2
Bnet=μ0I2πa(cosϕ1+cosϕ2)
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (multiple Currect )
5 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (assertion-reasioning )
2 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )
10 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank
40 Videos
Similar Questions
Knowledge Check
The magnetic field at the origin due to the current flowing in the wire is
 A−μ0I8πa(ˆi+ˆk)Bμ0I2πa(ˆi+ˆk)Cμ0I8πa(−ˆi+ˆk)D−μ0I4πa√2(ˆi−ˆk)
A−μ0I8πa(ˆi+ˆk)Bμ0I2πa(ˆi+ˆk)Cμ0I8πa(−ˆi+ˆk)D−μ0I4πa√2(ˆi−ˆk)Net magnetic field at the centre of the circle O due to a currying loop as shown in figure is (θ<180∘)
 .AzeroBperpendicular to paper inwardsCperpendicular to paper outwardsDis perpendicular to paper inwards if θ≤90∘ and perpendicular to paper outward of 90∘≤θ<180∘ .
.AzeroBperpendicular to paper inwardsCperpendicular to paper outwardsDis perpendicular to paper inwards if θ≤90∘ and perpendicular to paper outward of 90∘≤θ<180∘ .Magnetic field produced at the point O due to current flowing in an infinite wire shaped as shown in the figure is
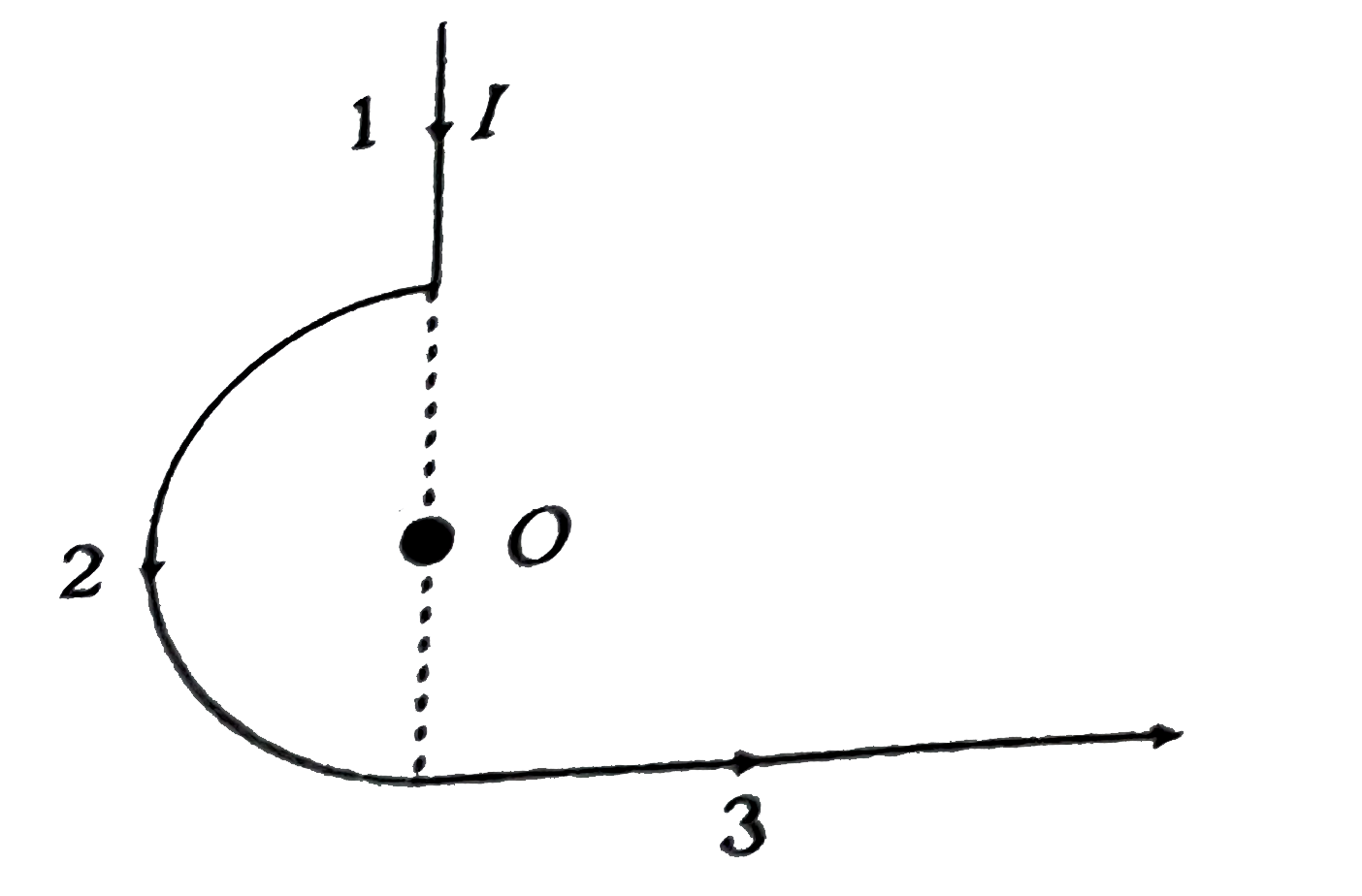 Aμ0I4πRBμ0I4R−μ0I4πRCμ0I4R−μ0I2πRDμ0I4R+μ0I4πR
Aμ0I4πRBμ0I4R−μ0I4πRCμ0I4R−μ0I2πRDμ0I4R+μ0I4πR
Find the magnetic field at the origin due to the combination of two semi infinite wires and a semicircular wire as shown.

View SolutionA current circular conducting loop exerts a magnetic field both inside and outside it. The magnetic field at the cetre of a current loop of radius 'R' and carrying a current I is given as :
B=μ0I2R
The magnetic field lines due to a circular current loop form closed loops. The direction of the magnetic field is given by the right hand thumb rule, which states that if one curls the palm of his right hand around the current loop with the fingers pointing in the direction of the current, the right hand thumb will give the direction of the magnetic field. From this law it is clear that the direction of magnetic field →B is always perpendicular to the direction of flow of current or perpendicular to the plane of circular current loop.

How is the magnetic field at O modified when the two loops are rearranged as shown in Fig.
View SolutionThe magnetic field at the centre of the circular loop as shown in Fig. when a single wire is bent to form a circular loop and also extends to form straight sections is
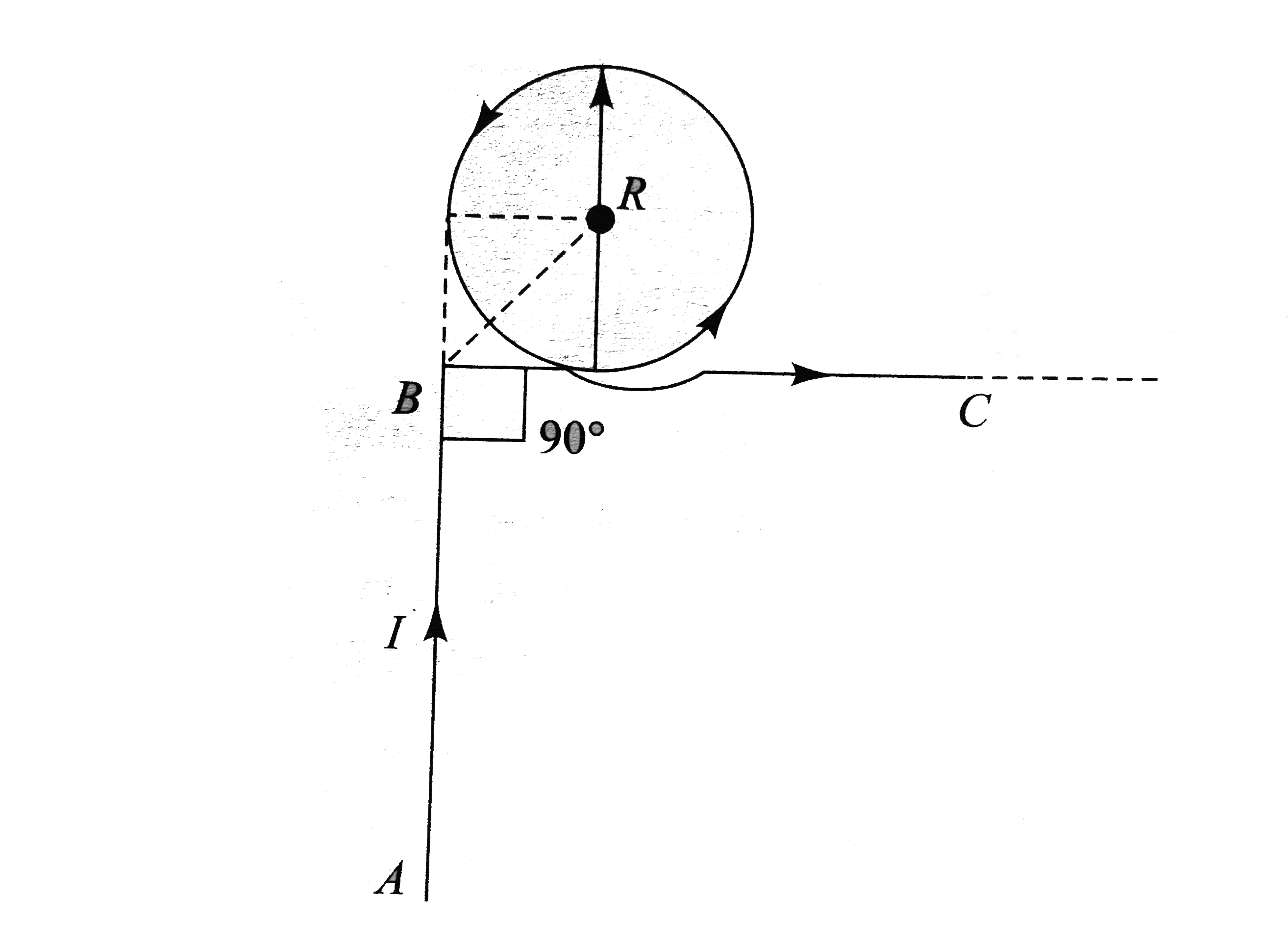
View SolutionNet magnetic fields at the centre of the circles O due to a current carrying loop as show in figure is (θ<180∘)

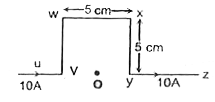
View SolutionThe resulting magnetic field at the point O due to the current carrying wire shown in the figure:
View Solution