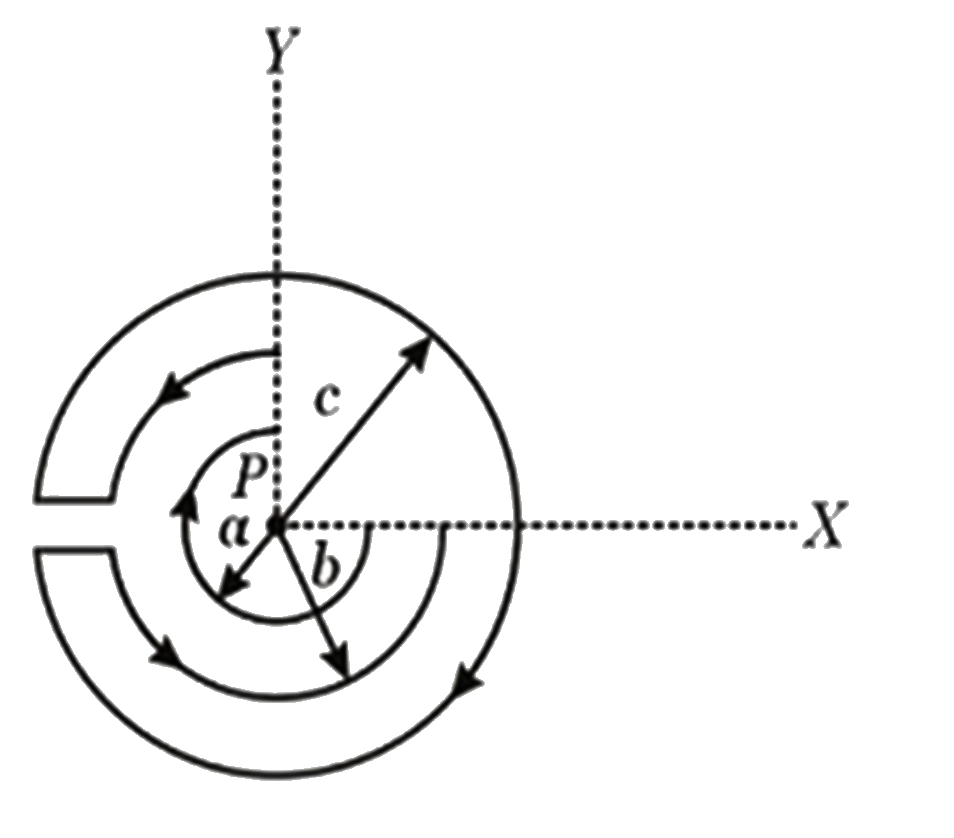
For c=2a if, the magnetic field at point P will be zero when

a=b
a=35b
a=53b
a=13b
The correct Answer is:C
(c) Magnetic field at the centre
B=μ0I2c⊗+μ0I2b(34)⊙+μ0I2a(34)⊗
As per problem:
0=μ0I2[1c−34b+34a]⇒34[1b−1a]=1c
If c=2a,
34[1b−1a]=12a⇒a=53b
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (multiple Currect )5videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (assertion-reasioning )2videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )10videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK12videos
SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank40videos
THERMAL PROPERTIES OF MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
For c=2aandc<b<c, the magnetic field at the point P will be zero when-
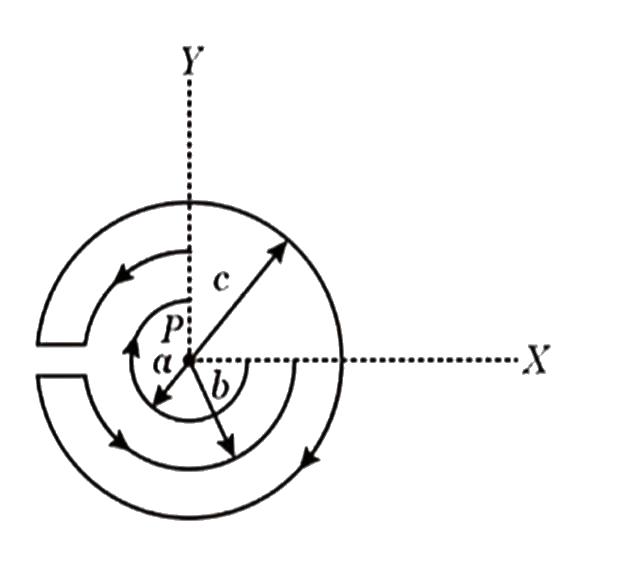 Aa=bBa=35 bCa=53bDa=13b
Aa=bBa=35 bCa=53bDa=13b - Question 2 - Select One
The magnetic field at centre , P will be
 Aμ04πBμ0πCμ02πD4μ0π
Aμ04πBμ0πCμ02πD4μ0π - Question 3 - Select One
Refer to figure, where c=3a and a<b<c, the magnetic field induction at point O will be zero due to current I in the various portion of the network when
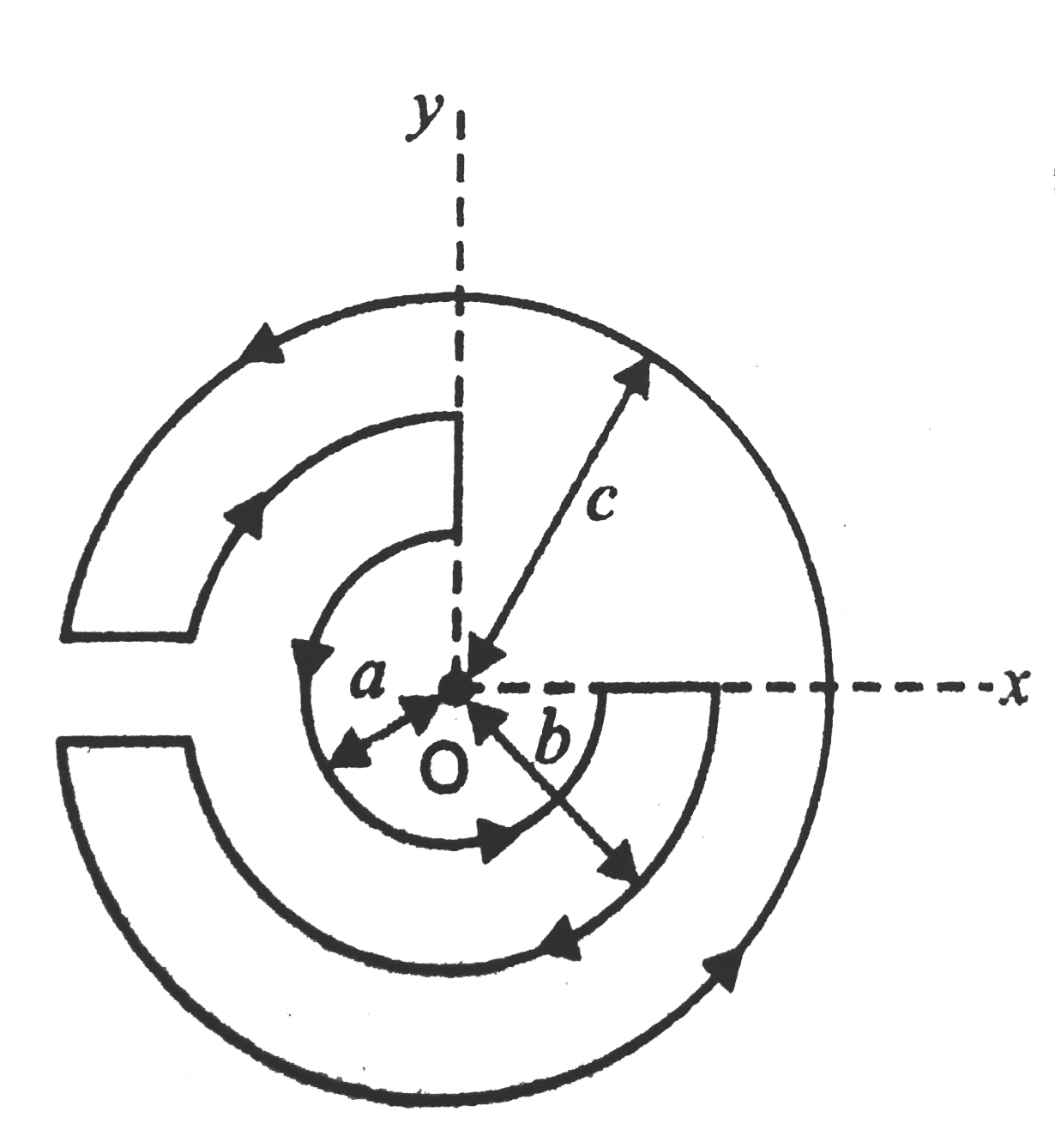 Ab=57aBb=7a9Cb=9a13Db=13a15
Ab=57aBb=7a9Cb=9a13Db=13a15
For adjoining fig, The magnetic field at point, 'P' will be:
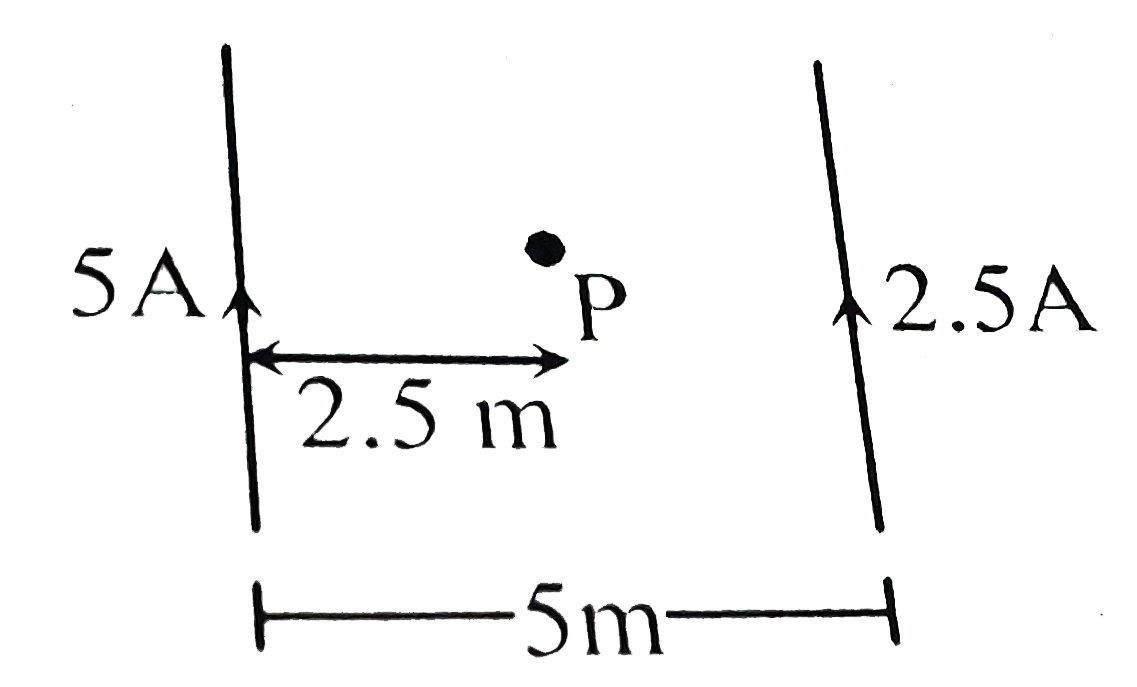 View Solution
View SolutionFind the magnetic field at point P in following cases
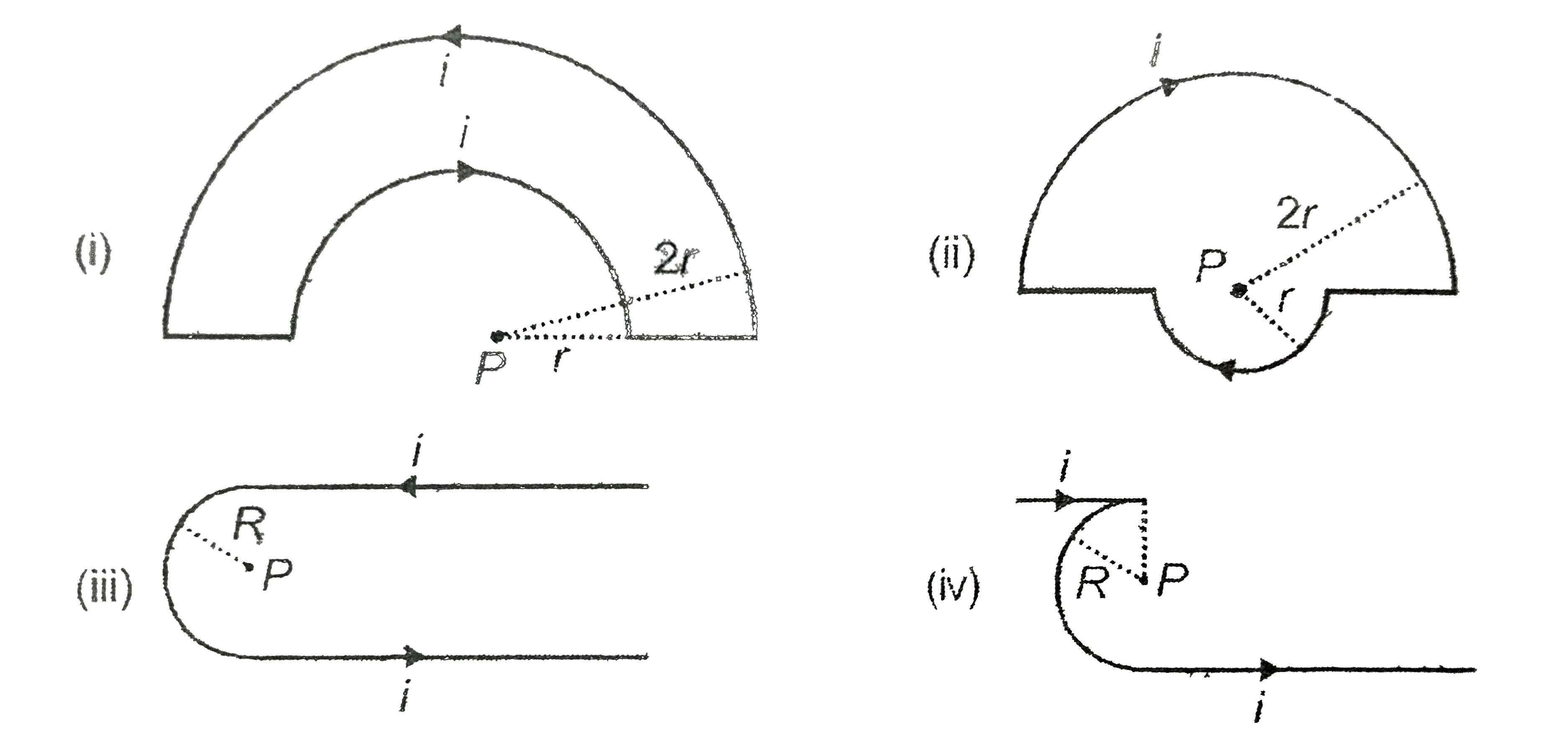 View Solution
View SolutionFind the magnetic field B at the point P in figure
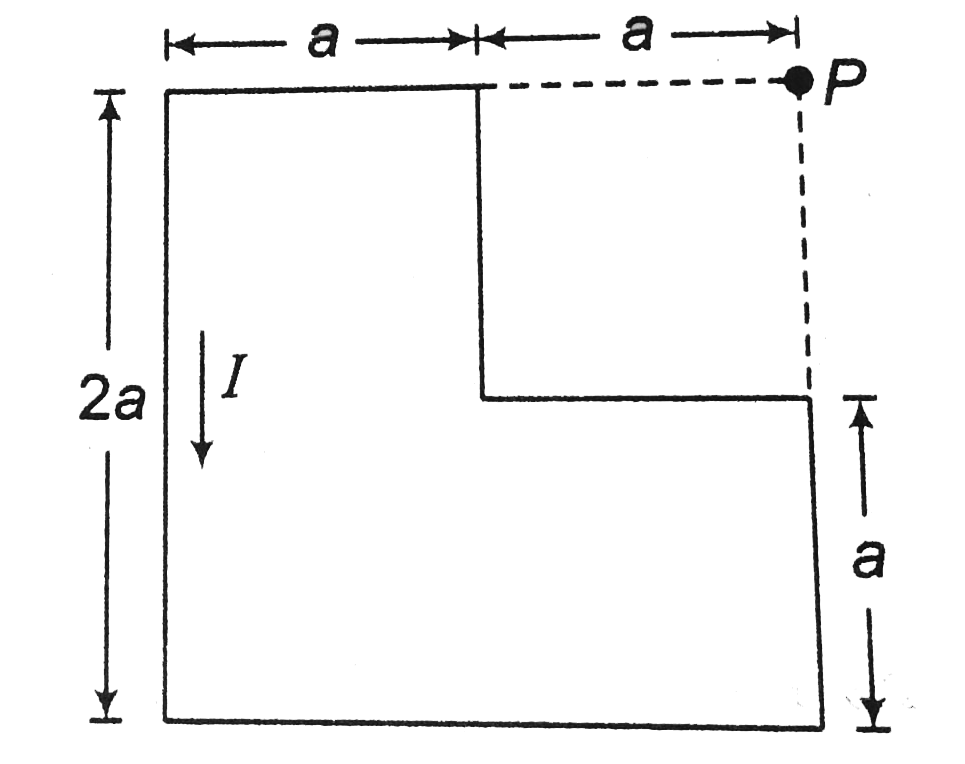 View Solution
View SolutionA cell is connected across two points P and Q of a uniform circular conductor, figure. Prove that the magnetic field at its centre O will be zero.
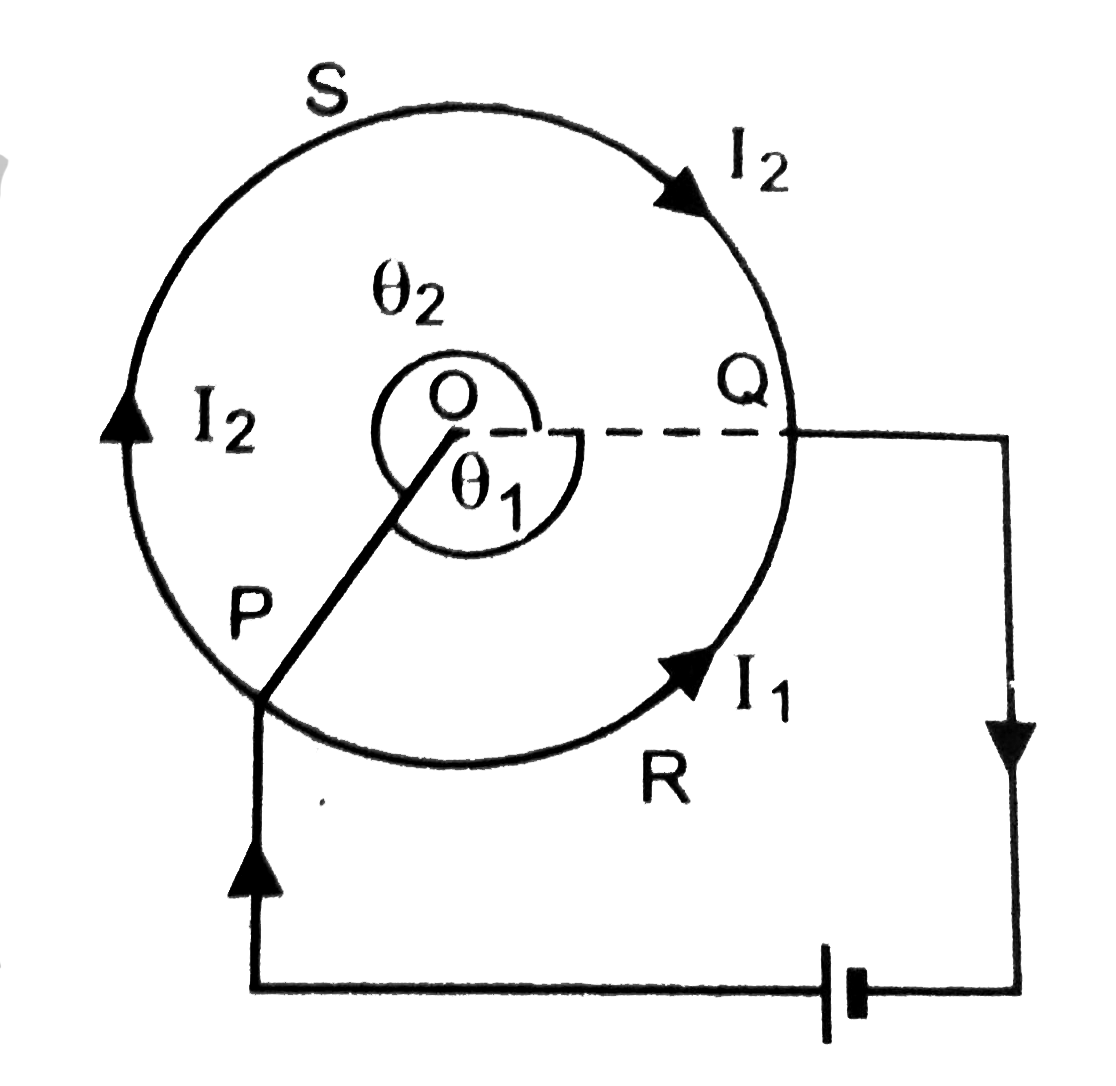 View Solution
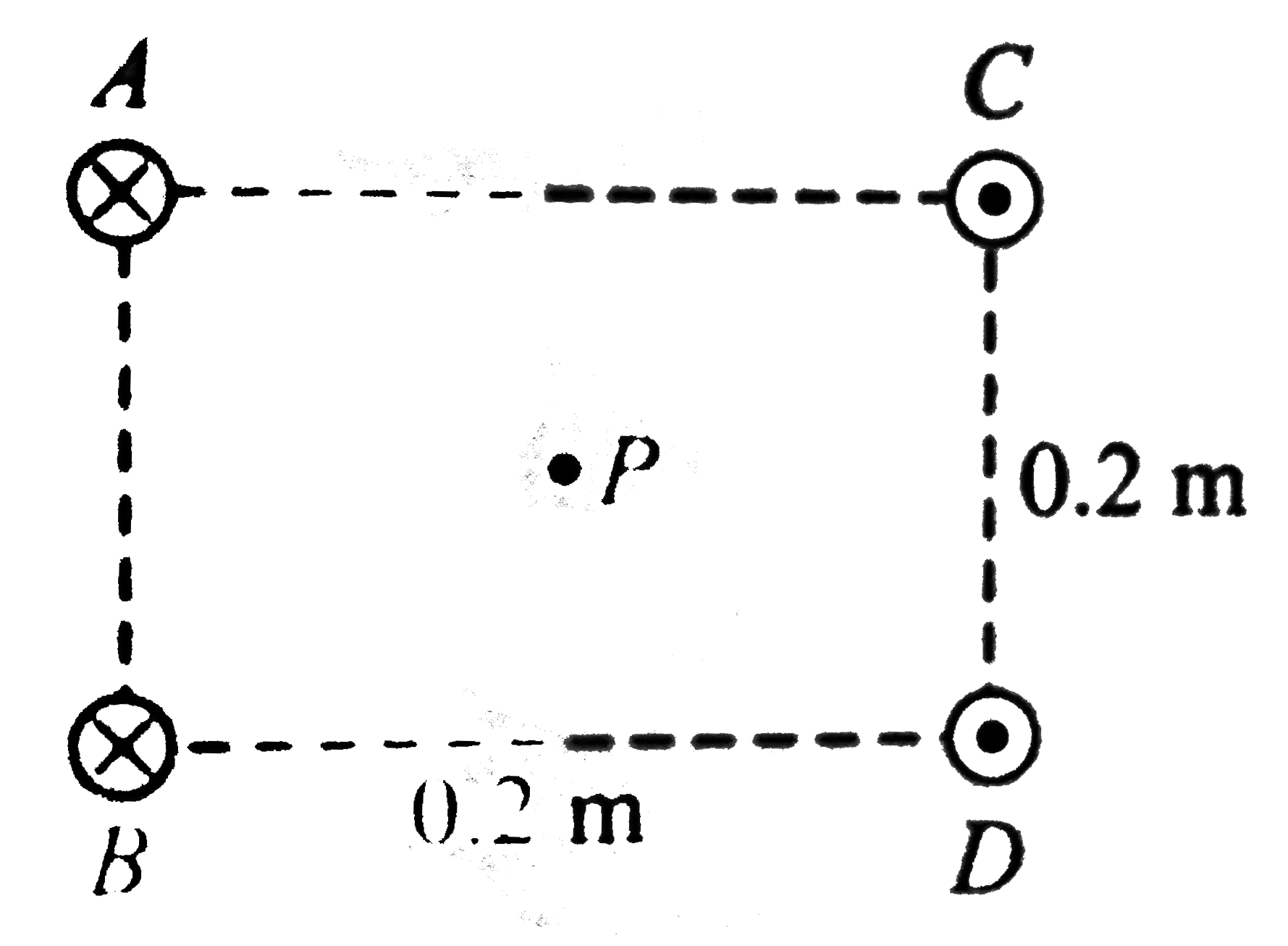
View SolutionFour long, parallel conductors carry equal currents of 5.0A. The direction of the currents is into the page at point A and B and out of the page at C and D. Calculate the magnetic and direction of the magnetic field at point P, located at the centre of the square.
 View Solution
View Solution