For c = 2 a and a<b<c , the magnetic field at the point P will be zero when
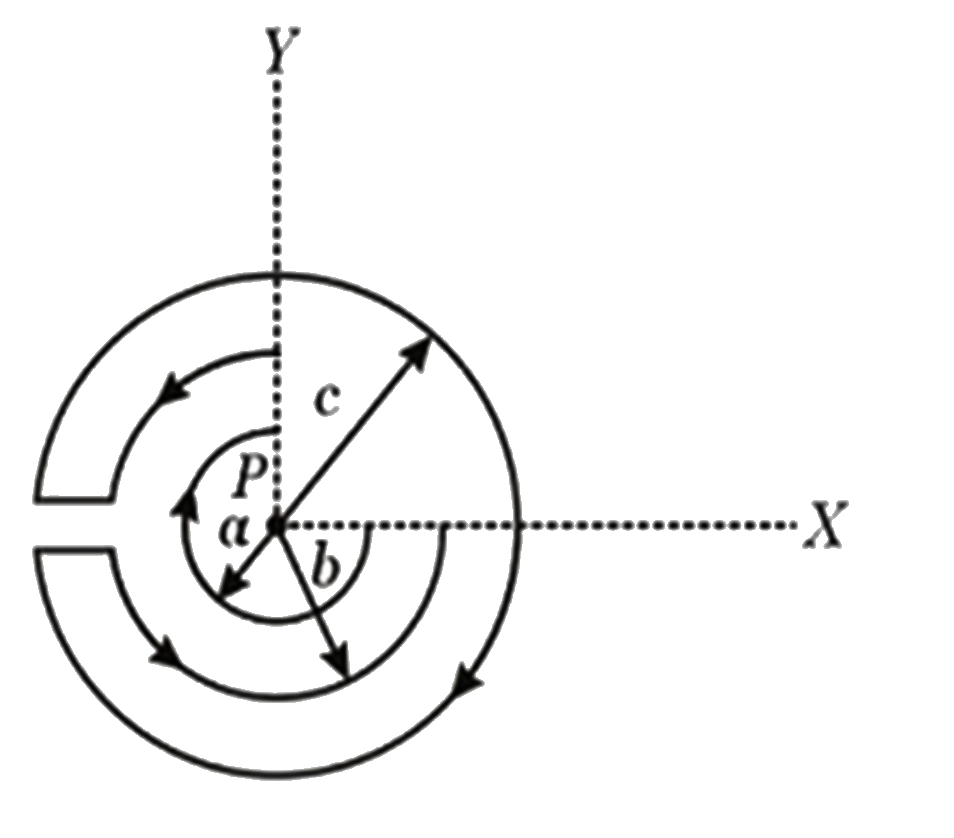
a = b
a=35b
a=53b
a=13b
The correct Answer is:C
Step by step video & image solution for For c = 2 a and a lt b lt c , the magnetic field at the point P will be zero when by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
There are two co-axial non conducting cylinders of radii a and b(>a). Length of each cylinder is L(>>b) and their curved surfaces have uniform surface charge densities of–σ (on cylinder of radius a) and +σ (on cylinder of radius b). The two cylinders are made to rotate with same angular velocity ω as shown in the figure. The charge distribution does not change due to rotation. Find the electric field (E) and magnetic field (B) at a point (P) which is at a distance r from the axis such that (a) 0<r<a (b) a<r<b (c) r>b. Assume that point P is close to perpendicular bisector of the length of the cylinders
View SolutionIf the median of a, b, c, d, e, and f (a<b<c<d<e<f) then the median of b, c, d, and e is________
View Solution
Knowledge Check
- Question 1 - Select One
For c=2aandc<b<c, the magnetic field at the point P will be zero when-
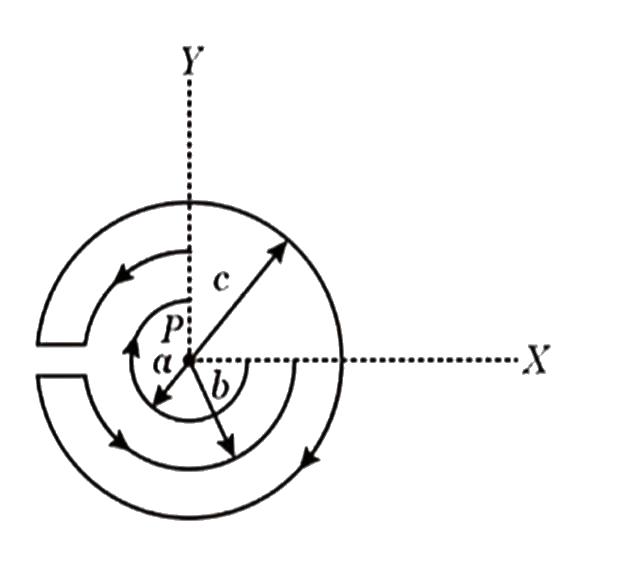Aa=bBa=35 bCa=53bDa=13b - Question 2 - Select One
For c=2a if, the magnetic field at point P will be zero when
Aa=bBa=35bCa=53bDa=13b - Question 3 - Select One
If three successive positive integers a,b,c are such that a<b<c, then which of the following options will be correct?
Aa+ba+b+c>b+ca+b+c>c+aa+b+cBc+aa+b+c>b+ca+b+c>a+ba+b+cCb+ca+b+c>c+aa+b+c>a+ba+b+cDb+ca+b+c>a+ba+b+c>c+aa+b+c
If ax2+bx+c=0,a,b,c∈ R has no real roots, and if c< 0, the which of the following is ture ? (a) a< 0 (b) a + b + c > 0 (c) a+b+c< 0
View SolutionIf a<0,b>0and c<0, then the point P(a,b,−c) lies in the octant
View SolutionIf a , b, c, d are non-zero integers such that a<b<c<d and median of a, b, c are both equal to zero, then which one of the following is correct?
View SolutionIf the median of a, b, c, d, and e(a<b<c<d<e) is k, then find the median of b2,c2,andd2.
View SolutionA magnetic field →B=B0ˆj exists in the region a<x<2a and →B=−B0ˆi in the region 2a<x<3a, where B0 is positive constant. A positive point charge moving with a velocity →v=v0ˆi where v0 is a positive constant, enters.
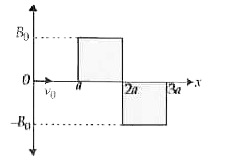
the magnetic field at x=a, The trajectory of the charge in this region can be like,View Solution