State Biot- Savart law. Use to obtain the magnetic field at a point due to a long, staright current carrying wire.

Text Solution

Verified by Experts

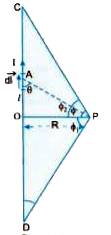
For statement of Biot - Savart law, refer to point Number 6 under the heading "Chapter At A Glance". Let CD be a long, staright current carrying wire and P be a point situated at a normal distance R from the wire. Consider a current element $I \to d l$ situated at a distance OA = I. If AP = r, then due to
$d B = \frac{μ_{0}}{4 π} \frac{I d l sin θ}{r^{2}}$
As per figure $sin θ = sin (90^{\circ} - ϕ) = cos θ$
$∴ I = R tan ϕ$
$∴ d l = R {sec}^{2} ϕ \cdot d ϕ$
and $r = R sec ϕ$
$∴ d B = \frac{μ_{0}}{4 π} \cdot \frac{(R {sec}^{2} ϕ_{2} . d ϕ) cos ϕ}{(R {sec ϕ}^{2})} = \frac{μ_{0}}{4 π} \cdot \frac{I cos ϕ \cdot d ϕ}{R}$
Therefore, the magnetic field due to whole wire CD will be
$B = \frac{μ_{0} I}{4 π R} \int_{- ϕ_{1}}^{ϕ_{2}} cos ϕ . d ϕ = \frac{μ_{0} I}{4 π R} [{sin ϕ}_{2} - sin (- ϕ_{1})] = \frac{μ_{0} I}{4 π R} [{sin ϕ}_{2} + {sin ϕ}_{2}]$
Here $ϕ_{2}$ has been taken +ve but $ϕ_{1}$ has been taken -ve because it is in a direction opposite to that of $ϕ_{2}$
For a long long wire (or infinitely long wire) $ϕ_{1} = ϕ_{2} = 90^{\circ}$ , therefore
$B = \frac{μ_{0} I}{2 π R}$

|

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

The direction of magnetic field at a point due to an infinitely long wire carrying current is
Aparallel to the current
Bantiparallel to the current
Calong the perpendicular drawn from a point on the wire
Dperpendicular to the plane containing the conductor and the point

U-LIKE SERIES-MOVING CHARGES AND MAGNETISM -LONG ANSWER QUESTIONS-I

Home
Ask Doubt
Profile