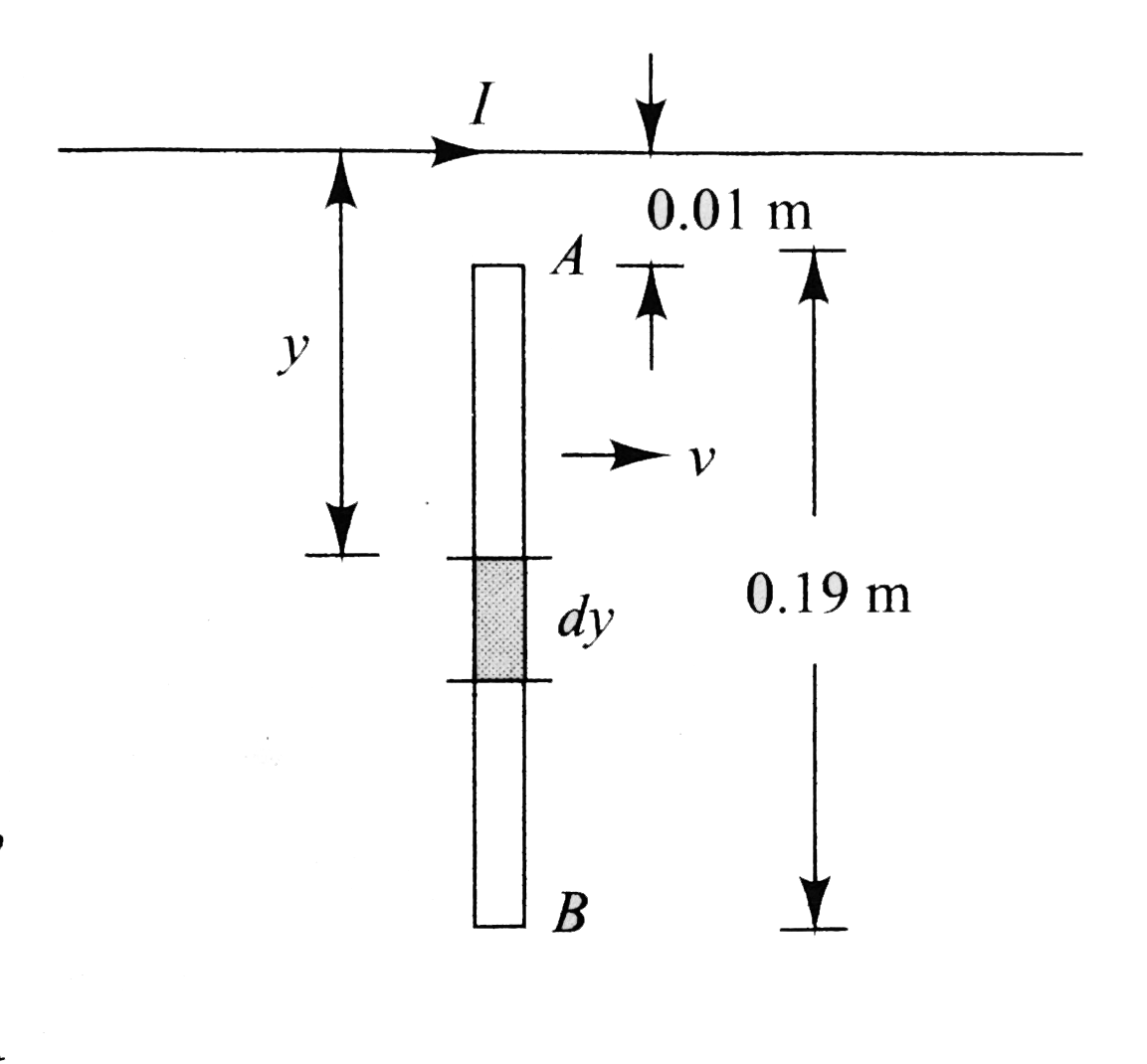
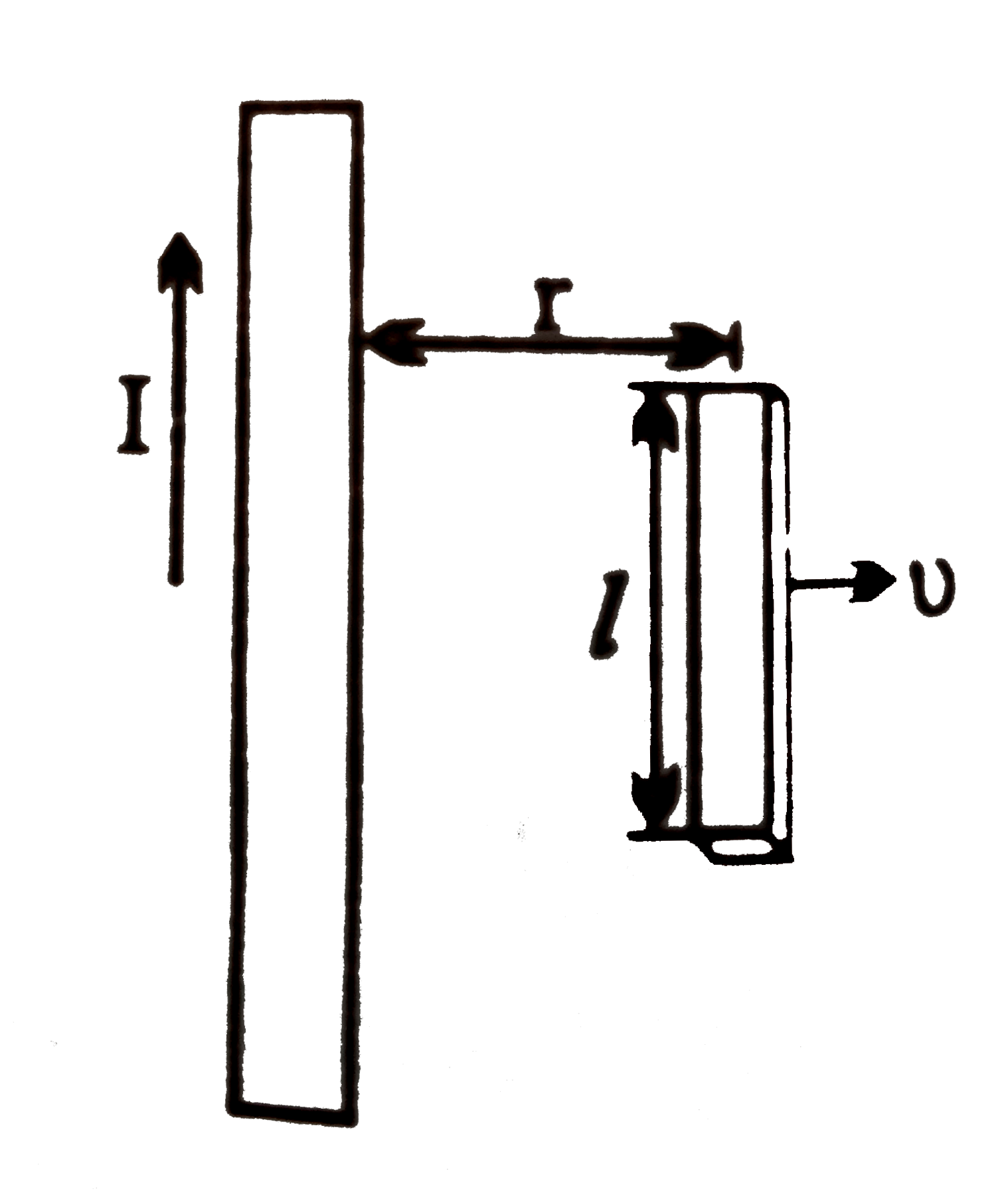
A copper rod of length 0.19m is moving with uniform velocity 10ms−1 parallel to a long straight wire carrying a current of 5.0A. The rod is perpendicular to the wire with its ends at distances 0.01 and 0.2m from it. Calculate the emf induced in the rod.
As shown in Fig.3.55, consider an element of length dy at a distance y from the wire, then at this position of the element, the magnetic field due to the current - carrying wirePQ will be B=μ04π2Iy into the plane of the paper.
So, the emf induced in the element dε=Bvdy=μ04π2Iyvdy and hence the emf induced across the ends of the rod due to its motion in the field of the wire,
ε=∫badε=μ04π2Iv∫badyy, i.e., ε=μ04π2Ivloge(ba)
Substituting the given data with b=(a+l),
ε=10−7×2×5×10loge=0.200.01=10−5×loge20
=30μV
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Solved Example
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 3.1
15 Videos
- ELECTROMAGENTIC INDUCTIONBOOK - CENGAGE PHYSICSCHAPTER - ELECTROMAGENTIC INDUCTIONEXERCISE - QUESTION BANK
40 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICSCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
A copper rod of length L is moving at a uniform speed v parallel to along straight wire carrying a current of I as shown in figure-5.25. The rod is perpendicular to the wire with its ends at distance a and b from if . Calculate the motional EMF induced in the rod.
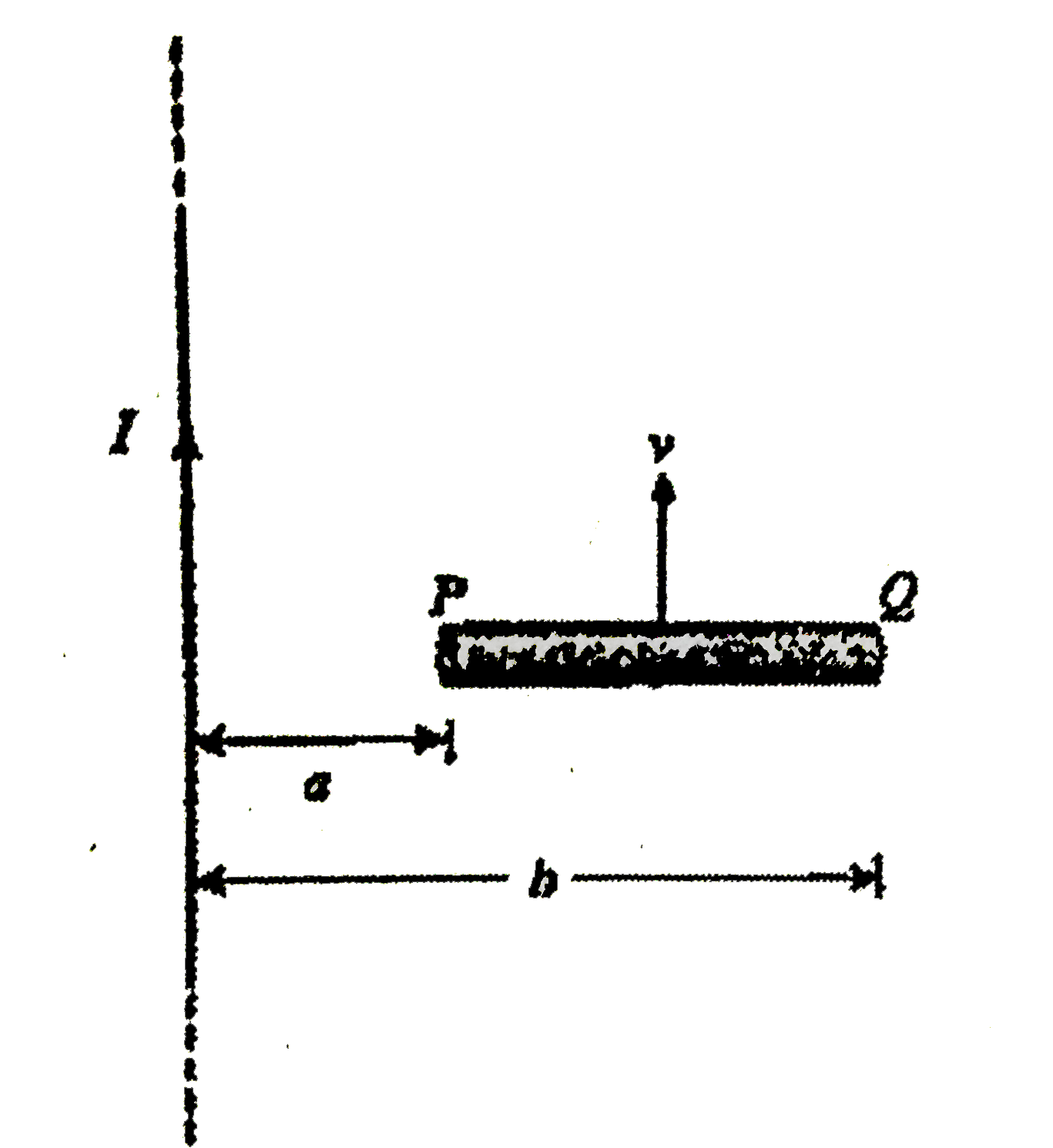
View SolutionA conducting rod length 1m moves with a speed of 2m/s parallel to a straight long wire carrying 4A current. Axis of rod is kept perpendicular to the wire with its near end at a distance of 1m from the wire. Magnitude of induced emf in rod is N×10−7log16volt. Find the value of N.
View Solution
Knowledge Check
A uniform metal rod is moving with a uniform velocity v parallel to a long straight wire carrying a current I. The rod is perpendicular to the wire with its ends at distance r1andr2 (with r2>r1) form it. The E.M.F. induced in the rod at that instant is
AzeroBμ0Iv2πln(r2r1)Cμ0Iv2πln(r1r2)Dμ0Iv4π(1−r1r2)A copper rod moves with a constant angular velocity ω about a long straight wire carrying a current I. If the ends of the rod from the wire are at distances a and b, then the e.m.f induced in the rod is
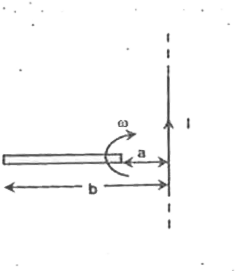 Aμ0i(wa)2πIn(ba)Bμ0i(wb)2πIn(ba)CzeroDμ0iw(a+b)4πIn(ba)
Aμ0i(wa)2πIn(ba)Bμ0i(wb)2πIn(ba)CzeroDμ0iw(a+b)4πIn(ba)Shows a copper rod moving with velocity v parallel to a long straight wire carrying current =100A. Calculate the induced emf in the rod, where v=5mS−1, a=1cm , b=100cm.
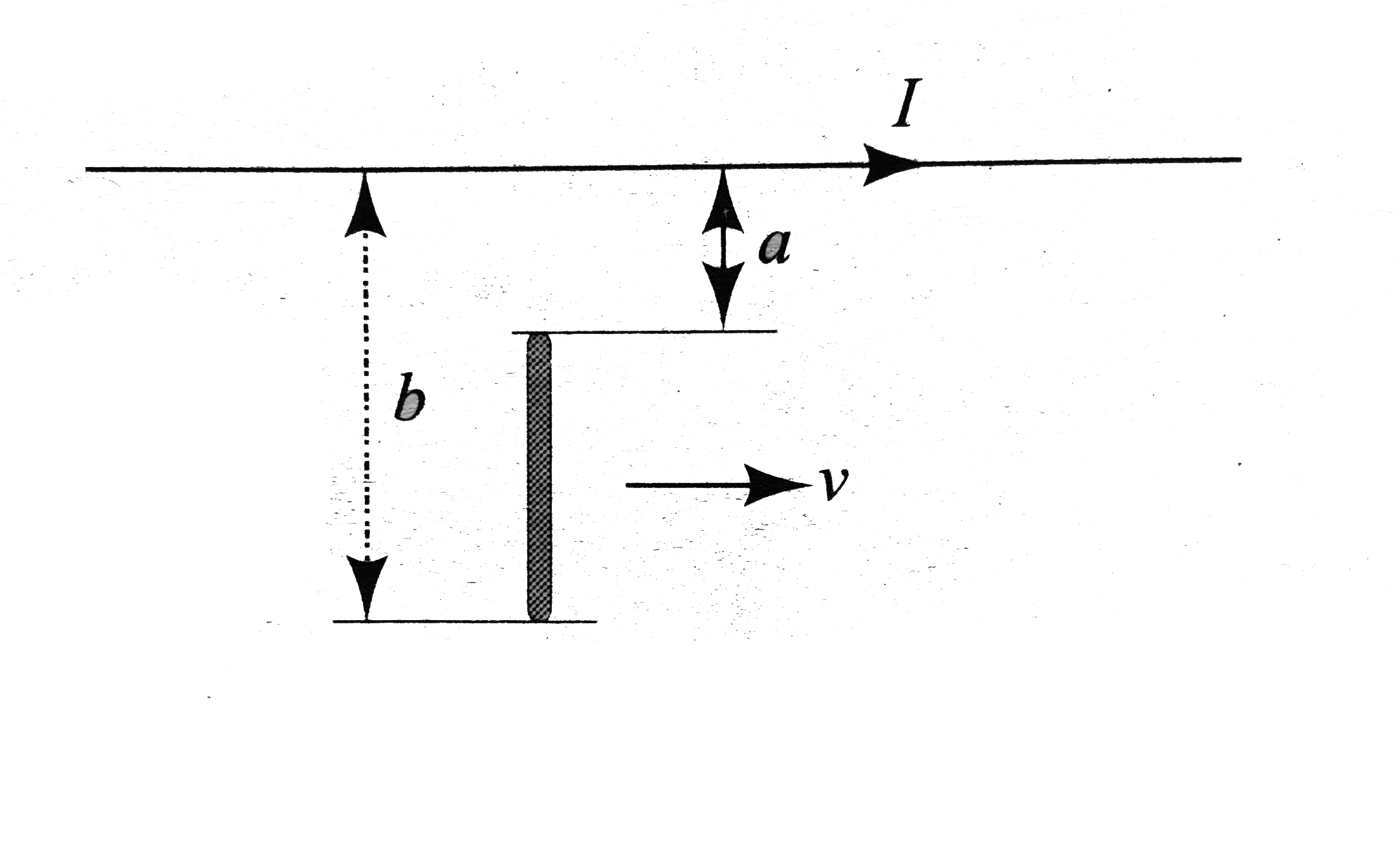 A(a) 0.23mVB(b) 0.46mVC( c) 0.16mVD(d) 0.32mV
A(a) 0.23mVB(b) 0.46mVC( c) 0.16mVD(d) 0.32mV
A rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance a from the wire.

View SolutionA rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance ‘a’ from the wire.
View SolutionA glass rod of length l moves with velocity in a uniform magnetic field B. What is the e.m.f. induced in the rod ?
View SolutionA cionducing rod moves with constant velocity v perpendicular to the straight wire carrying a current I as shown compute that the emf generated between the ends of the rod
View SolutionA metal rod of length 2 m is rotating with an angualr velocity of 100rads−1 in plane perpendicular to a uniform magnetic field of 0.3 T. The potential difference between the ends of the rod is
View Solution
