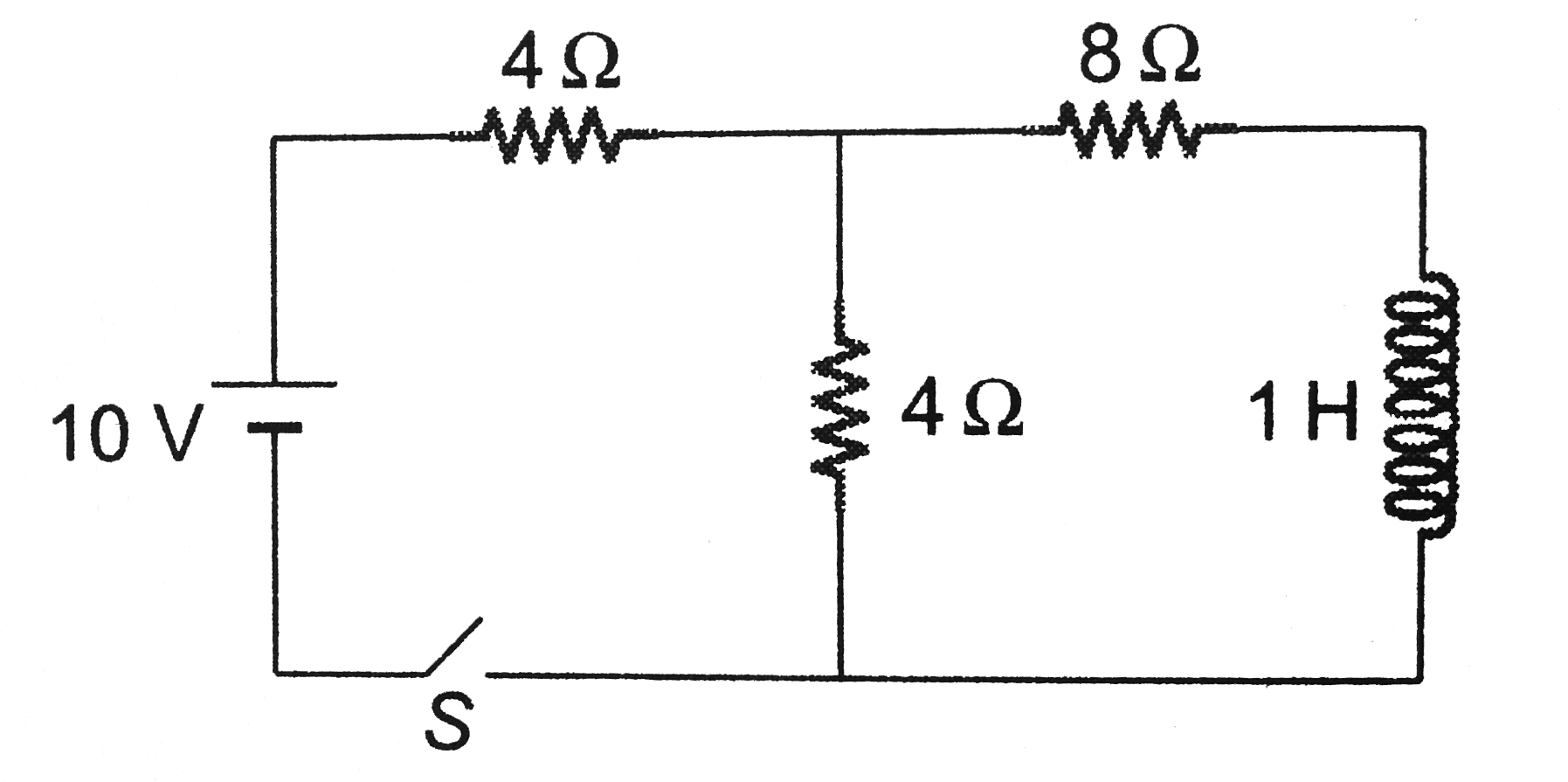
In the following circuit (Fig.)the switch is closed at t=0. Intially, there is no current in inductor. Find out the equation of current in the inductor coil as s function of time.
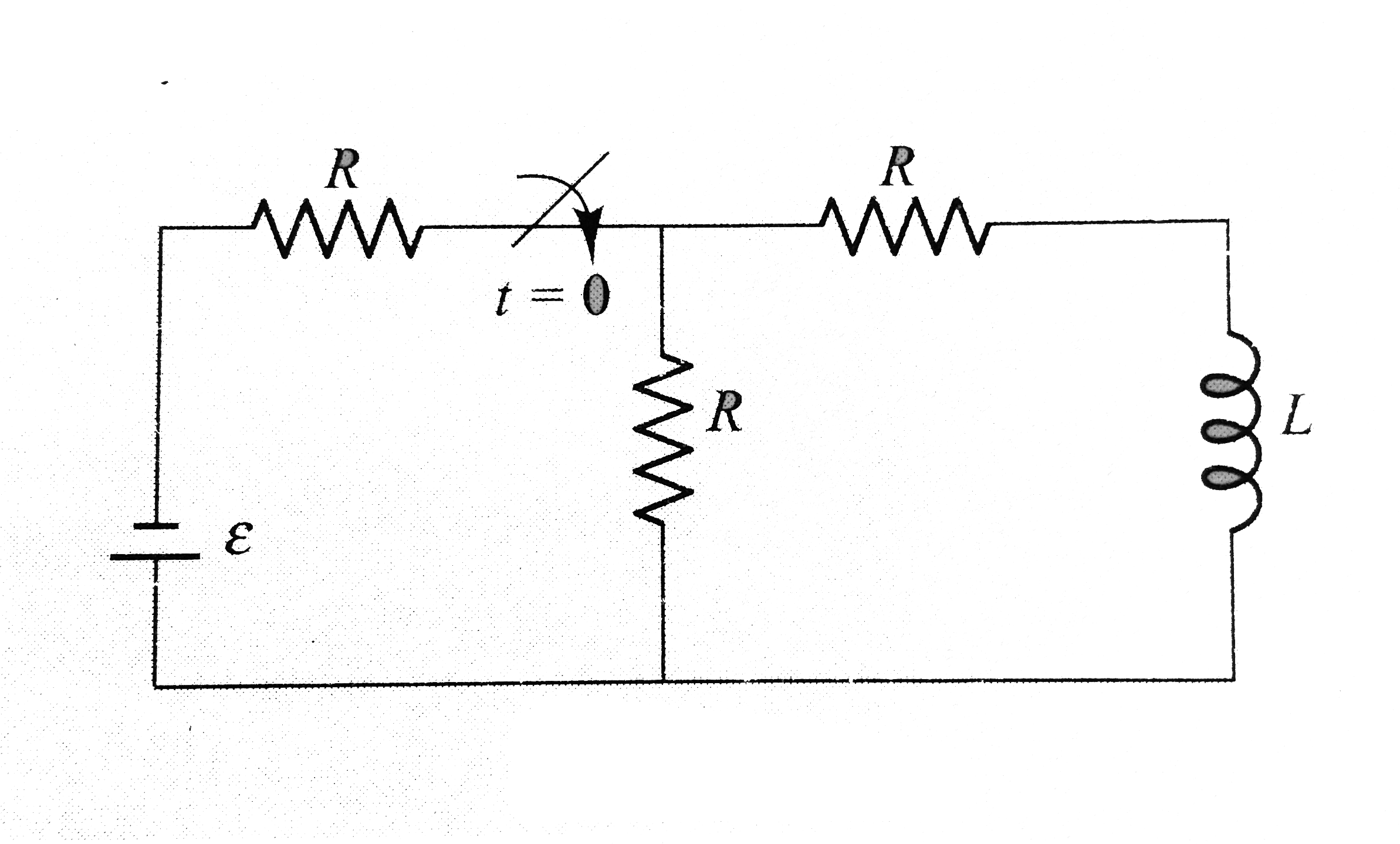
At any time t,−ε+i1R−(i−i1)R=0
−ε+2i1R−iR=0
i1=iR+ε2R
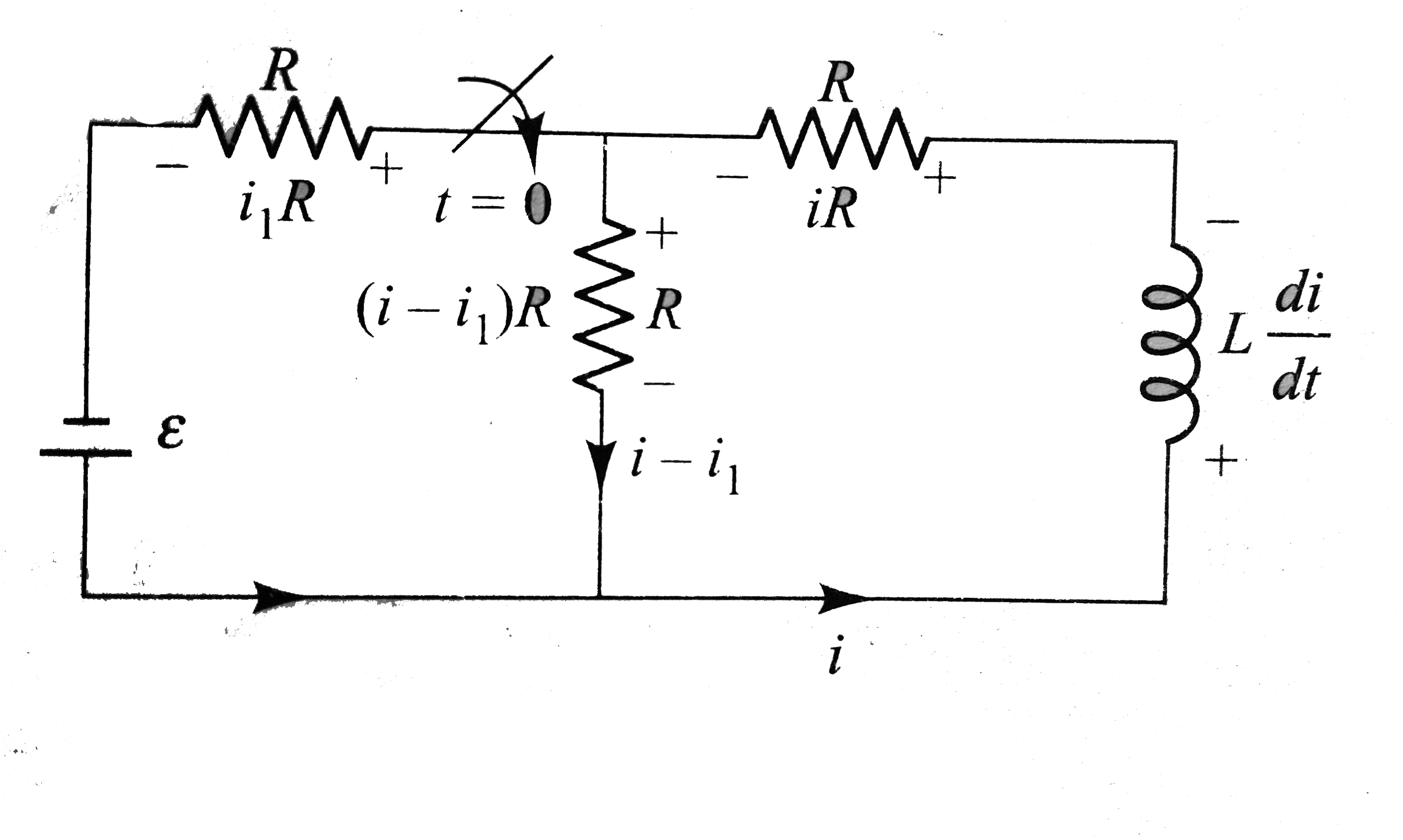
Now
−ε+i1R+iR+Ldidt=0
−ε+(iR+ε2)+iR+Ldidt=0
ε2+3iR2=−Ldidt
(ε+3iR2)dt=−Ldi⇒−∫t0dt2L=∫i0di−ε+3iR
t2L=13R In (−ɛ+3iR−ɛ)⇒−In(−ɛ+3iR−ɛ)=3Rt2L
i=+ɛ3R(1−e−3Rt2L)
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Solved Examples
3 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Exercise 4.1
24 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
28 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
Similar Questions
In the following circuit the switch is closed at t=0.Intially there is no current in inductor.Find out current the inductor coil as a function of time.
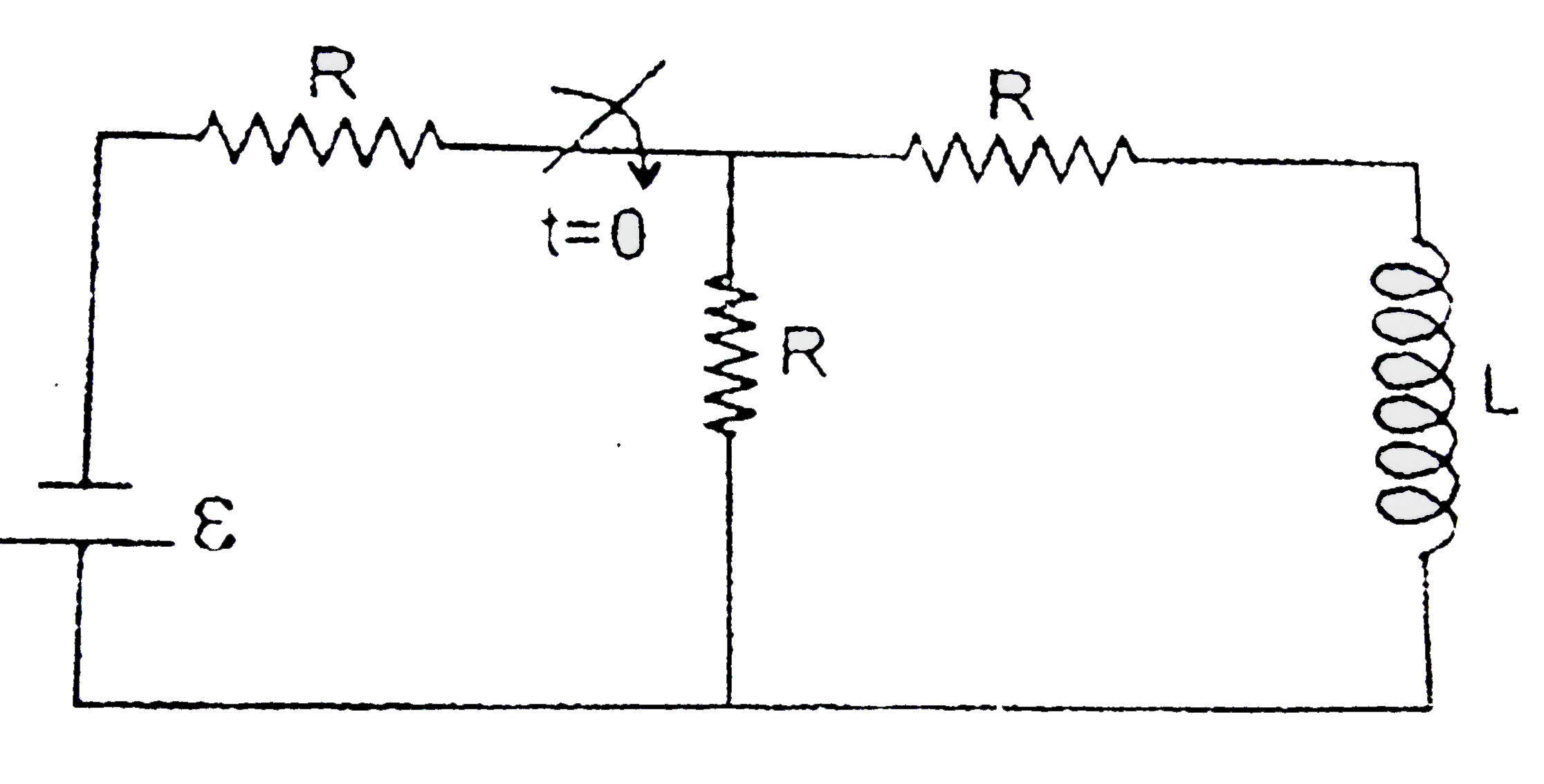
View SolutionIn the following circuit the switch is closed at t=0.Intially there is no current in inductor.Find out current the inductor coil as a function of time.
View Solution
Knowledge Check
In adjacent circuit, switch S is closed at t = 0. The time at which current in the circuit becomes half of the steady current is
 Aτln2Bln2τC2τln2Dτ2ln2
Aτln2Bln2τC2τln2Dτ2ln2
The switch in figure is closed at time t=0. Find the current in the inductor and the current through the switch as functions of time thereafter.
View SolutionThe switch in figure is closed at time t=0. Find the current in the inductor and the current through the switch as functions of time thereafter.

View SolutionFigure shows a circuit consisting of an ideal cell, an inductor L, and a resistor R, connected in series. Let switch S be closed at t=0. Suppose at t=0, the current in the inductor is io, then find out the equation of current as a function of time.

View SolutionFigure shows a circuit consisting of an ideal cell, an inductor L, and a resistor R, connected in series. Let switch S be closed at t=0. Suppose at t=0, the current in the inductor is io, then find out the equation of current as a function of time.

View SolutionFigure shows a circuit consisting of an ideal cell, an inductor L, and a resistor R, connected in series. Let switch S be closed at t=0. Suppose at t=0, the current in the inductor is io, then find out the equation of current as a function of time.

View SolutionIn the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.

View SolutionIn the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.

View Solution
