Figure shows a circuit consisting of an ideal cell, an inductor L, and a resistor R, connected in series. Let switch S be closed at t=0. Suppose at t=0, the current in the inductor is io, then find out the equation of current as a function of time.

Let an instant t current in the circuit is i which is increasing at the rate di/dt
Writing KVL along the circuit, we have ε−Ldidt−iR=0
⇒Ldidt=ε−iR⇒i∫i0diε−iR=t∫0dtL
⇒ln(ε−iRε−i0R)=−RtL
⇒ε−iR=(ε−i0R)e−Rt/L⇒i=ε−i(ε−i0R)eRt/LR
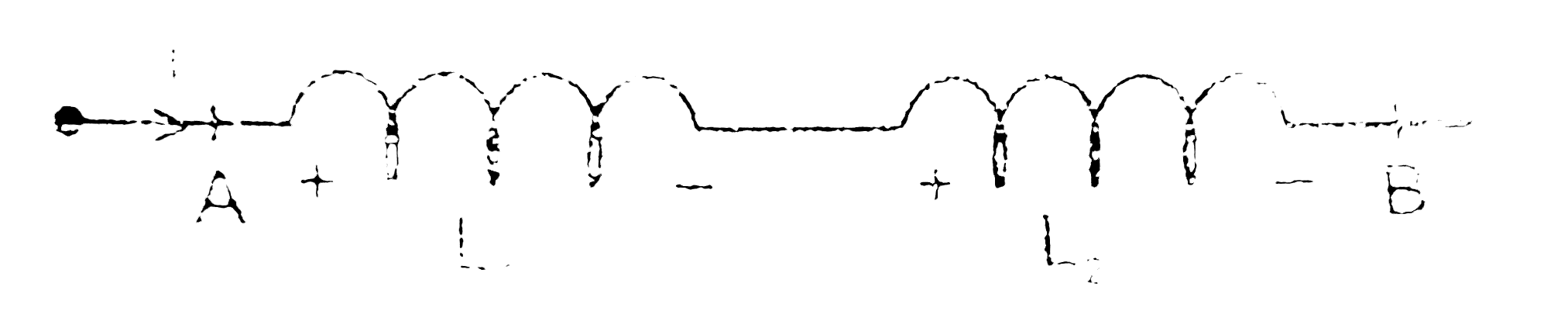
Equivalent self inductance:
Series combination:
from (1) and (2) L=L1+L2(neglecting mutual inductance)
Parallel Combination:
From figure VA−VB=L1dt1dt=L2dt2dt ...(3)
also i=i1+i2
or didt=di1dt+di2dt
or VA−VBL=VA−VBL1+VA−VBL2 (neglecting mutual inductance)
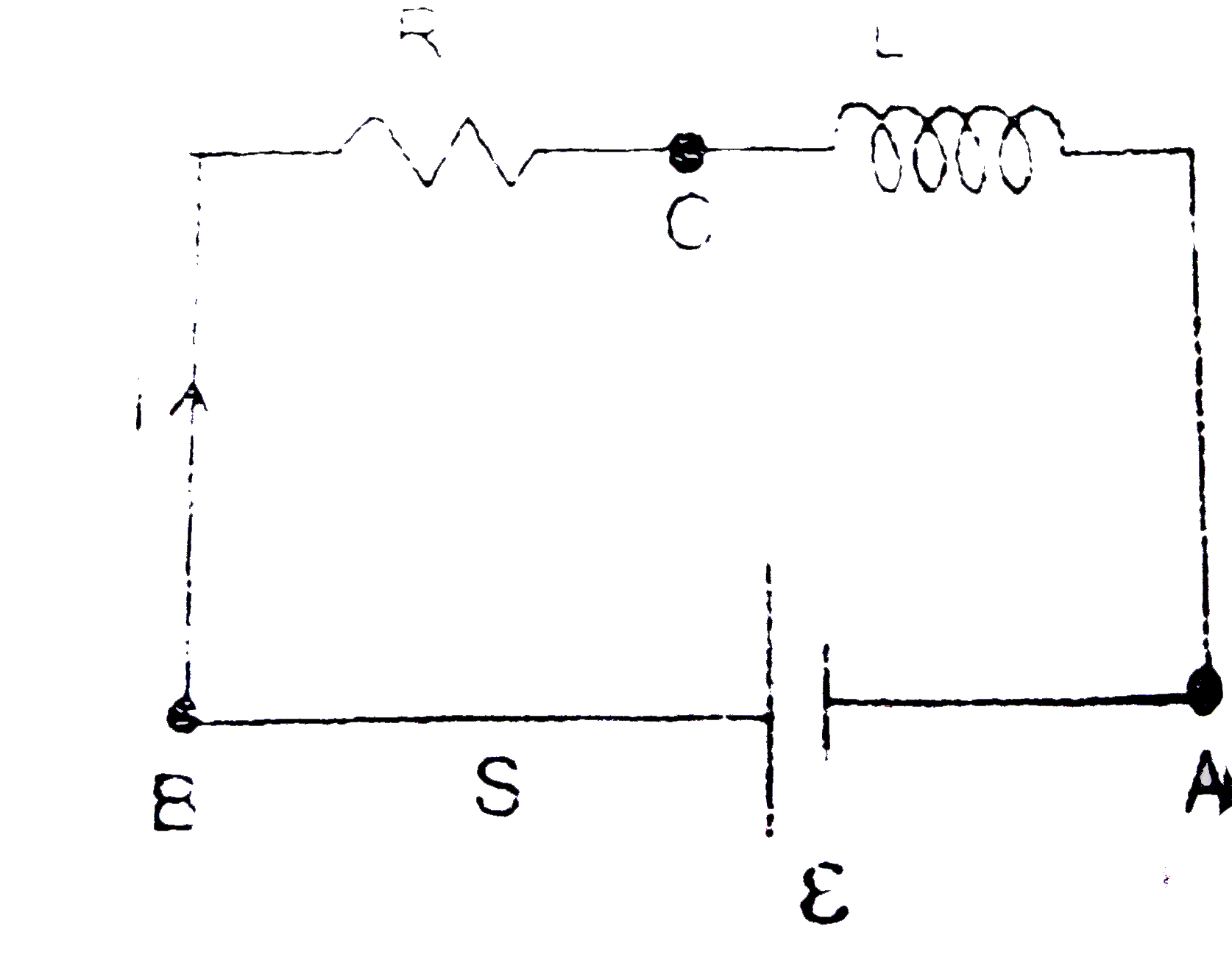
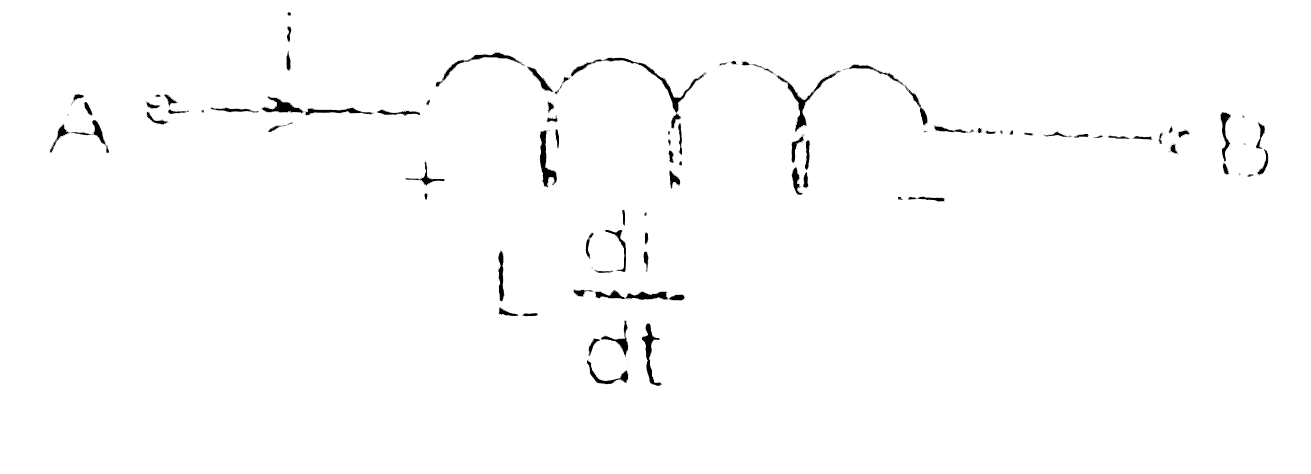
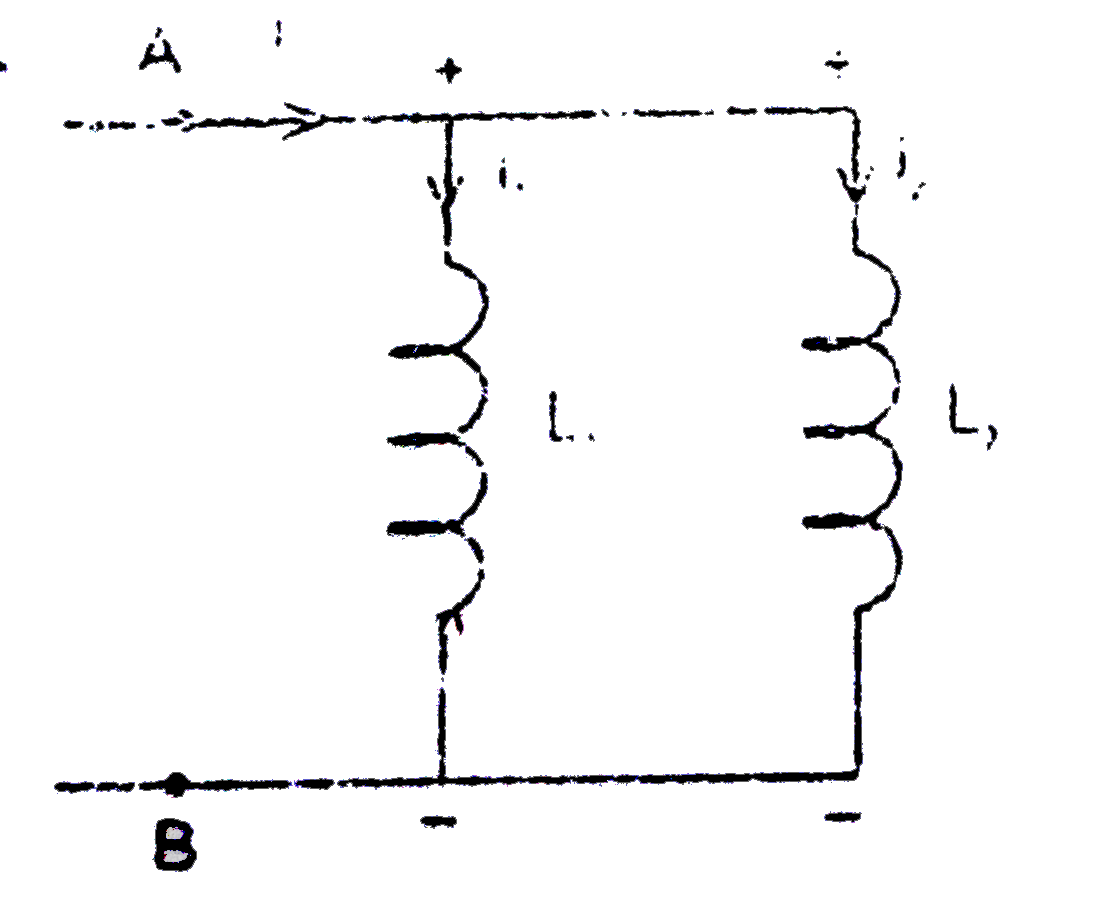
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Problem12videos
ELECTROMAGNETIC INDUCTION
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-163videos
ELECTROMAGNETIC INDUCTION
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems31videos
ELECTRODYNAMICS
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP40videos
ELECTROSTATICS
Similar Questions
Two inductors are connected in parallel and switch S is closed at t=0
 View Solution
View SolutionIn the following circuit (Fig.)the switch is closed at t=0. Intially, there is no current in inductor. Find out the equation of current in the inductor coil as s function of time.
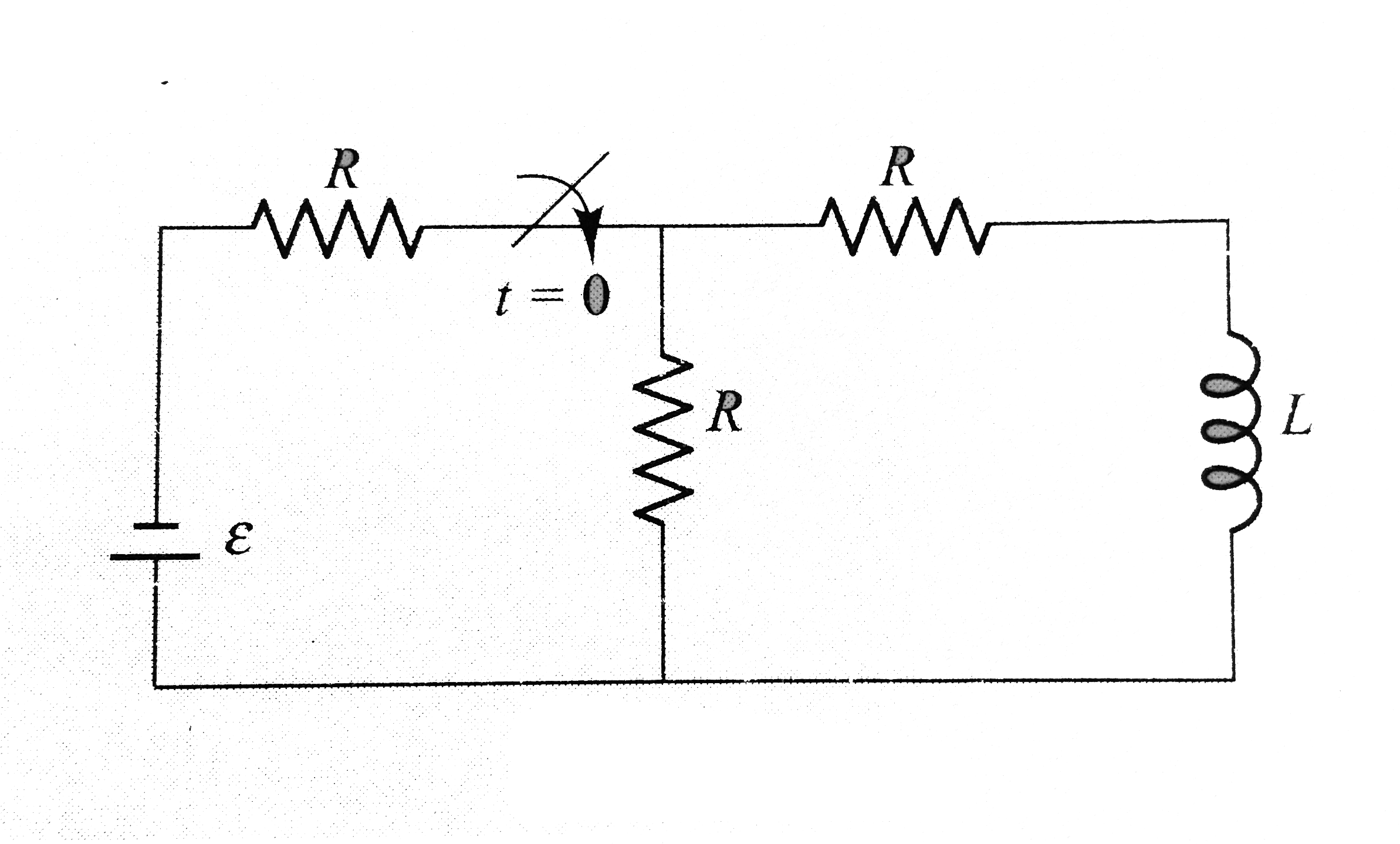 View Solution
View SolutionFigure below shows a capacitor C, an inductor L and a resistor R, connected in series to an a.c. supply of 220 V.
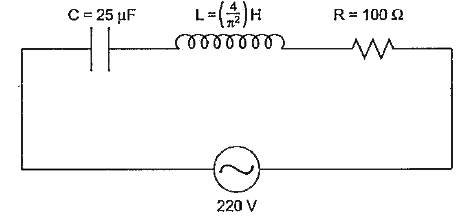
Average power consumed by the circuit.View SolutionIn the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.
 View Solution
View SolutionThe switch in figure is closed at time t=0. Find the current in the inductor and the current through the switch as functions of time thereafter.
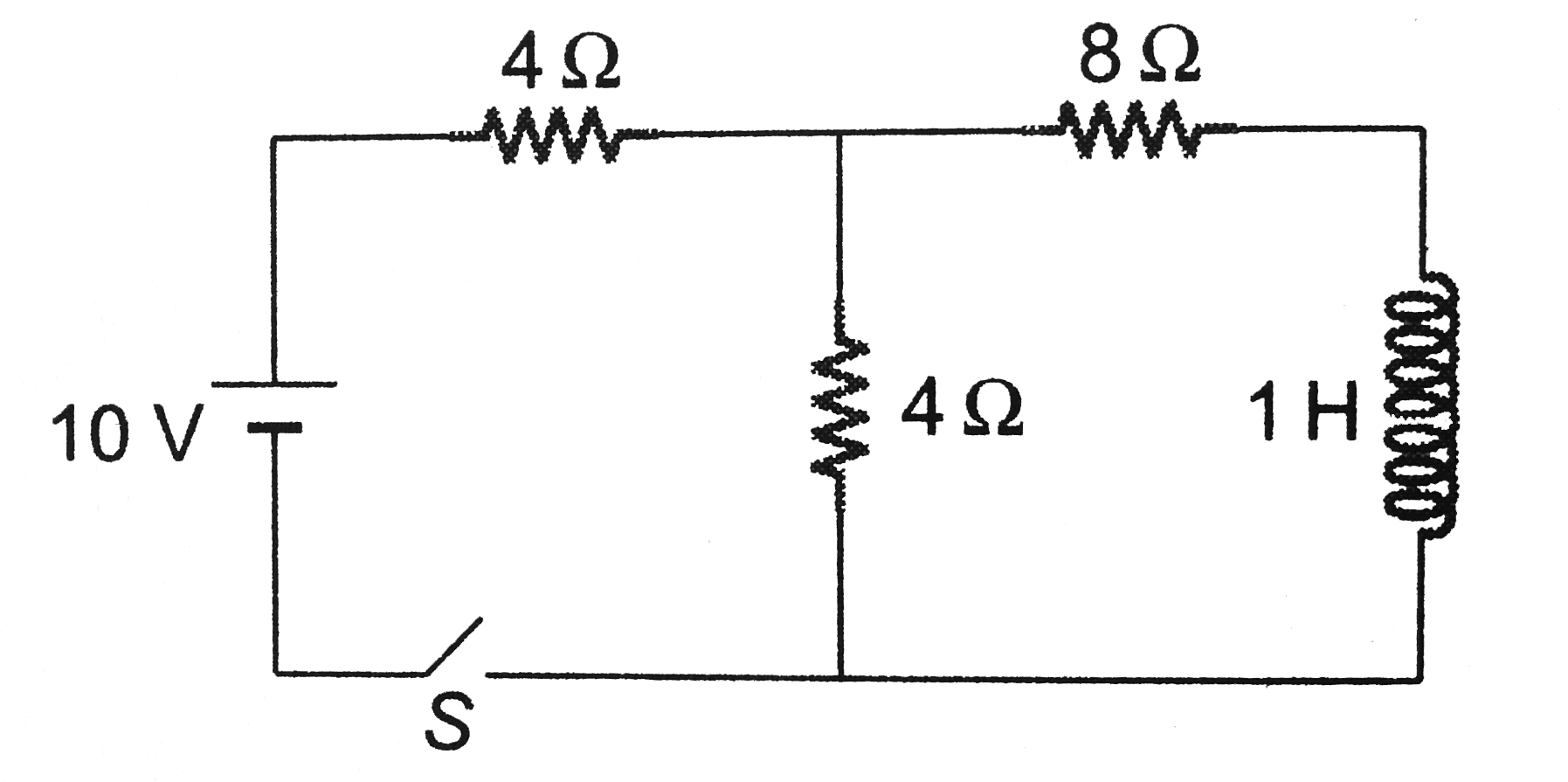 View Solution
View SolutionSwitch is closed at t=0 then the current in the circuit at t=L2R is
_PHY_E06_157_Q01.png) View Solution
View SolutionFigure below shows a capacitor C, an inductor L and a resistor R, connected in series to an a.c. supply of 220 V.
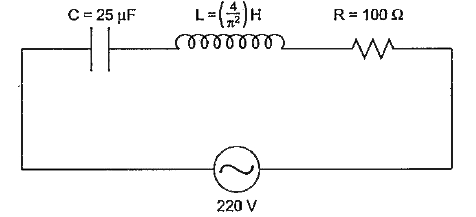
Current flowing through the circuit.View SolutionA circuit contains an ideal cell and an inductor with a switch. Initially, the switch is open. It is closed at t=0. Find the current as a function of time.
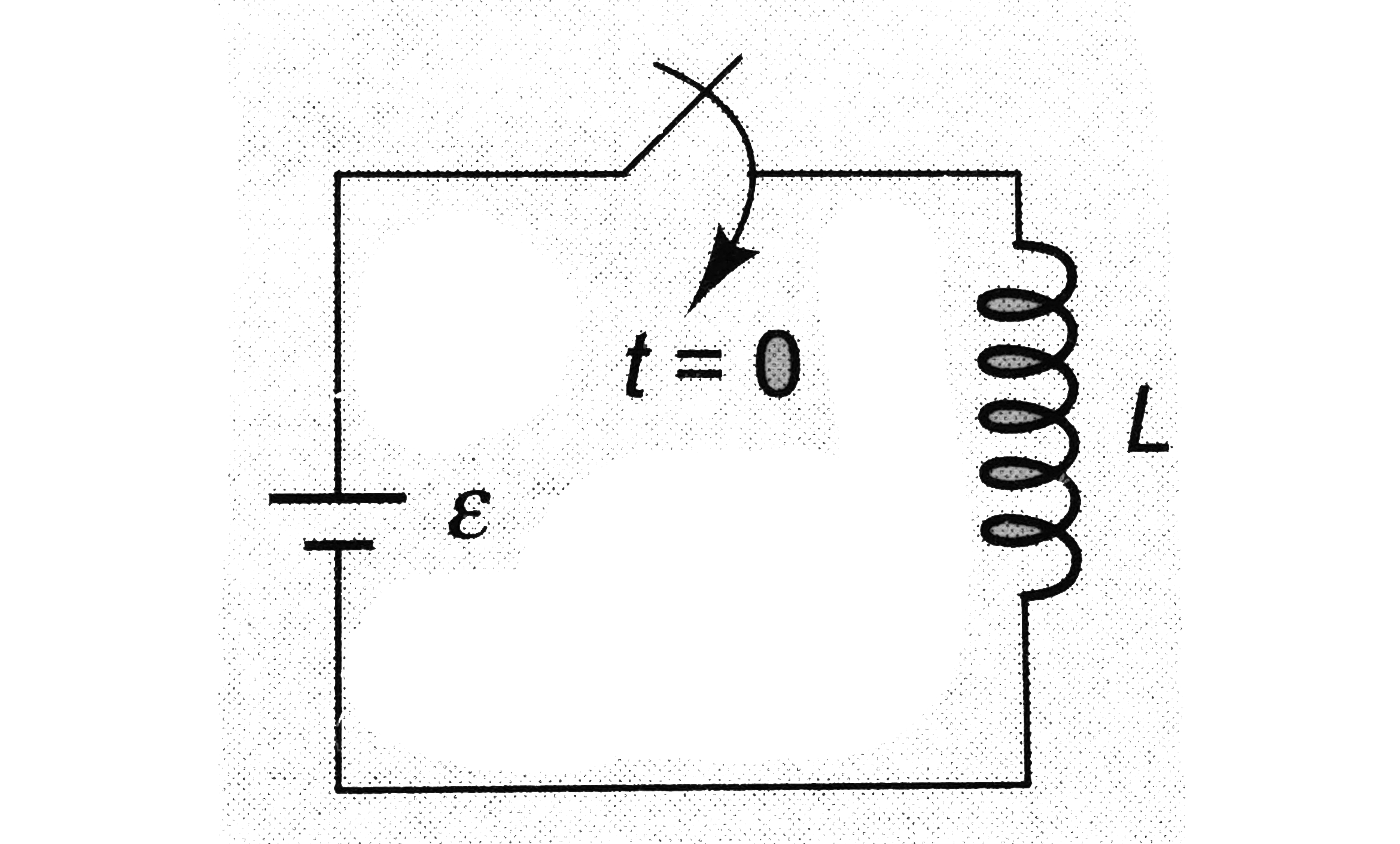 View Solution
View SolutionA circuit contains an ideal cell and an inductor with a switch. Initially, the switch is open. It is closed at t=0. Find the current as a function of time.
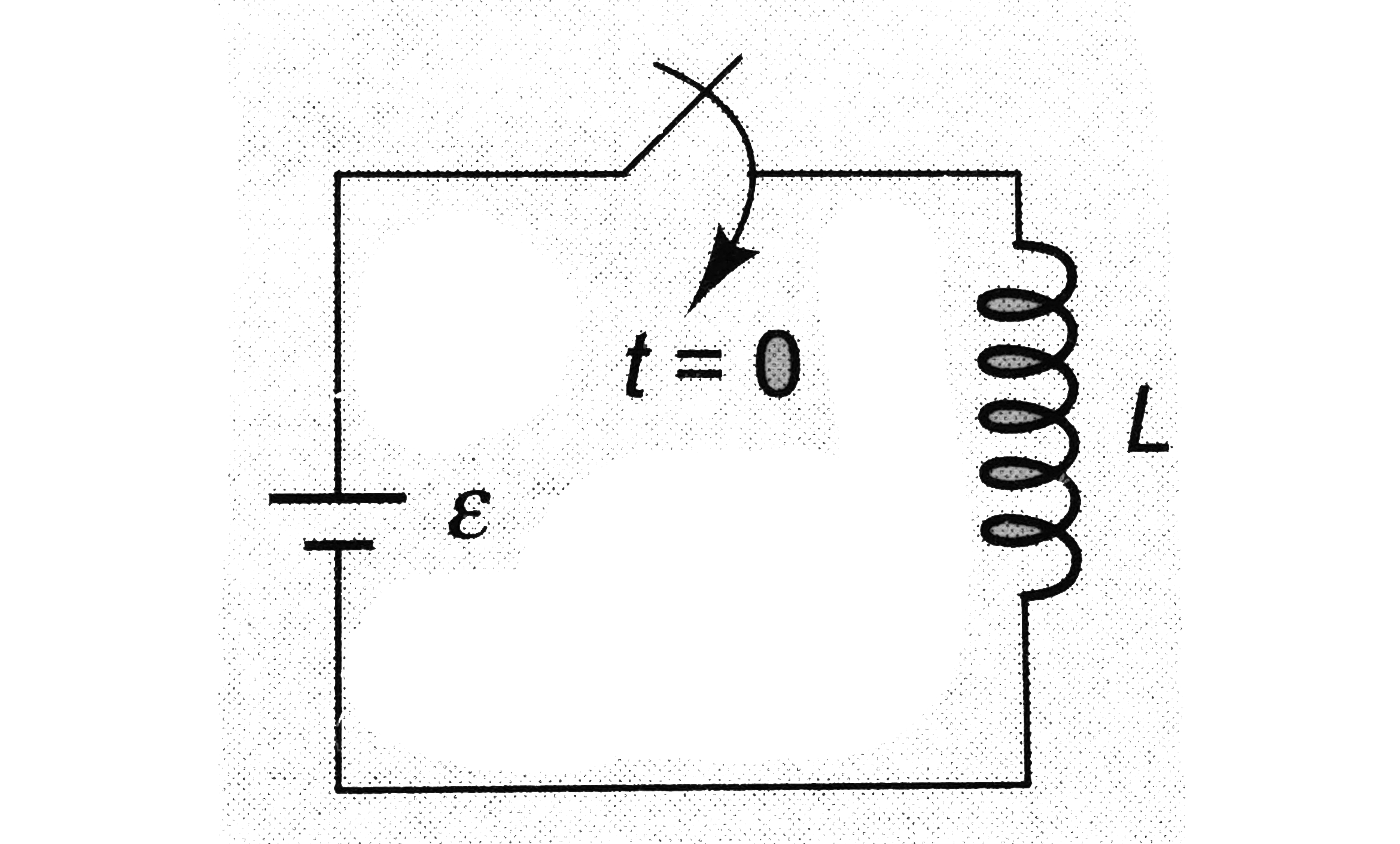 View Solution
View SolutionIn the circuit shown in figure L=10H,R=5Ω,E=15V. The switch S is closed at t=0. At t=2s the current in the circuit is
 View Solution
View Solution

