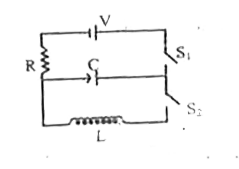
In the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).
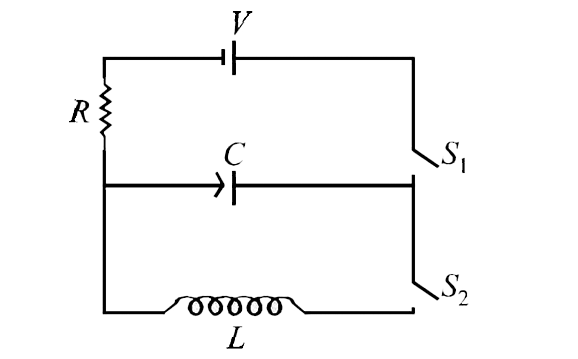
When the capacitor gets charged compleely, (=(S1) is opened and (S2) is closed, Then,
at t=0, energy stored in the circuit is purely in the from of magnetic energy.
at any time t>0 current in the circuit is in the same direction.
at t>0, there is no excharge of energy between the inductor and capacitor.
at any time t>0, maximum instantaneous current in the circuit may be V√CL⋅
The correct Answer is:D
From conservation of energy,
12LI2max=12CV2⇒ImaxV√CL
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Archives (integer)2videos
INDUCTANCE
- BOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Subective Type2videos
INDUCTANCE
- BOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Archives (multiple Correct)3videos
INDUCTANCE
- BOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit28videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank31videos
KINETIC THEORY
Similar Questions
The capacitor of capacitance C can be charged (with the help of a resistance R) by a voltage source V, by closing switch S1 while keeping switch S2 open.The capacitor can be connected in series with an series with an inductor L by closing switch S2 and opening S1.
Initially the capacitor was uncharged.Now switch S1 is closed and S2 is kept open.If time constant of this circuit is t, then
 View Solution
View SolutionThe capacitor for capacitance C can be charged ( with the help of a resistance R) by a voltage source V, by closing switch S1 while keeping switch S2 open. The capacitor can be connected in series with an inductor 'L' by closing switch S2 and opening S1.

After the capacitor gets fully charged S1 is opened and S2 is closed so that the inductor is connected in series with the capacitor. Then,View Solution
Knowledge Check
- Question 1 - Select One
In the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).
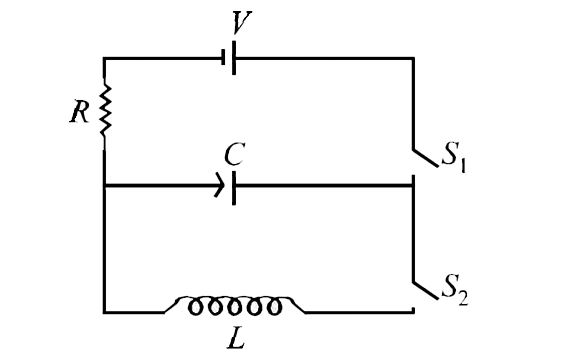
At the start, the capicitor was uncharged. when switch (S1) is closed and (S2) is kept open, the time constant of this circuit is τ. which of the following is correctAafter interval τ charge on the capcitor is CV2Bafter interval 2τ charge on the capcitor is (CV)(1−e−2)Cthe work done by the voltage source will be half of the heat dissipated when the capacitor is fully chargedDafter time interval 2τ, charge on the capacitor is CV(1−e−1 - Question 2 - Select One
In the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).
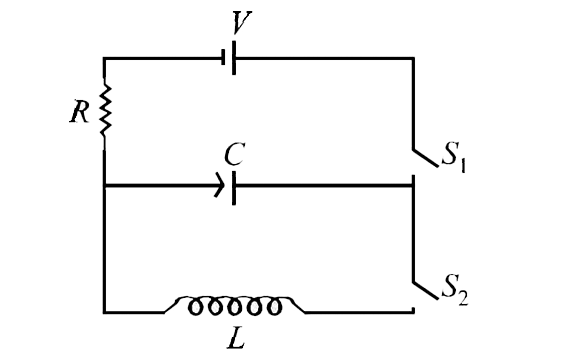
Given taht the total charge stored in the LC circuit is (Q0). for Tge0, the charge on the capacitor isAQ=Q0cos(π2+t√LC)BQ=Q0cos(π2−t√LC)CQ=−LCd2Qdt2DQ=−1√LCd2Qdt2 - Question 3 - Select One
The capacitor of capacitance C can be charged (with the help of a resistance R) by a voltage source V, by closing switch S1 while keeping switch S2 open. The capacitor can be connected in series with an inductor ‘L’ by closing switch S2 and opening S1

After the capacitor gets fully charged, S1 is opened and S2 is closed so that the inductor is connected in series with the capacitor. Then,Aat t = 0, energy stored in the circuit is purely in the form of magnetic energyBat any time t > 0, current in the circuit is in the same direction.Cat t > 0, there is no exchange of energy between the inductor and capacitorDat any time t > 0, instantaneous current in the circuit may V√CL
After the capacitor gets fully charged, S1 is opened and S2 is closed so that the inductor is connected in series with the capacitor. Then,
View SolutionThe capacitor of capacitance C can be charged (with the help of a resistance R) by a voltage source V, by closing switch S1 while keeping switch S2 open.The capacitor can be connected in series with an series with an inductor L by closing switch S2 and opening S1.
After the capacitor gets fully charged S1 is opened and S2 is closed so that the inductor is connected in series with the capacitor.Then
 View Solution
View SolutionThe capacitor of capacitance C can be charged (with the help of a resistance R ) by a voltage source V, by closing switch S1 while keeping switch S2 open. The capacitor can be connected in series with an inductor 'L' by closing switch S2 and opening S1.

Initially, the capacitor was uncharged. Now , switch S1 is closed and S2 is kept open. if time constant of this circuit is τ, thenView SolutionIn the circuit shown, the capacitor initially charged with a 12V batteryy, when switch S1 is open and switch S2 is closed. The maximum value of current in the circuit when S2 is opened and S2 is closed is
 View Solution
View SolutionThe capacitor of capacitance C can be charged (with the help of a resistance R ) by a voltage source V, by closing switch S1 while keeping switch S2 open. The capacitor can be connected in series with an inductor 'L' by closing switch S2 and opening S1.
If the total charge storge in the LC circuit is Q0, then for t ≥ 0View Solution

