After the capacitor gets fully charged, S1 is opened and S2 is closed so that the inductor is connected in series with the capacitor. Then,
at t=0,energy stored in the circuit is purely in the formed of magnetic energy.
at any time t>0, current in the circuit is in the same direction
at t>0, there is no exchange of energy between the inductor and capacitor
at any timet>0instantaneous current in the circuit mayV√CL
The correct Answer is:D
Q=Q0cosωt=CVcosωt
I=dQdt=−ωCVsinωt
Imax=ωCV=1LCC.V=V√CL
I=−V√CLsinωt
Similar Questions
In the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).
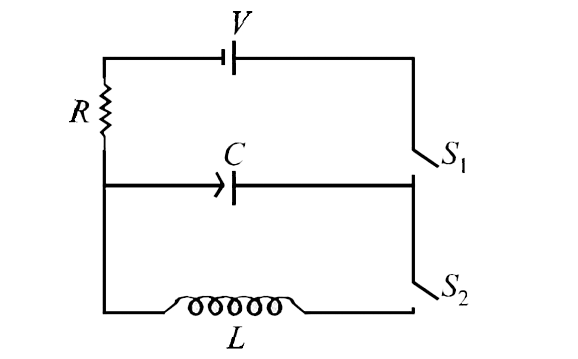
When the capacitor gets charged compleely, (=(S1) is opened and (S2) is closed, Then,
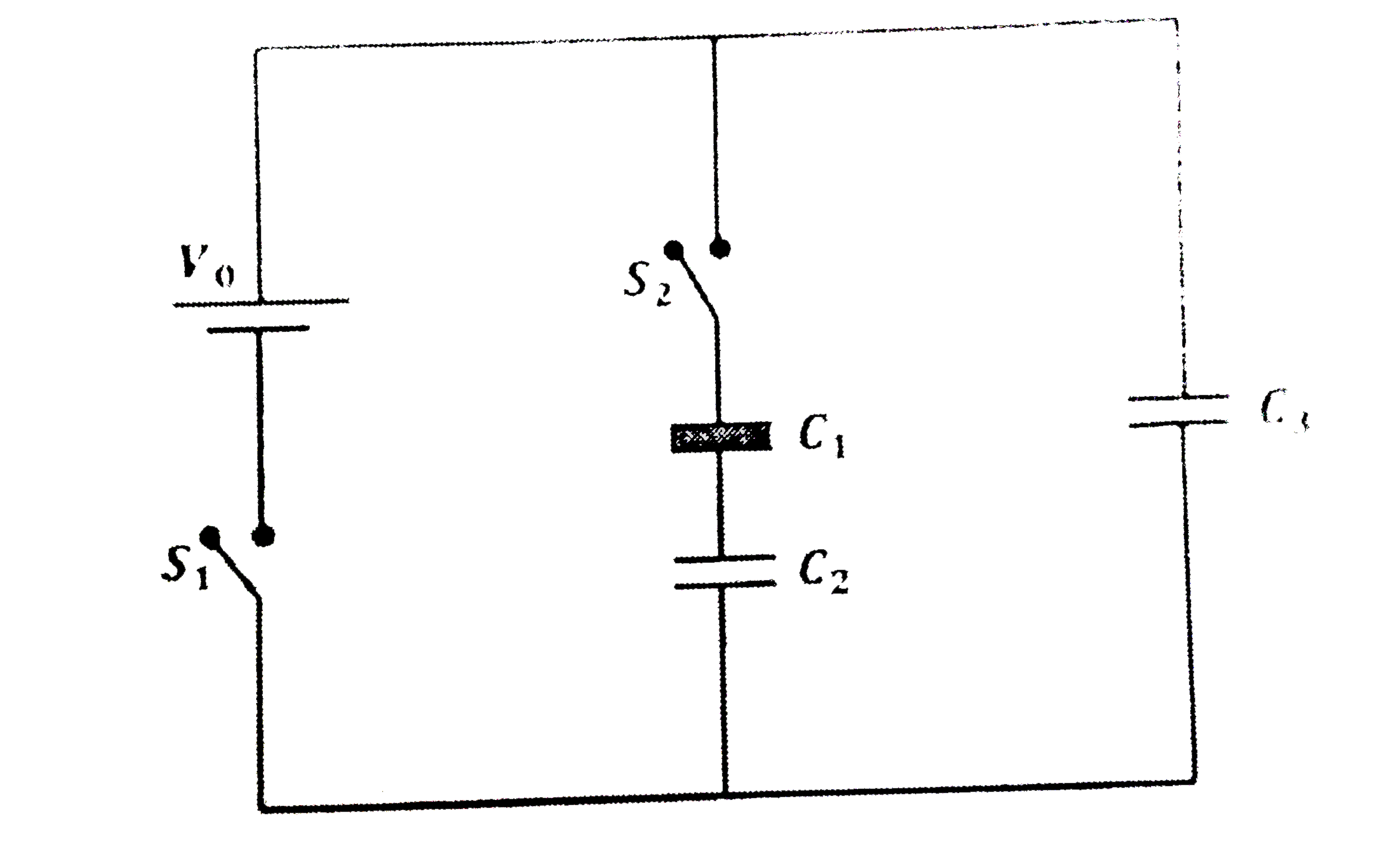
View SolutionThree identical capacitors C1,C2 and C3 have a capacitance of 1.0μF each and they are uncharged initially. They are connected in a circuit as shown in the figure and C1 is then filled completely with a dielectric material of relative permittivity εr. The cell electromotive force (emf) V0=8V. First the switch S1 is closed while the switch S2 is kept open. When the capacitor C3 is fully charged, S1 is opened and S2 is closed simultaneously. When all the capacitors reach equilibrium, the charge on C3 is found to be 5μc. The value of εr = ____________.
View Solution
Knowledge Check
In the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).

When the capacitor gets charged compleely, (=(S1) is opened and (S2) is closed, Then,Aat t=0 energy strored in the circuit is purely in the form of magnetic energyBat any time tgt0, current in the circuit is in the same directionCat tgt0, thre is no exchange of energy between the inductor and capacitorDat any time tgt0, instantaneous current in the circuit may be V√CVIn the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).
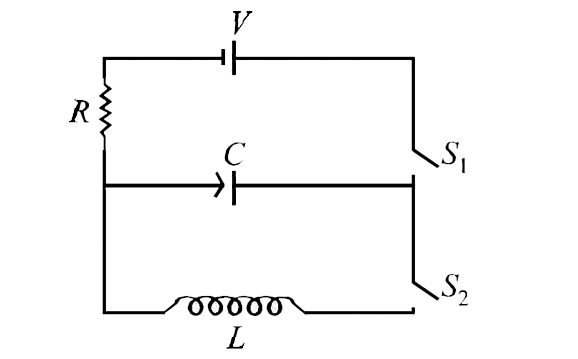
At the start, the capicitor was uncharged. when switch (S1) is closed and (S2) is kept open, the time constant of this circuit is τ. which of the following is correctAafter interval τ charge on the capcitor is CV2Bafter interval 2τ charge on the capcitor is (CV)(1−e−2)Cthe work done by the voltage source will be half of the heat dissipated when the capacitor is fully chargedDafter time interval 2τ, charge on the capacitor is CV(1−e−1In the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).
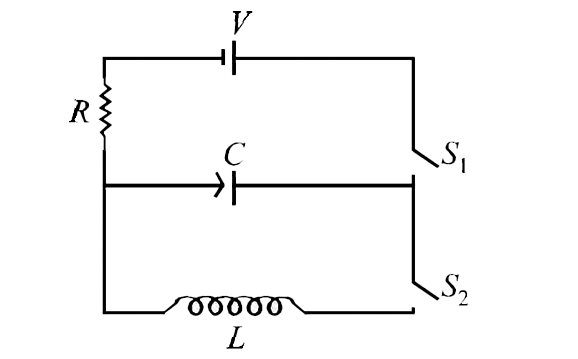
Given taht the total charge stored in the LC circuit is (Q0). for Tge0, the charge on the capacitor isAQ=Q0cos(π2+t√LC)BQ=Q0cos(π2−t√LC)CQ=−LCd2Qdt2DQ=−1√LCd2Qdt2
Three identical capacitors C1,C2 and C3 have a capacitance of 1.0μF each and they are uncharged initially. They are connected in a circuit as shown in the figure and C1 is then filled completely with a dielectric material of relative permittivity εr. The cell electromotive force (emf) V0=8V. First the switch S1 is closed while the switch S2 is kept open. When the capacitor C3 is fully charged, S1 is opened and S2 is closed simultaneously. When all the capacitors reach equilibrium, the charge on C3 is found to be 5μc. The value of εr = ____________.

View SolutionIn the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).

At the start, the capicitor was uncharged. when switch (S1) is closed and (S2) is kept open, the time constant of this circuit is τ. which of the following is correct
View SolutionIn the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).

Given taht the total charge stored in the LC circuit is (Q0). for T≥0 the charge on the capacitor is
View SolutionIn the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).

Given taht the total charge stored in the LC circuit is (Q0). for Tge0, the charge on the capacitor is
View SolutionIn the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).

Given taht the total charge stored in the LC circuit is (Q0). for Tge0, the charge on the capacitor is
View Solution
