A charged particle of specific charge s passes undeviated through region 1 as shown in Fig.

Velocity of paticle in rigion 1 is
Work done to move the charged particle in region 1 and region 2 is zero.
The radius of the trajectory of the charged particle in Region 2 is
The particle emerges from region 2 with a velocity vec(v') for
The correct Answer is:A, B, C, D
Net force on charge should be zero in region 1,
In region 1, net force is zero on particle, hence on work is done on particle in region 1,
In region 2, only magnetic force is there, hence no work is done in this region also.
In region 2:
If or, then particle will complete haf revolution in region 2 and come out of it with same velocity in opposite direction.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Linked Comprehension
84 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
- Moving charges and magnetismBOOK - CENGAGE PHYSICSCHAPTER - Moving charges and magnetismEXERCISE - Question Bank
20 Videos
Similar Questions
A charged particle of specific charge (Charge/mass) α is released from origin at time t=0 with a velocity given as
→v=v0(ˆi+ˆj)
The magnetic field in region is uniform with magnetic induction →B=B0ˆi. Coordinates of the particle at time t=πB0α are:
View SolutionA charge particle of charge q and mass m is moving with velocity v as shown in fig In a uniform magnetic field B along -ve z-direction.Select the correct alternative (s).

View Solution
Knowledge Check
A charged particle of specific charge s moves undeflected through a region of space containing mutually perpendicular and uniform electric and magnetic fields, E and B. When the field E is switched off, the particle will move in a circular path of radius
AEBsBEsBCEsB2DEB2sA positive charge particle of mass m and charge q is projected with velocity v as shown in Fig. If radius of curvature of charge particle in magnetic field region is greater than d, then find the time spent by the charge particle in magnetic field.
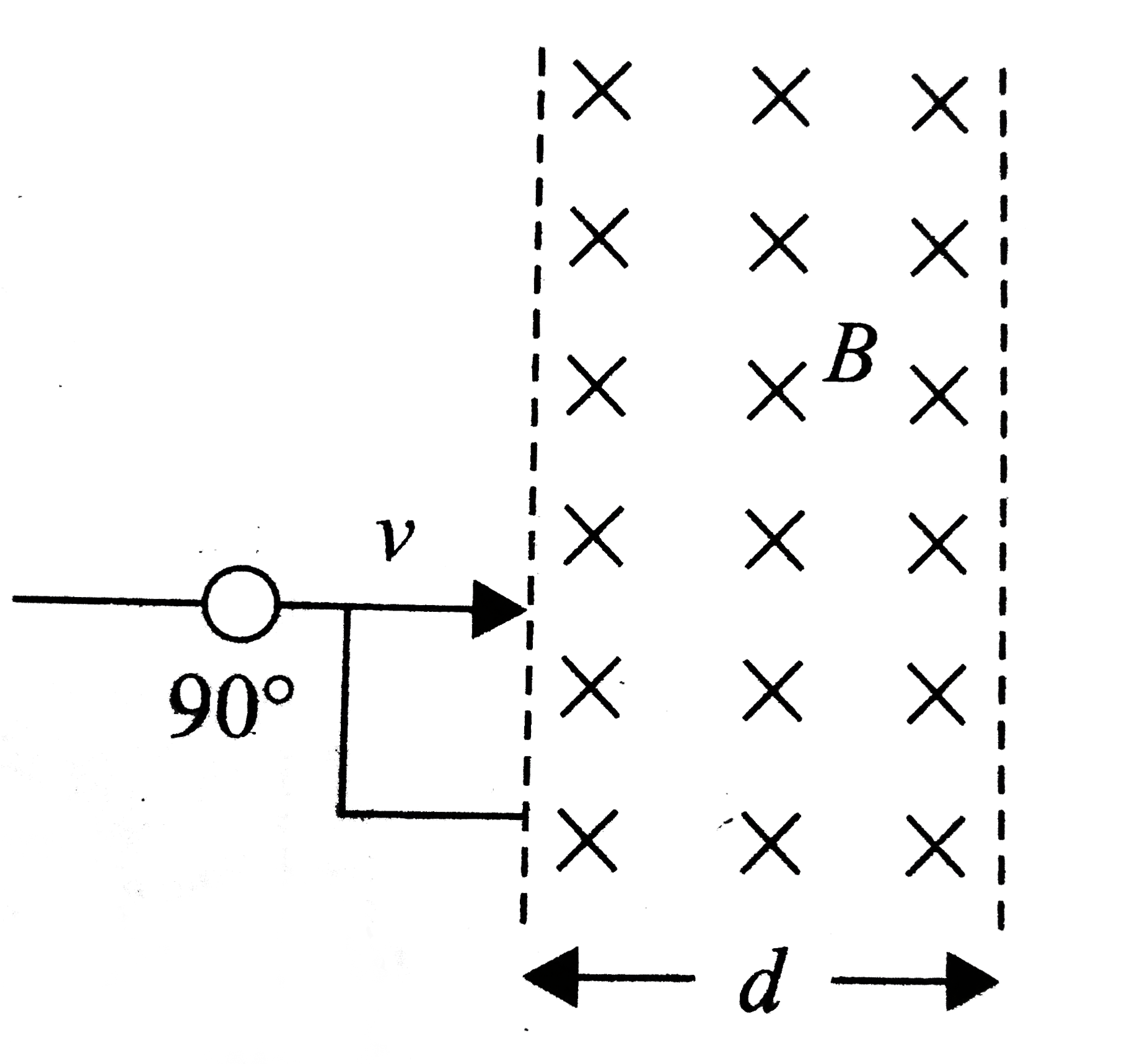 A2mqBsin−1(dqBmv)B2mqBsin−1(mvdqB)CmqBsin−1(dqBmv)DmqBsin−1(mvdqB)
A2mqBsin−1(dqBmv)B2mqBsin−1(mvdqB)CmqBsin−1(dqBmv)DmqBsin−1(mvdqB)A charged particle of charge q and mass m, gets deflected through an angle θ upon passing through a square region of side 'a' which contains a uniform magnetic field B normal to its plane. Assuming that the particle entered the square at right angles to one side, what is the speed of the particle ?
AqBmacot(θ)BqBmatan(θ)CqBmacot2(θ)DqBmatan2(θ)
A particle of mass ma and charge q has been projected from ground as shown in fig. Mark the correct statement(s) (xy) plane is vertical.

View SolutionA charged particle of specific charge α moves with a velocity →v=v0ˆi in a magnetic field →B=B0√2(ˆj+ˆk). Then (specific charge=charge per unit mass)
View SolutionA charged particle moves insides a pipe which is bent as shown in Fig. 1.151. If R<mvqB , then force exerted by the pipe on charged particle at P is (Neglect gravity)
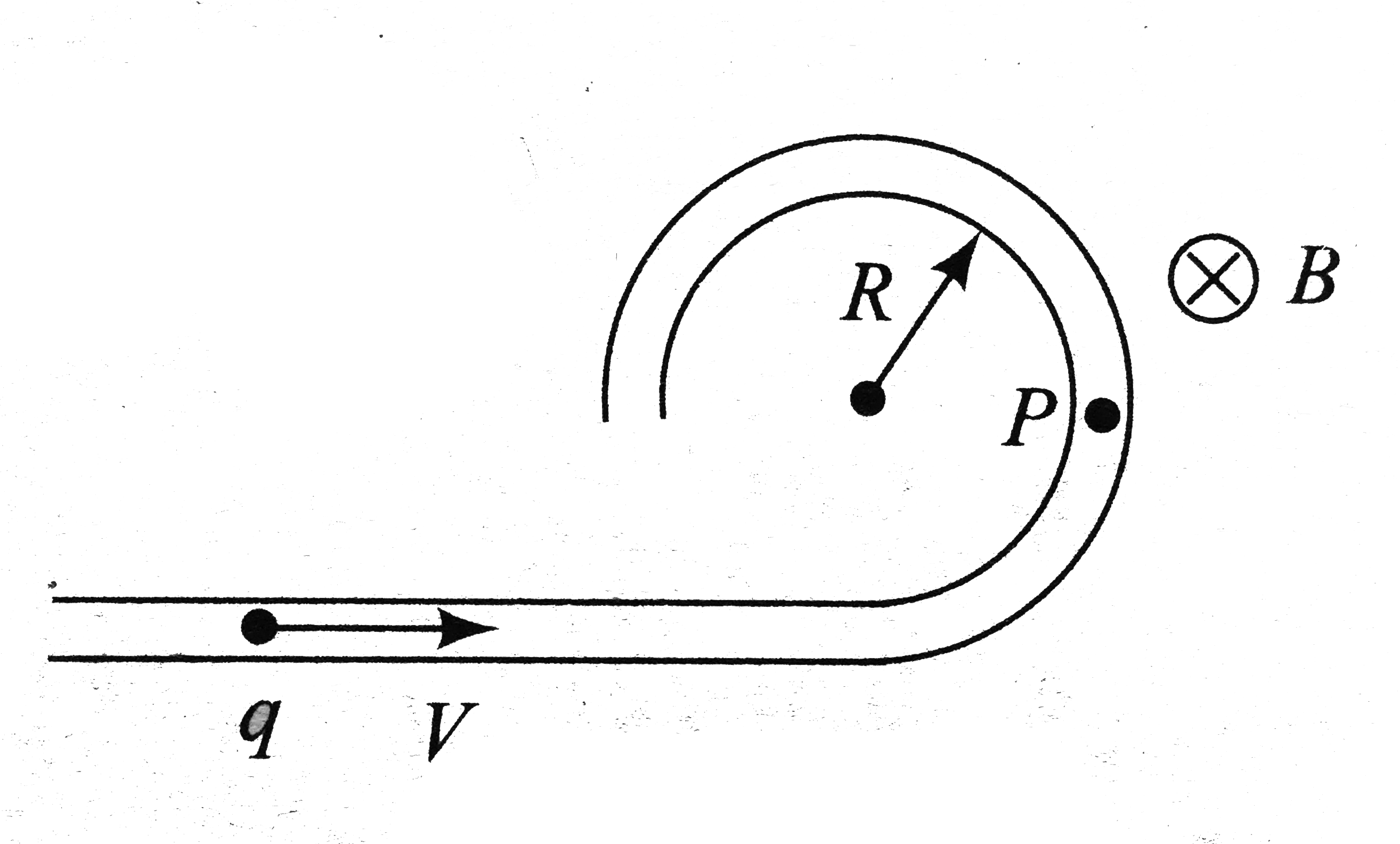
View SolutionA charged particle, having charge q1 accelerated through a potential difference V enter a perpendicular magnetic field region in which it experiences a force F. If V is increased to 5V, the particle will experience a force
View SolutionThere exist uniform magnetic field →B=−B0ˆk in region of space with 0<x<d and 2d<x<3d as shown in the figure. A positive charged particle of mass m and charge q is projected with velocity →v=vˆi as shown in the figure. If radius of curvature of path of the charged particle in magnetic field isR(2d<R<3d) then time elapse by charged particle in magnetic field regions is

View Solution
