Following experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.

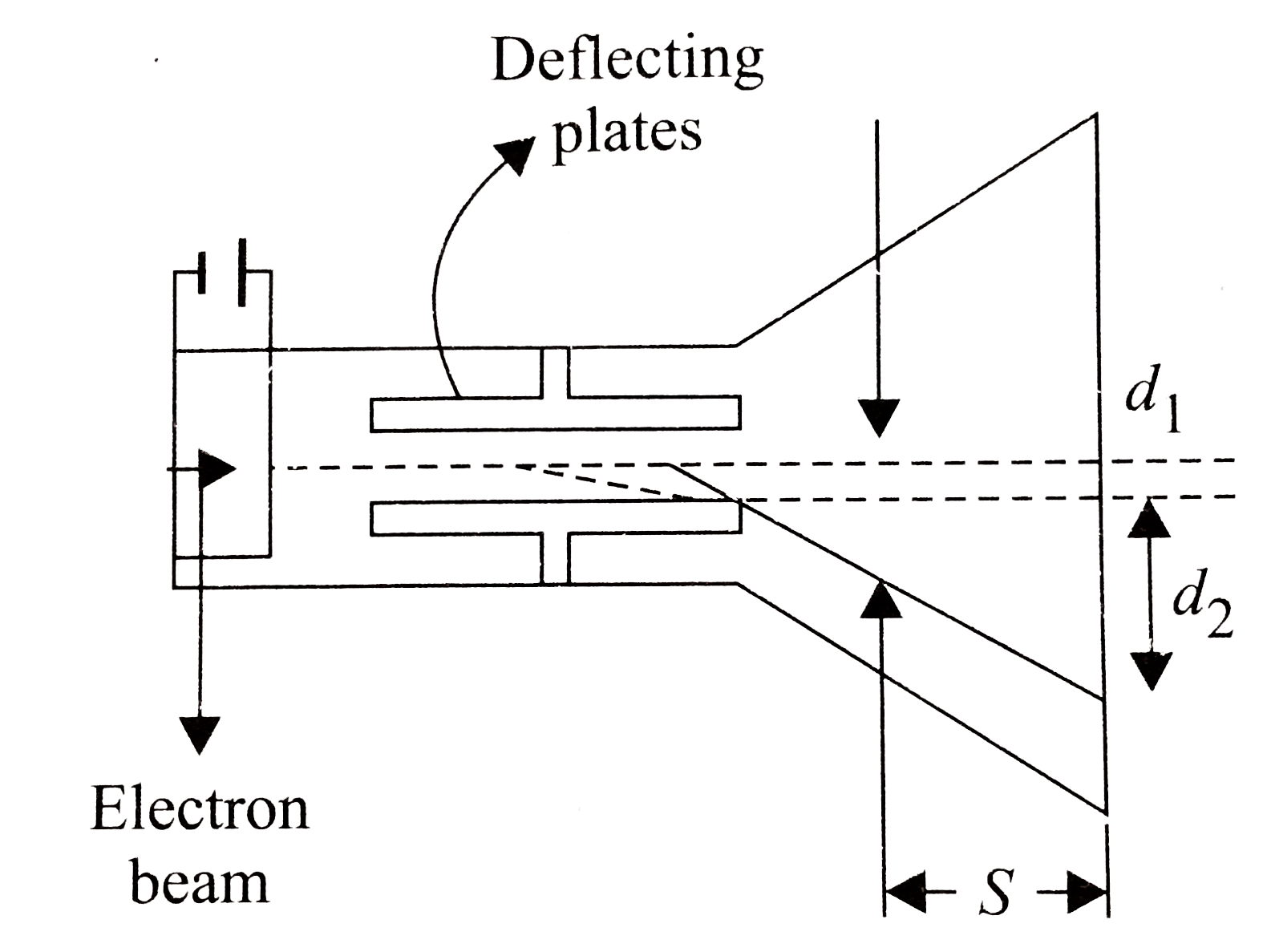
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by $d_{1} = \frac{e E L^{2}}{2 m V^{2}}$ where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE = evB. Using expression for $d_{1}$ we can find out $\frac{e}{m} = \frac{2 d_{1} E}{B^{2} L^{2}}$
If the electron is deflected downward when only electric field is turned on, in what direction do the electric and magnetic fields point in second part of experiment

The electric field point to the top, while the magnetic field point into the page

The electric field point to the top, while the magnetic field point out of page

Electric field points to the bottom, while the magnetic field point out of pate

Electric field points to the bottom, while the magnetic field points into the page

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Since electrons are deflected downward, hence electric field must be upward. The magnetic force in order to cancel the electric force must point upward. From right hand rule, magnetic field must point out of page. Hence choice (b) is correct.

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Following experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.

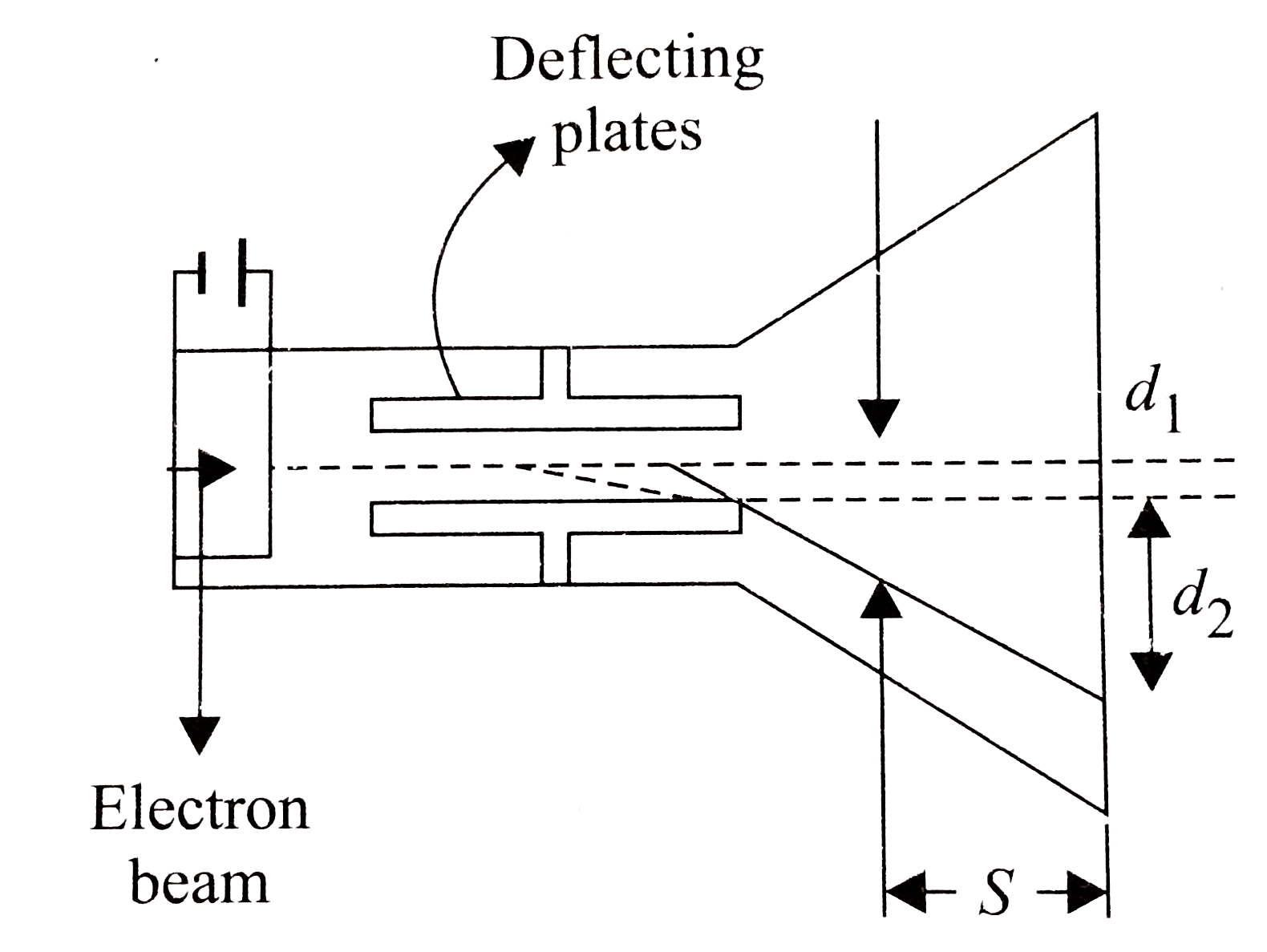
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by $d_{1} = \frac{e E L^{2}}{2 m V^{2}}$ where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives $e E = e v B$ . Using expression for $d_{1}$ we can find out $\frac{e}{m} = \frac{2 d_{1} E}{B^{2} L^{2}}$
If the electron speed were doubled by increasing the potential differece V, which of the following would be true in order to correctly measure $e / m$
AMagnetic field would have to be halved
BMagnetic field would have to be doubled
CLength L of the plates would have to be doubled
DLength L of the plates would have to be halved
Question 2 - Select One
Following experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.

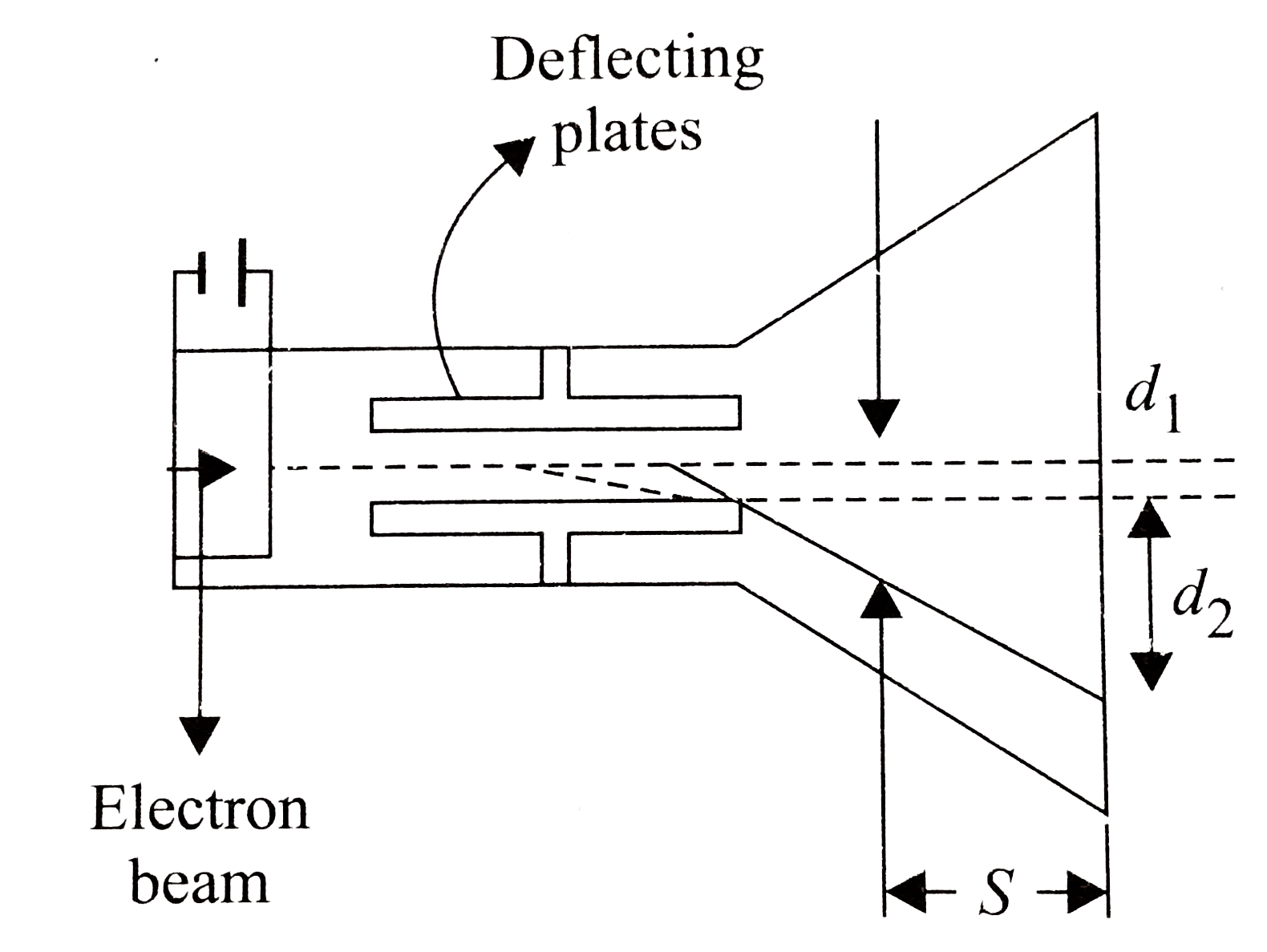
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by $d_{1} = \frac{e E L^{2}}{2 m V^{2}}$ where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives $e E = e v B$ . Using expression for $d_{1}$ we can find out $\frac{e}{m} = \frac{2 d_{1} E}{B^{2} L^{2}}$
A beam of electron with velocity $3 \times 10^{7} m s^{- 1}$ is deflected 2 mm while passing through 10 cm in an electric field of $1800 V / m$ perpendicular to its path. $e / m$ for electron is
A $1.5 \times 10^{11} C k g^{- 1}$
B $2 \times 10^{11} C k g^{- 1}$
C $2.5 \times 10^{11} C k g^{- 1}$
D $3 \times 10^{11} C k g^{- 1}$
Question 3 - Select One
The direction of a cathode ray particle passing through a magnetic field can by found by
AFleming's left hand rule
BLaplace's law
CMaxwell's cork screw rule
DAmpere's rule

CENGAGE PHYSICS-MISCELLANEOUS VOLUME 5-Linked Comprehension

Home
Ask Doubt
Profile

The correct Answer is:B

Since electrons are deflected downward, hence electric field must be upward. The magnetic force in order to cancel the electric force must point upward. From right hand rule, magnetic field must point out of page. Hence choice (b) is correct.

Topper's Solved these Questions

Similar Questions

Knowledge Check

The direction of a cathode ray particle passing through a magnetic field can by found by

CENGAGE PHYSICS-MISCELLANEOUS VOLUME 5-Linked Comprehension