ln a quadrilateral ABCD,−−→AC is the bisector of the (−−→AB∧−−→AD) which is 2π3,15∣∣∣−−→AC∣∣∣=2∣∣∣−−→AB∣∣∣=5∣∣∣−−→AD∣∣∣ then cos(−−→BA∧−−→CD) is
Step by step video & image solution for ln a quadrilateral ABCD, vec(AC) is the bisector of the (vec(AB) ^^ vec(AD)) which is (2pi)/3 , 15|vec(AC)| = 2 |vec(AB)| = 5|vec(AD)| then cos (vec(BA) ^^ vec(CD)) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
In a quadrilateral ABCD, −−→AB+−−→DC=
A−−→AB+−−→CBB−−→AC+−−→BDC−−→AC+−−→DBD−−→AD−−−→CBIn a quadrilateral ABCD. −−→AC is the bisector of −−→AB and −−→AD, angle between −−→AB and −−→AD is 2π/3 . 15∣∣∣−−→AC∣∣∣=3∣∣∣−−→AB∣∣∣=5∣∣∣−−→AD∣∣∣. Then the angle between −−→BA and −−→CD is.
Acos−1(√14)7√2Bcos−1(√21)7√3Ccos−1(2)√7Dcos−1(2√7)14If ABCDE is a pentagon, then
−−→AB+−−→AE+−−→BC+−−→DC+−−→ED+−−→AC is equal toA4−−→ACB2−−→ACC3−−→ACD5−−→AC
Given a parallelogram ABCD. If ∣∣∣−−→AB∣∣∣=a,∣∣∣−−→AD∣∣∣=b&∣∣∣−−→AC∣∣∣=c , then −−→DB.−−→AB has the value
View SolutionIf ABCD is a quadrilateral, then −−→BA+−−→BC+−−→CD+−−→DA=
View SolutionIf ABCDE is a pentagon, then
−−→AB+−−→AE+−−→BC+−−→DC+−−→ED+−−→AC is equal to
View Solution−−→ACand−−→BD are the diagonals of a parallelogram ABCD. Prove that
(i)−−→AC+−−→BD−2−−→BC
(ii) −−→AC−−−→BD−2−−→AB
View SolutionABCDEF is a regular hexagon, Fig. 2 (c ) .65. What is the value of
(−−→AB+−−→AC+−−→AD+−−→AE+−−→AF?
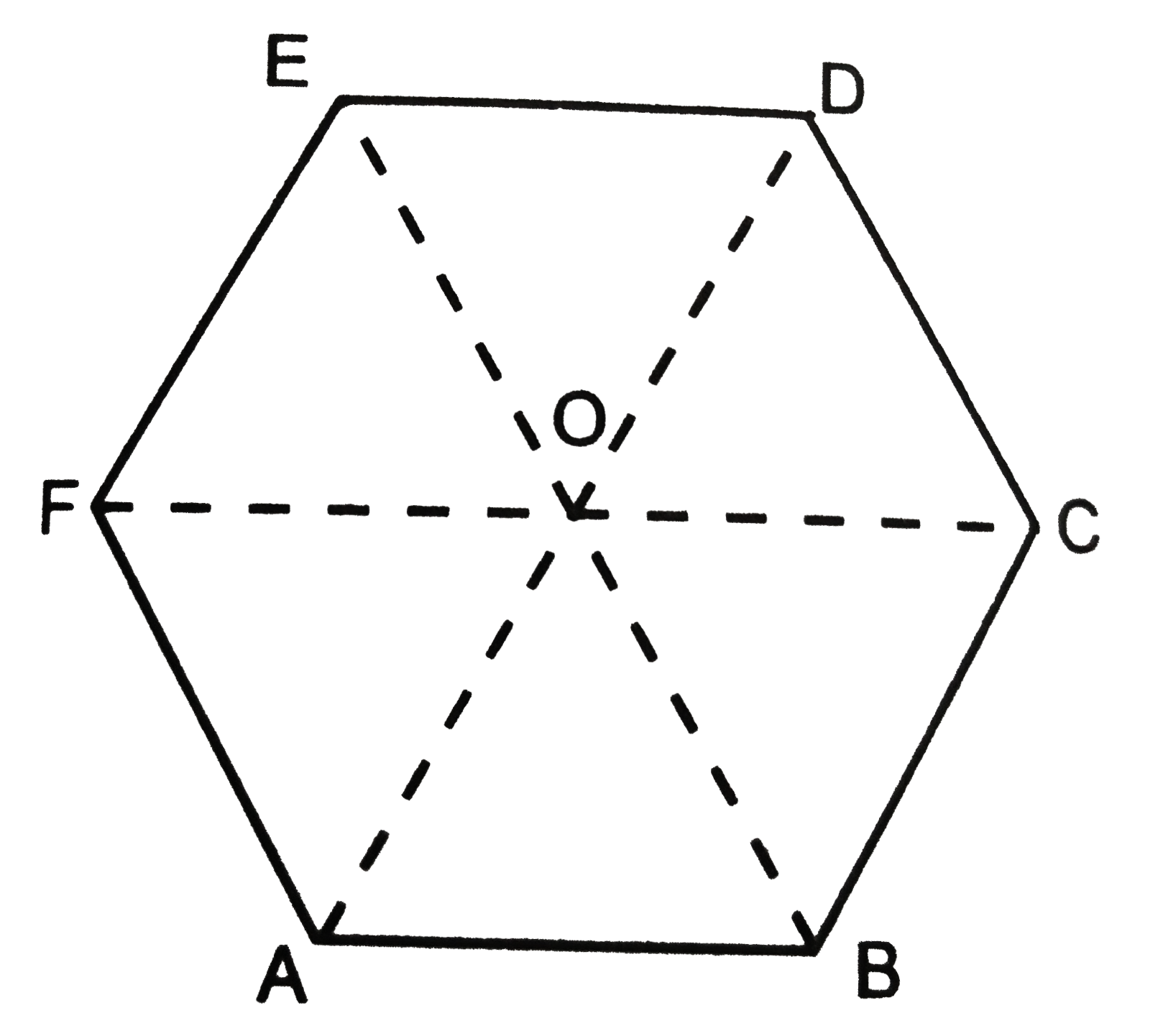 .
.
View Solution
