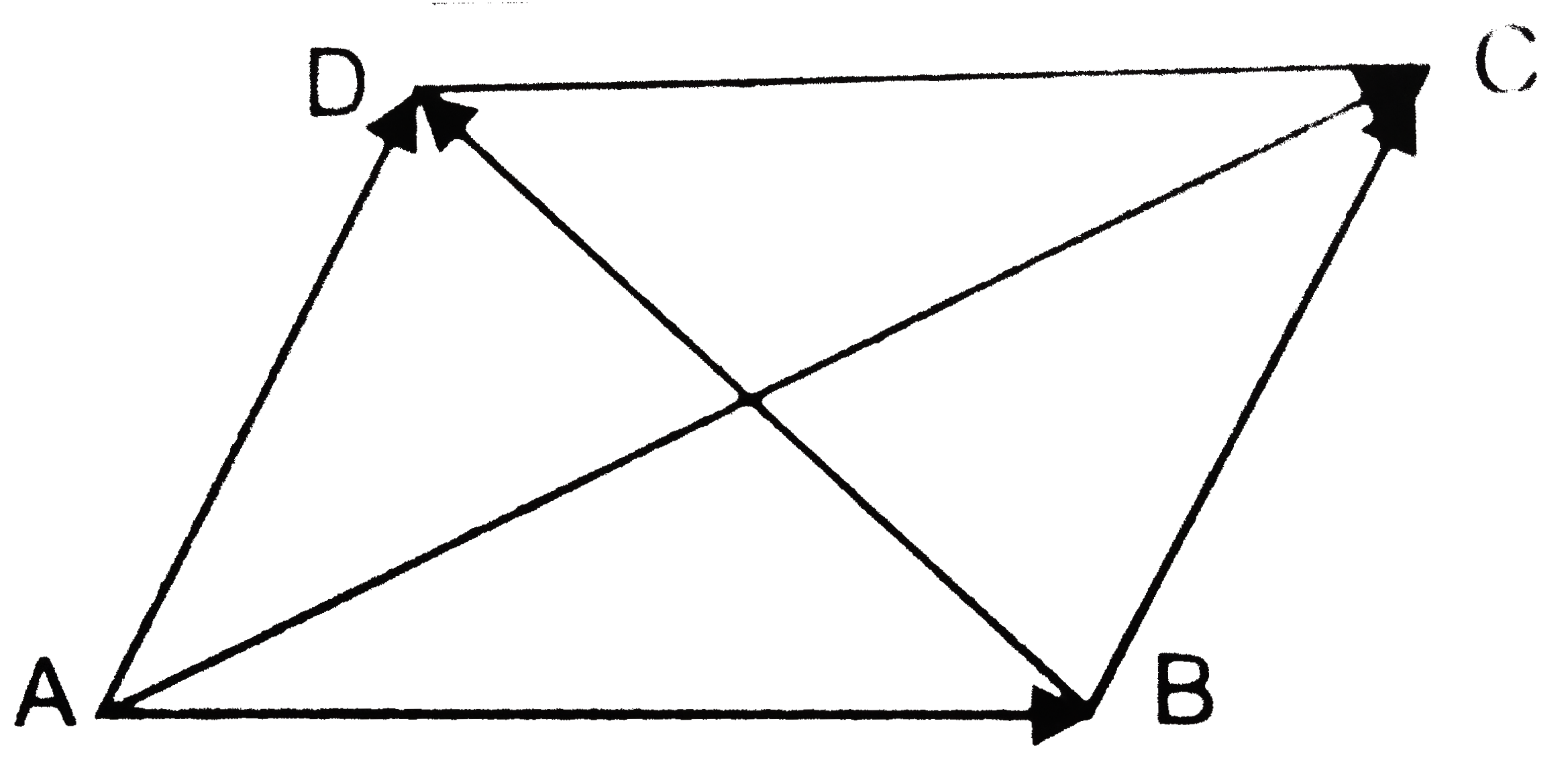
ABCD is a quadrilateral whose diagonals are AC and BD. Which one of the following is correct? (a) $\to B A + \to C D = \to A C + \to D B$ (b) $\to B A + \to C D = \to B D + \to C A$ (c) $\to B A + \to C D = \to A C + \to B D$ (d) $\to B A + \to C D = \to B C + \to A D$

Video Solution

Answer

Step by step video & image solution for ABCD is a quadrilateral whose diagonals are AC and BD. Which one of the following is correct? (a) vec BA + vec CD = vec AC + vec DB (b) vec BA + vec CD = vec BD + vec CA (c) vec BA + vec CD = vec AC + vec BD (d) vec BA+vec CD =vec BC + vec AD by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS INVERSE TRIGONOMETRIC FUNCTIONS

Knowledge Check

ABCD is a parallelogram with AC and BD as diagonals. Then, $A \to C - B \to D =$
A $4 A \to B$
B $3 A \to B$
C $2 A \to B$
D $A \to B$

If ABCD is a quadrilateral, then $- - \to B A + - - \to B C + - - \to C D + - - \to D A =$
View Solution
If $A B C D$ is quadrilateral and $E a n d F$ are the mid-points of $A C a n d B D$ respectively, prove that $\to A B + \to A D$ + $\to C B$ + $\to C D$ =4 $\to E F .$
View Solution
If ABCD is a quadrilateral, then the resultantof the forces represented by $- - \to B A, - - \to B C, - - \to C D and - - \to D A$ is
View Solution
The condition for equations $\to r \times \to a = \to b a n d \to r \times \to c = \to d$ to be consistent is $\to b . \to c = \to a . \to d$ b. $\to a . \to b = \to c . \to d$ c. $\to b . \to c + \to a . \to d = 0$ d. $\to a . \to b + \to c . \to d = 0$
View Solution
The condition for equations $\to r \times \to a = \to b a n d \to r \times \to c = \to d$ to be consistent is $\to b . \to c = \to a . \to d$ b. $\to a . \to b = \to \cdot \to d$ c. $\to b . \to c + \to a . \to d = 0$ d. $\to a . \to b + \to \cdot \to d = 0$
View Solution
$- - \to A C and - - \to B D$ are the diagonals of a parallelogram ABCD. Prove that
(i) $- - \to A C + - - \to B D - 2 - - \to B C$
(ii) $- - \to A C - - - \to B D - 2 - - \to A B$
View Solution
A, B be points with PV's $\to a, \to b$ . If the point C on OA is such that $2 \to A C = - - \to C O . - - \to C D$ is parallel to $\to O B$ and $\to C D = \to O B$ then $\to A D$
View Solution

ABCD is a quadrilateral whose diagonals are AC and BD. Which one of the following is correct? (a) $\to B A + \to C D = \to A C + \to D B$ (b) $\to B A + \to C D = \to B D + \to C A$ (c) $\to B A + \to C D = \to A C + \to B D$ (d) $\to B A + \to C D = \to B C + \to A D$

Similar Questions

Knowledge Check

ABCD is a parallelogram with AC and BD as diagonals. Then, $A \to C - B \to D =$

Recommended Questions

ABCD is a quadrilateral whose diagonals are AC and BD. Which one of the following is correct? (a) →BA+→CD=→AC+→DB (b) →BA+→CD=→BD+→CA (c) →BA+→CD=→AC+→BD (d) →BA+→CD=→BC+→AD

Similar Questions

Knowledge Check

ABCD is a parallelogram with AC and BD as diagonals. Then, A→C−B→D=

Recommended Questions

ABCD is a quadrilateral whose diagonals are AC and BD. Which one of the following is correct? (a) $\to B A + \to C D = \to A C + \to D B$ (b) $\to B A + \to C D = \to B D + \to C A$ (c) $\to B A + \to C D = \to A C + \to B D$ (d) $\to B A + \to C D = \to B C + \to A D$

ABCD is a parallelogram with AC and BD as diagonals. Then, $A \to C - B \to D =$