
The rectangular plate shown if Fig. 1.7 has an area Ai. If the temperature increases by ΔT, each dimension increases according to ΔL=αLΔT, where α is the average coefficient of linear expansion. Show that the increase in area is ΔA=2αAiΔT. What approzimation does this expansion assume?

We expect the area to increase in thermal expansion. It is neat that the coefficent of area expansion is just twice the coefficient of linear expansion. We will use the definitions of coefficients of linear and area expansion.
From the diagram is Fig. 1.8, we see that the change in area is
ΔV=lΔw+wΔl+ΔwΔl
Since Δl and Δw are each small quantities, the product ΔwΔl will be very small as compared to the original or final area.
Therefore, we assume ΔwΔl∝0
Since Δw=wαΔT and Δl=lαΔT
We then have ΔA=lwαT+wlαΔT
Finally, since A=lw, we have ΔA=2αAΔT
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Exercise 1.123videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Exercise 1.222videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.620videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE1videos
CENTRE OF MASS
Similar Questions
When the temperature of a rod increases from 1 to t. Delta t,the moment of inertia increases from 1 to 1+Delta.The coefficient of linear expansion of the rod is alpha.The ratio Delta I/I is :
View SolutionTwo rods of different materials but having same length L and cross-sectioinal areas A are arranged end-to-end between fixed supports. The temperature is T and there is no initial stress. The rods are heated so that their temperature increases by ΔT. Find : (a) the displacement of the interface (b) the stress at the interface. The coefficinets of linear expansioin of the materials are α1 and α2 and their Young's modulii are E1 and E2 respectively.
View Solution
Knowledge Check
- Question 1 - Select One
The moment of ineratia of a uniform thin rod about its perpendicular bisector is I. If the temperature of the rod is increased by Δt , the moment of inertia about perpendicular bisector increases by (coefficient of linear expansion of material of the rod is α).
AZeroBIαΔtC2IαΔtDIαΔt - Question 2 - Select One
A cube of edge (L) and coefficient of linear expansion (α) is heated by 10C. Its surface area increases by
A6αL2B8αL2C12αL2D2αL2 - Question 3 - Select One
A thread of liquid is in a uniform capillary tube of length L. As measured by a ruler. The temperature of the tube and thread of liquid is raised by ΔT. If γ be the coefficient of volume expansion of the liquid and α be the coefficient of linear expansion of the material of the tube, then the increase ΔL in the length of the thread, again measured by the ruler will be
AΔL=L(γ−α)ΔTBΔL=L(γ−2α)ΔTCΔL=L(γ−3α)ΔTDΔL=LγΔT
Imagine a hypothetical material whose average temperature coefficient of linear expansion is 0.1/.∘C .Find the fractional increase in area of thin square plate of above material when temperature is increase by 10∘C
View SolutionA rectangular tank contains water to a height h. A metal rod is hinged to the bottom of the tank so that it can rotate freely in the vertical plane. The length of the rod is L and it remains at rest with a part of it lying above the water surface. In this position the rod makes an angle θ with the vertical. Assume thaty=cosθ and find fractional change in value of y when temperature of the system increases by a small value ΔT.Coefficient of linear expansion of material of rod and the tank areα1 and α2 respectively. Coefficient of volume expansion of water is λ. What is necessary condition for θ to increase?
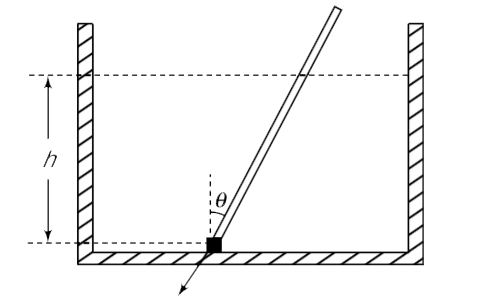 View Solution
View SolutionTwo rods of material X sandwich another rod of material Y as shown in figure. At temperature t, the three rods are in a state of zero strailn and of length L and riveted to each other in this state. If the temperature of the system increases to T+ΔT, find the final length of the system of the three rods. Given that the coefficients of linear expansions of the roods and their Young's modulus for material X and Y are alpnax,αy,Yx and Yy respectively. Consider αy>αx.
 View Solution
View SolutionA semi circular disc of radius R is placed on a smooth horizontal surface. Figure shows top view of this. If temperature is increased by Δt then displacement of (coefficient of linear expansion is α):
 View Solution
View SolutionWhen solid is heated , its length changes according to the relation l=l0(1+αΔT) , where l is the final length , l0 is the initial length , ΔT is the change in temperature , and α is the coefficient of linear is called super - facial expansion. the area changes according to the relation A=A0(1+βΔT), where A is the tinal area , A0 is the initial area, and β is the coefficient of areal expansion.
A metal disc having a circular hole at its center is heated . If the metal expands on heating , the diameter of the holeView Solution

