A rectangular tank contains water to a height h. A metal rod is hinged to the bottom of the tank so that it can rotate freely in the vertical plane. The length of the rod is L and it remains at rest with a part of it lying above the water surface. In this position the rod makes an angle θ with the vertical. Assume thaty=cosθ and find fractional change in value of y when temperature of the system increases by a small value ΔT.Coefficient of linear expansion of material of rod and the tank areα1 and α2 respectively. Coefficient of volume expansion of water is λ. What is necessary condition for θ to increase?
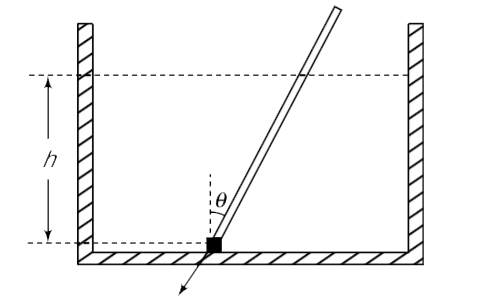
The correct Answer is:12(α1+γ−4α2)ΔT;4α2>α1+γ
Topper's Solved these Questions
Similar Questions
A slender uniform rod of mass M and length l is pivoted at one end so that it can rotate in a vertical plane, Fig. There is negligible friction at the pivot. The free end is held vertically above the pivot and then released. The angular acceleration of the rod when it makes an angle θ with the vertical is
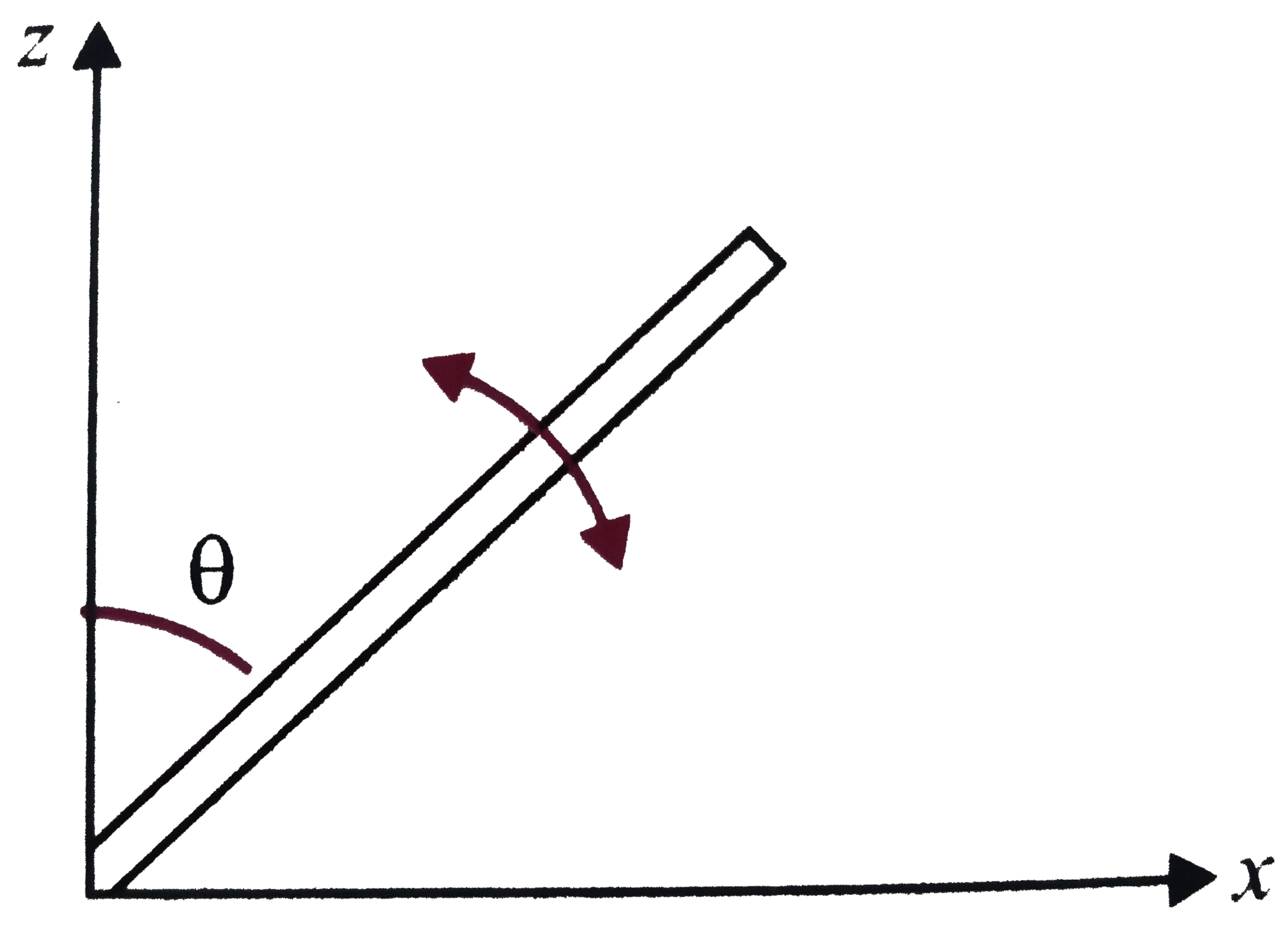
View SolutionA rod AB of length L slides in the XY plane. If the rod makes an angle θ with the vertical, the angular velocity of the rod can be found by an expression which is
View Solution
Knowledge Check
A slender uniform rod of mass M and length l is pivoted at one ens so that it can rotate in a vertical plane, Fig. There is negligible friction at the pivot. The free end is held vertically above the pivot and then released. The angular acceleration of the rod when it makes an angle θ with the vertical is
 A3g2lcosθB2g3lcosθC3g2lsinθD2g3lsinθ
A3g2lcosθB2g3lcosθC3g2lsinθD2g3lsinθA steel rod of length L, density d and cross-sectional area A, is hinged at one end so that it can rotate freely in a vertical plane. The rod is released from a horizontal position. When it becomes vertical, the stress at its midpoint is
A13dLg8B12dLg8C2dLg5DdLg2A steel rod of length L, density d and cross-sectional area A, is hinged at one end so that it can rotate freely in a vertical plane. The rod is released from a horizontal position. When it becomes vertical, the stress at its midpoint is
A13dLg/8B12dLg /8C2dL g/5DdLg/2
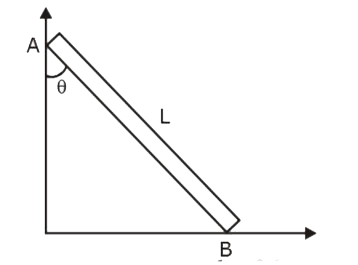
A light rigid rod of length l is constrained to move in a vertical plane, so that its ends are along the x and y axes respectively. Find the instantaneous axis of rotation of the rod when it makes an angle θ with horizontal.
View SolutionA light rigid rod of length l is constrained to move in a vertical plane, so that its ends are along the x and y axes respectively. Find the instantaneous axis of rotation of the rod when it makes an angle θ with horizontal.
View SolutionA rod of mass m and length L is pivoted at the bottommost point O and can freely rotate about the point O. The rod is disturbed from the vertical position so that it starts rotating about O. When it makes an angle θ with the vertical
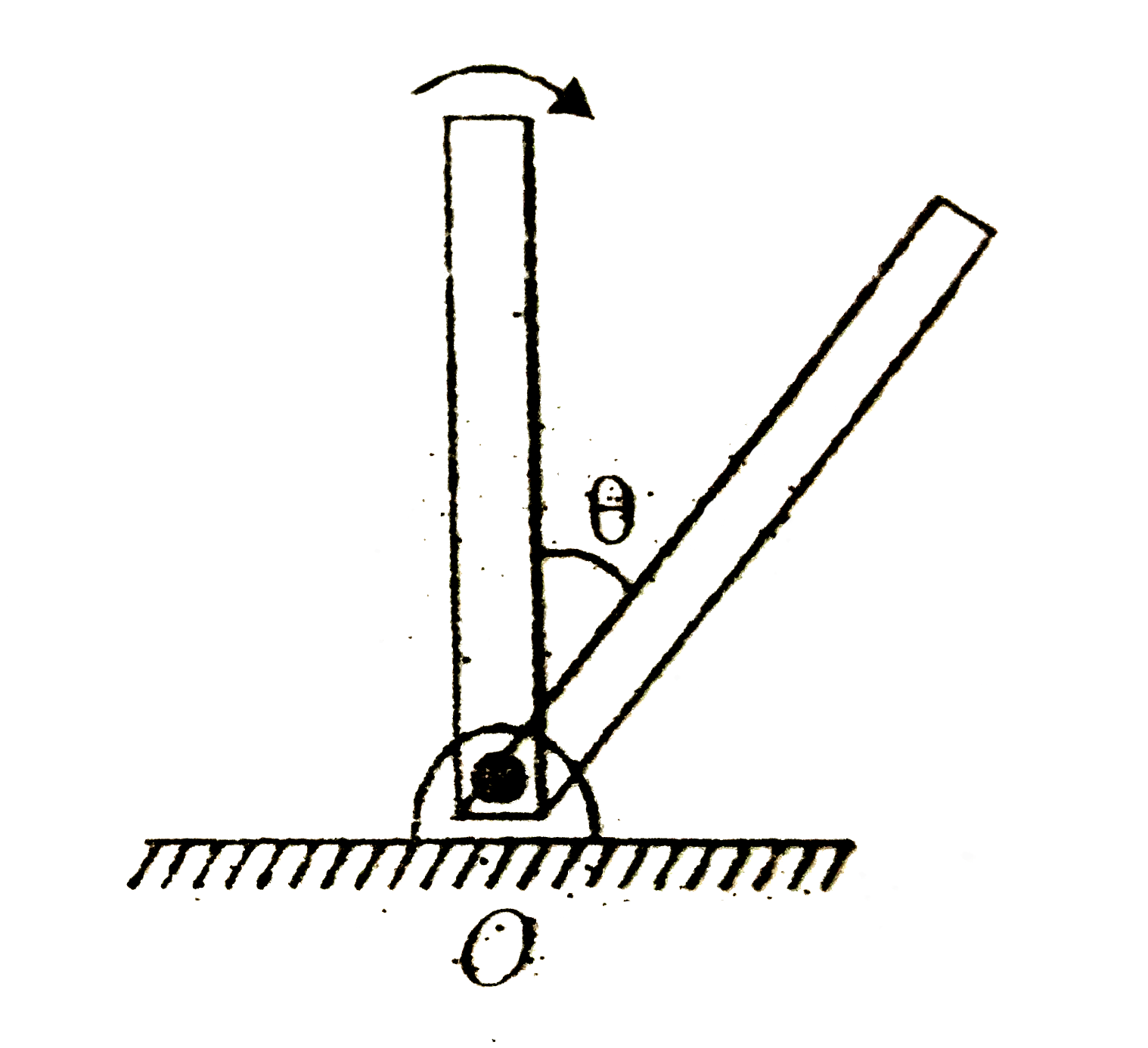
View SolutionA rod of mass m and length L is pivoted at the bottommost point O and can freely rotate about the point O. The rod is disturbed from the vertical position so that it starts rotating about O. When it makes an angle θ with the vertical
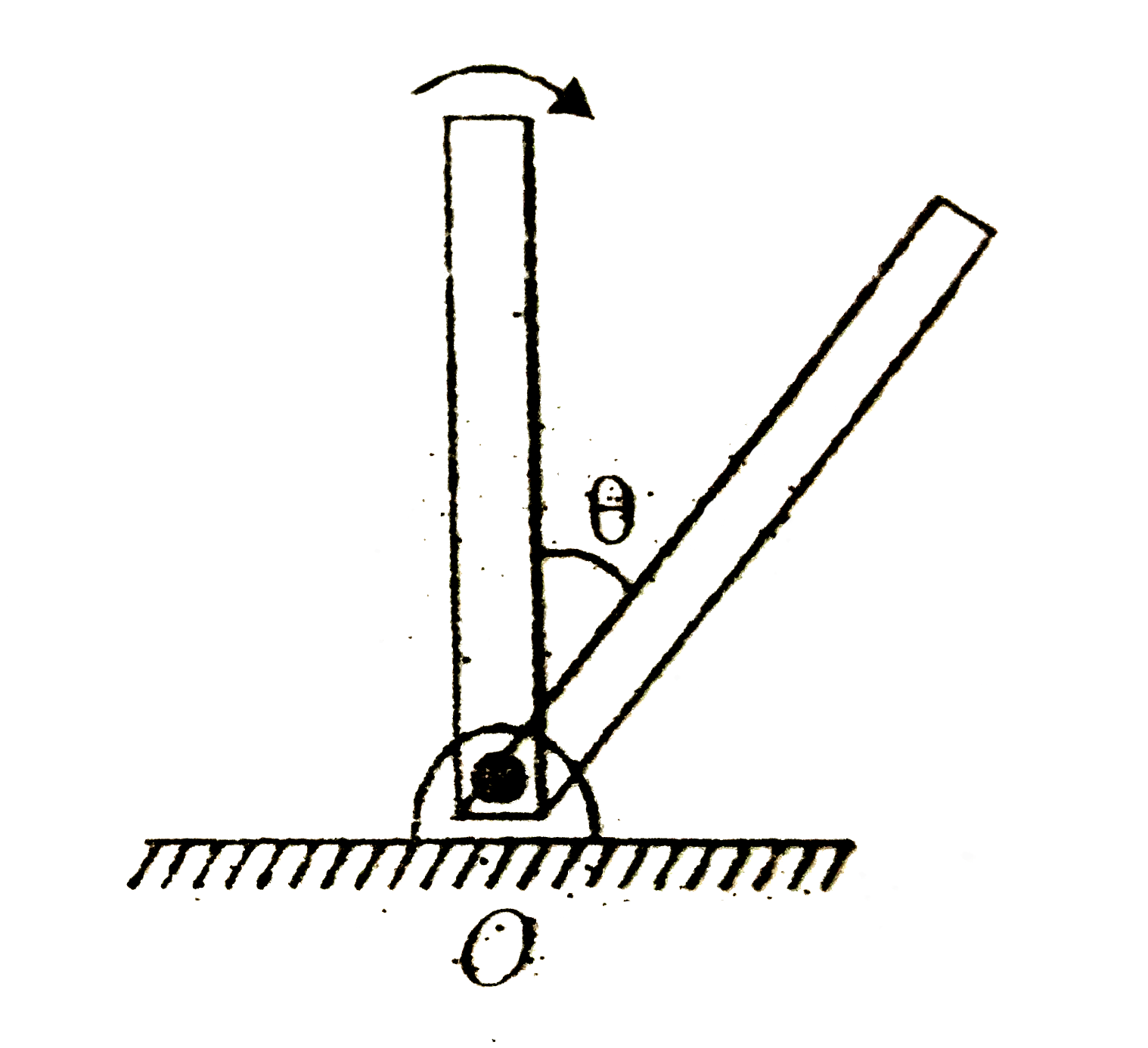
View SolutionA uniform rod of density ρ is placed in a wide tank containing a liquid of density ρ0(ρ0>ρ). The depth of liquid in the tank is half the length of the rod. The rod is in equilibrium, with its lower end resting on the bottom of the tank. In this position the rod makes an angle θ with the horizontal.
View Solution
