A particle of mass $2 k g$ is moving of a straight line under the actin force $F = (8 - 2 x) N$ . It is released at rest from $x = 6 m$ .
a. Is the particle moving simple hormonically.
b. Find the equilibrium position of the particle.
c. Write the equation of motion of the particle.
d. Find the time period of SHM.

Video Solution

Text Solution

Verified by Experts

$f = 8 - 2 x$
or $F = - 2 (x - 4)$
For equilibrium position $F = 0$
$\Rightarrow x = 4$ is equilibrium position
Hence the motion of the partuical is SHM with force canstant 2 and equilibrium position $x = 4$ .
a. Yes, motion is SHM.
b. Equilibrium position $x = 4$ .

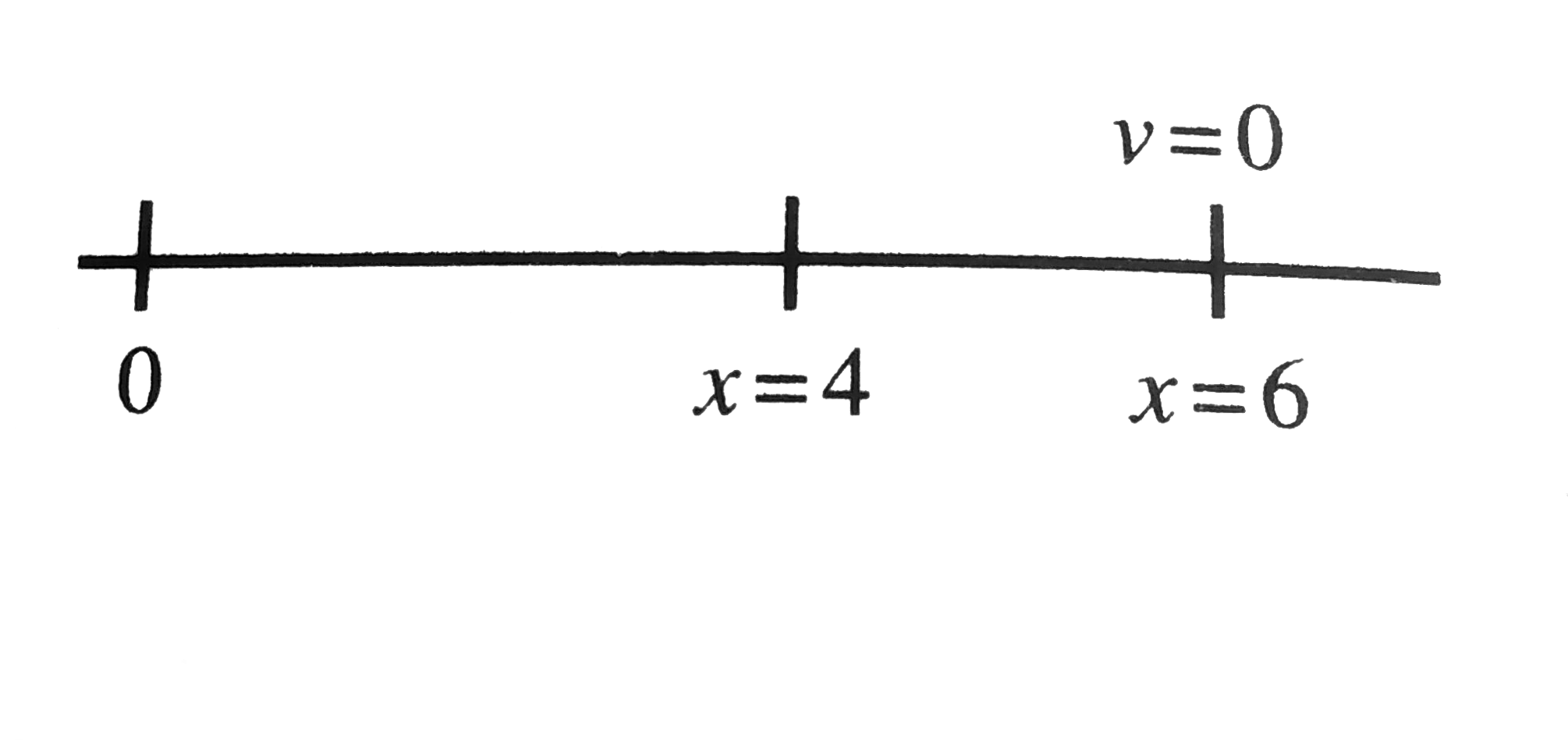
c. At $x = 6 m$ partical is at rest, i.e. it is one of the extreme position.
Hence amplitude is $A = 2 m$ and initially partical is at the exterme position.
$∴$ Equation of Shm can be written as
$x - 4 = 2 cos ω t$
where $ω = \sqrt{\frac{k}{m}}$
$= \sqrt{\frac{2}{2}} = 1$
i.e., $x = 4 + 2 cos t$
d. The time period
$T = \frac{2 π}{ω} = 2 π s$

Updated on:21/07/2023

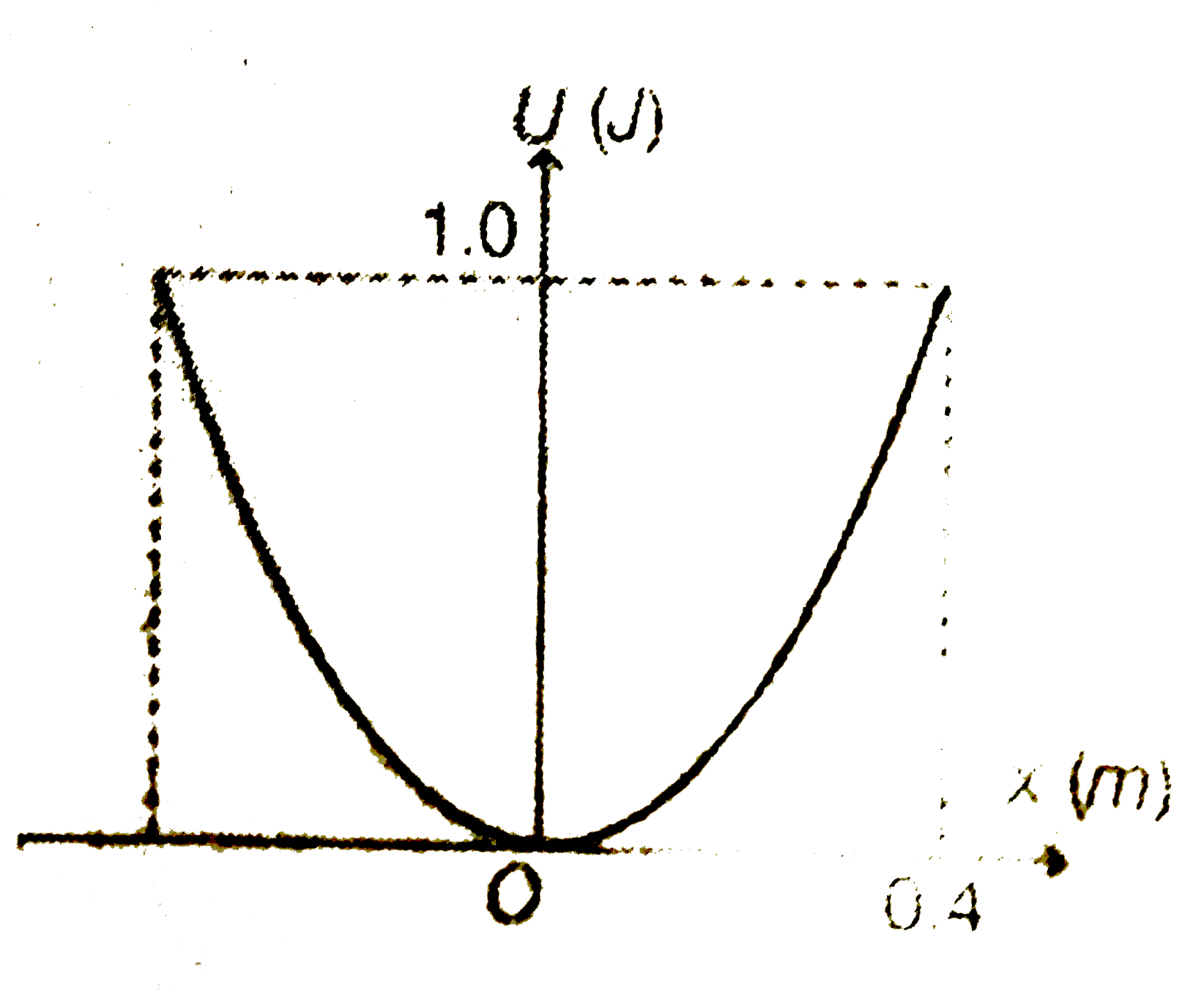
A particle of mass $2 k g$ moves in simple harmonic motion and its potential energy $U$ varies with position $x$ as shown. The period of oscillation of the particle is

A $\frac{2 π}{5} s$
B $2 \frac{\sqrt{2 π}}{5} s$
C $\frac{\sqrt{2 π}}{5} s$
D $\frac{4 π}{5} s$
Force acting on a particle of mass m moving in straight line varies with the velocity of the particle as $F = K / V$ K is constant then speed of the particle in time t
A $\sqrt{\frac{k t}{m}}$
B $\sqrt{\frac{2 k t}{m}}$
C $2 \sqrt{\frac{k t}{m}}$
Dnone of these