
A block A is connected to spring and performs simple harmonic motion with a time period of 2 s. Another block B rests on A. The coefficient of static friction between A and B is μS=0.6. The maximum amplitude of oscillation which the system can have so that there is no relative motion between A and B is (take π2=g=10)
0.3 m
0.6 m
0.4 m
0.52 m
The correct Answer is:B

Let A be the maximum amplitude of oscillation for the required situation. Then f=mω2x (from free body diagram of blocks)
For required condition f=mω2A
i.e., mω2A<μSmg
⇒A<0.6×g4π24=0.6m⇒Amax=0.6m
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
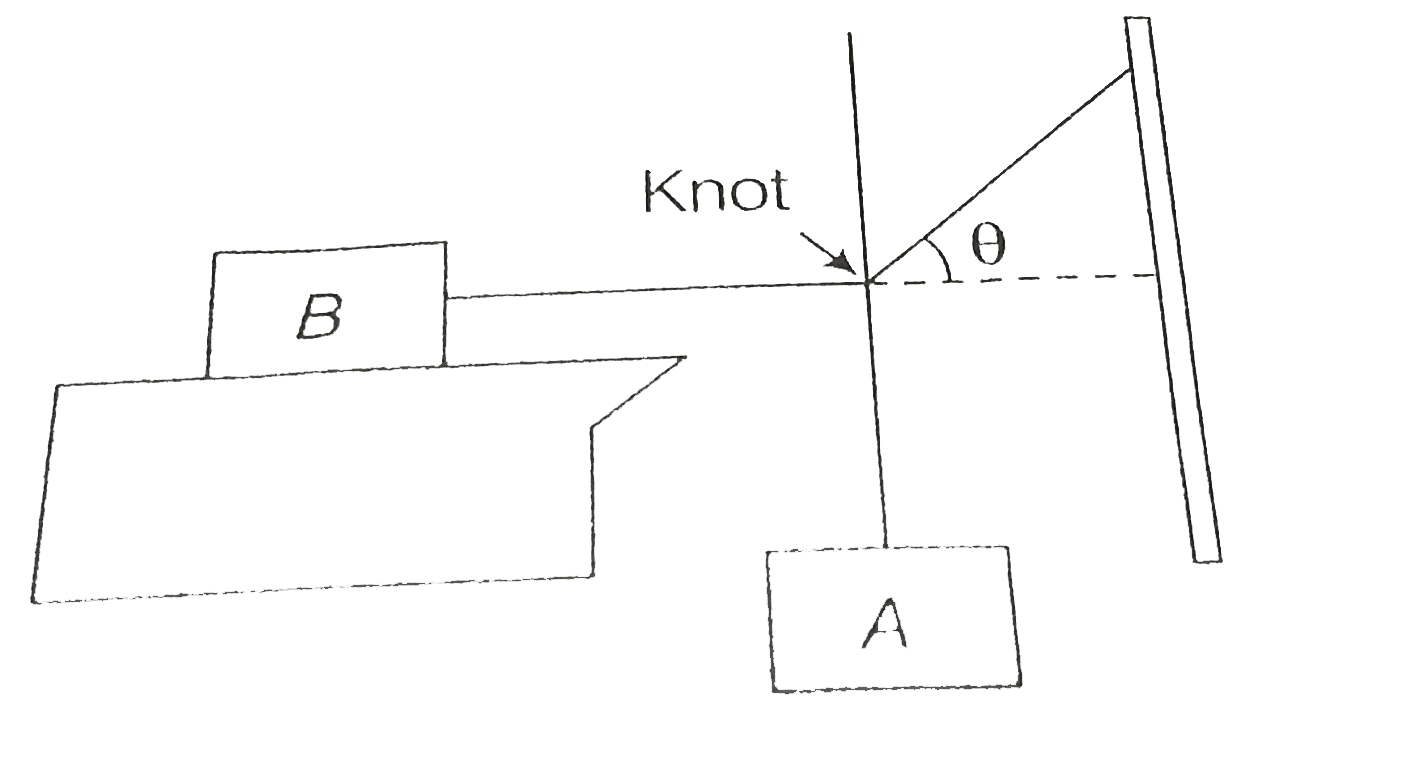
Block B lying on a table weighs w. The coefficient of static friction between the block and the table is mu. Assume that the cord between B and the knot is horizontal. The maximum weight of the block A for which the system will be stationary is
View SolutionBlock B rests on surface . If the coefficient of static friction between A and B is μ=0.4. Determine the acceleration of each , if
(a) F=30N and
(b) F=250N(g=10m/s2)

View Solution
Knowledge Check
Block B rests on a smooth surface .The coefficient of static friction between A and B is μ=0.4 where F=30N then
Acceleration of lower block is
 A3/7ms−2B4/3ms−2C6/7ms−2D3/2ms−2
A3/7ms−2B4/3ms−2C6/7ms−2D3/2ms−2Block B rests on a smooth surface .The coefficient of static friction between A and B is μ=0.4 where F=30N then

Acceleration of upper block isA3/2ms−2B6/7ms−2C4/3ms−2D3/7ms−2A block on a horizontal slab is moving horizontally with a simple harmonic motion of frequency two oscillations per second. If the coefficient of static friction between block and slab is 0.5, then the amplitude of the oscillation will be (if the block does not slip along the slab)
A3.3 cmB3.5 cmC3.15 cmD7 cm
A block is kept on a horizontal table that is executing simple harmonic motion of frequency v in the horizontal plane. The coefficient of static friction between the block and the table is μ. Determine the maximum amplitude of the table for which the block does not slip on the surface of the table.
View SolutionA block is kept on a horizontal table. The table is undergoing simple farmonic motion of frequency 3Hz in a horizontal plane. The coefficient of static friction between the block and the table surface is 0.72. find the maximum amplitude of the table at which the block does not slip on the surface g=10ms−1
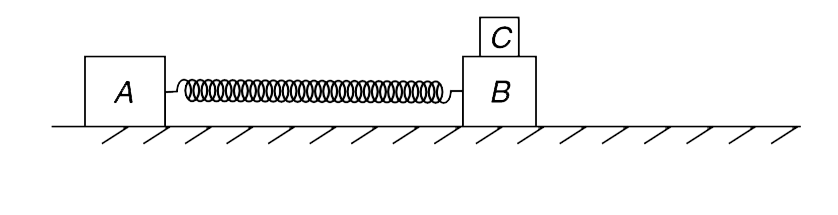
View SolutionTwo block A and B are connected to a spring (force constant k = 480 N/m) and placed on a horizontal surface. Another block C is placed on B. The coefficient of friction between the floor and block A is μ1=0.5, whereas there is no friction between B and the floor. Coefficient of friction between C and B is μ2=0.85. Masses of the blocks are MA=50kg,MB=28 kg and MC=2kg. The system is held at rest with spring compressed by x0=0.5m. After the system is released, find the maximum speed of block B during subsequent motion.
View SolutionThe coefficient of static friction between two blocks is 0.5 and the table is smooth. The maximum horizontal force that can be applied to move the blocks together is N. (take g=10ms−2)

View Solution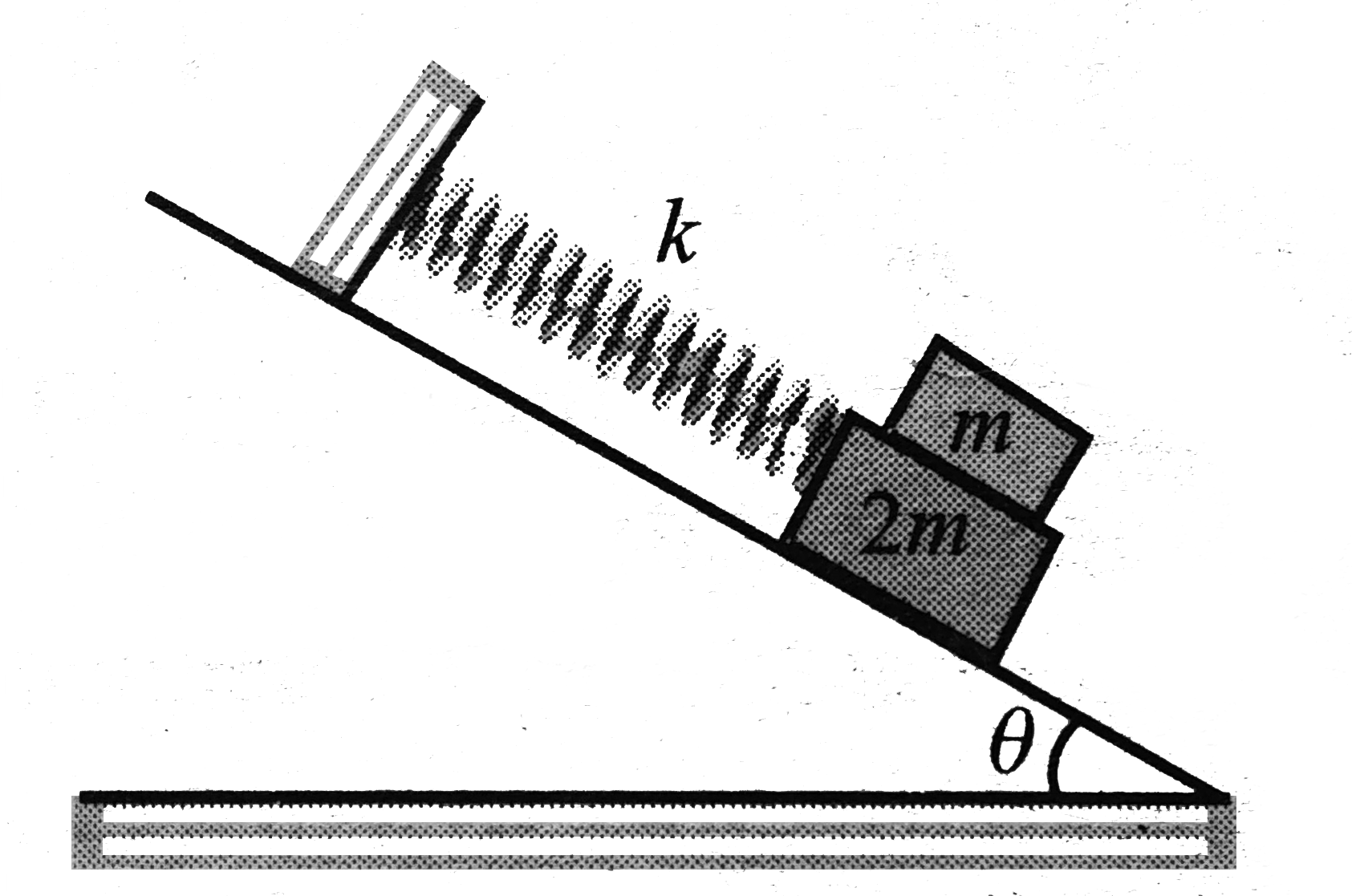
The coefficient of friction between block of mass m and 2m is μ=2tanθ. There is no friction between block of mass 2 m and inclined plane. The maximum amplitude of the two block system for which there is no relative motion between both the blocks is
View Solution
