(a) writ the expression for y as a function of x and t for a sinusoidal wave travelling along a rope in the neagative x direction with the folllowing characteristics: A =8.00 cm , δ=80.0cm,f=3.00Hz, and y(0,t)=0att=0, (b) write an expression for y as a function of x and t for the wave in part (a) assuming that y(x,0)=0 at the point x=10.0 cm.
Think about the graph of y as a function of x at one instant as a smoooth succession of identical crests and troughs, with the length in space of each cycle being 80.0cm. the distance from the top of a crest to the bottom of a trough is 16.0cm. now think of the whole graph moving towards the left at 240 cm/s.
using the travelling wave model, we can put constant with the right values into y=Asin(kx+ωt+ϕ) to have the mathetical representation of the wave. we have the same (positive) sings for both kx and omega t so that a point of constant phase will be at a decreasing value of x as t increase that is, so that the wave will move will move to the left.
The amplitude is A=ymax=8.00cm=0.0800m
The wave number is
k=2πλ=2π0.800m=5x2
the angular frequency, ω=2πf=2π(3.00s−1=6.00πrad/s
(a) we have y=Asin(ks+ωt+ϕ), choosing ϕ=0 will make it true that y(0,0)=0. then the wave function becomes upon sustitution of the constant value for this wave
y=(0.080m)sin(5π2x+6.00πt)
(b) in general, y=(0.0800m)sin(5π2x+6.00πt+ϕ) If y(x,0)=0atx=0.100m, we require
0=(0.0800m)sin(52π×0.1+ϕ)
5π2×0.1+ϕ=0
so we must have the phase constant ϕ=−π4rad therefore, the wave function for all values of the variable x and t is
yπ(0.0800m)sin(52πxπ6.00πt−π4)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Example9videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.19videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct9videos
TRANSMISSION OF HEAT
- BOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
A sinusoidal wave trsvelling in the positive direction on a stretched string has amplitude 2.0cm, wavelength 1.0cm and velocity 5.0m/s. At x=0 and t=0 it is given that y=0 and ∂y∂t<0. Find the wave function y(x,t).
View SolutionFind out the expression of wave equation which is moving is
+vex direction and at x=0,t=0y=A√2View Solution
Knowledge Check
- Question 1 - Select One
A wave is represented by the equation y=0.5sin(10t−x)m. It is a travelling wave propagating along the + x direction with velocity
A10m/sB20m/sC5m/sDNone of these - Question 2 - Select One or More
The equation of a transverse wave travelling along a spring is y=4.0sinπ(2.0t−0.010x) , where y and x are in cm and t in second
AAmplitude , a=4 cm, wavelength λ=200cm and frequency of the wire v=1s−1BThe initial phase at the origin is 180∘CThe phase difference between two positions of the same particle at a time interval of 0.50 second is 180°DNone of these - Question 3 - Select One
The wave described by y=0.25sin(10πx−2πt). Where x and y are in metre and t is second, is a wave travelling along the
A−ve x direction with frequency 1HzB+ve x direction with frequenc πHz and wavelength λ=0.2mC+ve x direction with frequency 1Hz and wavelength λ=0.2mD−ve x direction with amplitude 0.25m and wavelength λ=0.2m
A sinusoidal wave travelling in the positive x direction has an amplitude of 15 cm, wavelength 40 cm and frequency 8 Hz. The vertical displacement of the medium at t =0 and x = 0 is also 15 cm, as shown
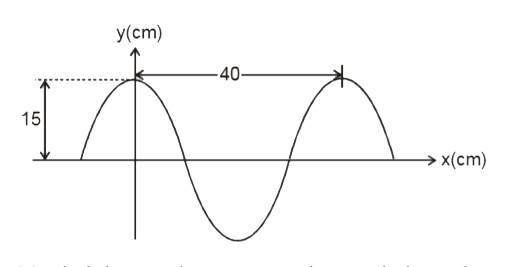
(b) Determine the phase constant ϕ, and write a general expression for the wave function.View SolutionA sinusoidal wave travelling in the positive x direction has an amplitude of 15 cm, wavelength 40 cm and frequency 8 Hz. The vertical displacement of the medium at t =0 and x = 0 is also 15 cm, as shown
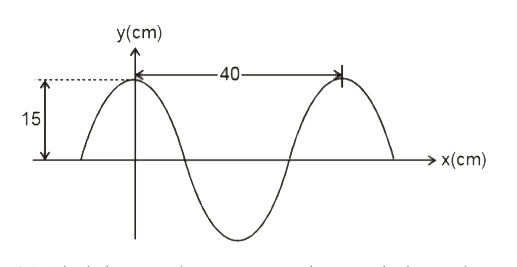
(a) Find the angular wave number, period angular frquency and speed of the wave.View SolutionShows a snapshot of a sinusoidal travelling wave taken at t=0.3s. The wavelength is 7.5 cm and amplitude is 2 cm. if the crest P was at x=0 at t=0, write the equation of travelling wave.
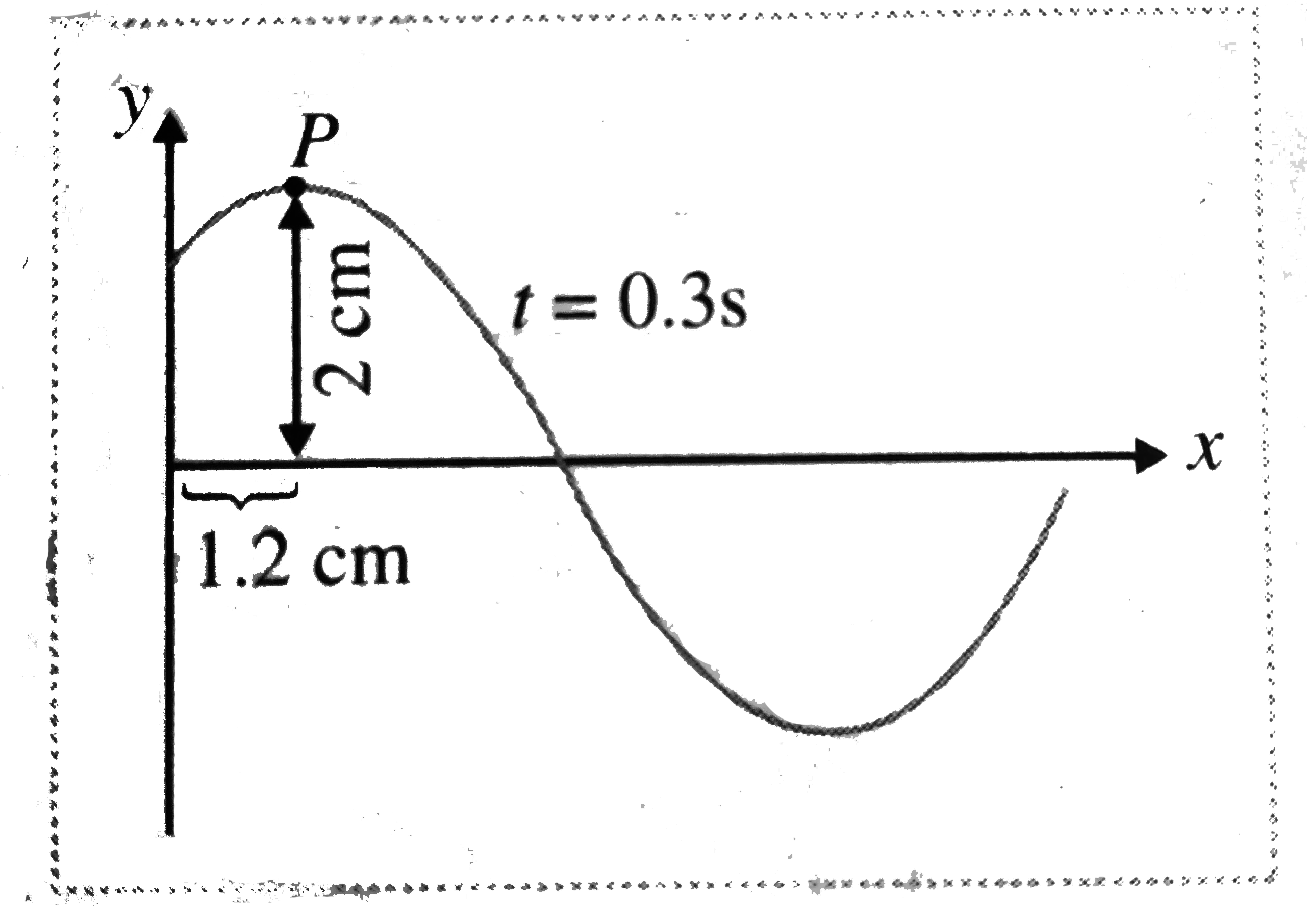 View Solution
View SolutionThe wave described by y =0.25sin(10πx−2πnt) where x and y are in meters and t in seconds , is a wave travelling along the
View SolutionThe equation of a transverse wave travelling on a rope given by y=10sinπ(0.01x−2.00t) whrer y and x are in cm and t in second .This maximum traverse speed of a particle in the rope is about
View Solution

