A sinusoidal wave trsvelling in the positive direction on a stretched string has amplitude , wavelength and velocity . At and it is given that and . Find the wave function .
The correct Answer is:A, B, D
We start with a general equation for a rightward moving wave,
The ampitude given is
A wavelength is given as
:. Angular wave number,
Angular frequency,
We are given that for , ,
and
i.e. (as )
and
From these conditions, we conclude that
, where ......
Therefore,
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Exercise 17.1
4 Videos
- WAVE MOTIONBOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Exercise 17.2
2 Videos
- WAVE MOTIONBOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Example Type 5
1 Videos
- VECTORSBOOK - DC PANDEYCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
A sinusoidal wave travelling in the positive x direction has an amplitude of 15 cm, wavelength 40 cm and frequency 8 Hz. The vertical displacement of the medium at t =0 and x = 0 is also 15 cm, as shown
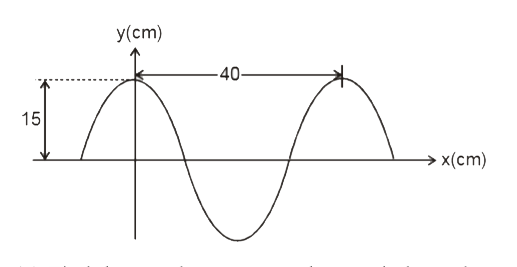
(a) Find the angular wave number, period angular frquency and speed of the wave.
View SolutionA sinusoidal wave travelling in the positive x direction has an amplitude of 15 cm, wavelength 40 cm and frequency 8 Hz. The vertical displacement of the medium at t =0 and x = 0 is also 15 cm, as shown
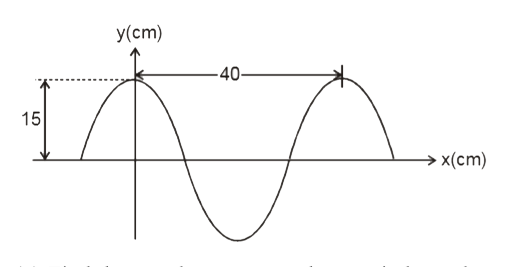
(b) Determine the phase constant ϕ, and write a general expression for the wave function.
View Solution
Knowledge Check
A progressive wave is travelling along the positive direction of the x-axis. For this wave, amplitude = 5 cm, period = 0.2 s and wavelength = 30 cm
The equation of the wave using SI units is given byAy=0.05sin2π(t0.2−x0.3)By=0.5sin2π(t0.2−x30)Cy=5sin2π(t0.2+x3)Dy=0.05sin2π(x0.3+t0.2)A transverse sinusoidal wave moves along a string in the positive x-direction at a speed of 10cm/s. The wavelength of ythe wave is 0.5m and its amplitude is 10cm. At a particular time t, the snap-shot of the wave is shown in figure. The velocity of point P when its displacement is 5cm is -
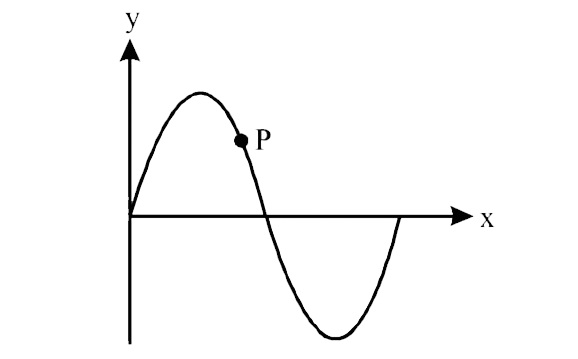 A(a) √350ˆJm/sB(b) −√350ˆJm/sC( c ) √350ˆim/sD(d) −√350ˆim/s
A(a) √350ˆJm/sB(b) −√350ˆJm/sC( c ) √350ˆim/sD(d) −√350ˆim/sA sinusoidal wave is propagating in negative x-direction in a string stretched along x-axis. A particle of string at x=2 cm is found at its mean position and it is moving in positive y-direction at t=1 s. the amplitude of the wave, the wavelength and the angular frequency of the wave are 0.1m,π/4m and 4πrad/s, respectively.
The instantaneous power transfer through x=2m and t=1.125s isA10J/sB4π/3J/sC2π/3J/sD0
A sinusoidal wave travelling in the positive x-direction has an amplitude of 15.0cm, a wavelength of 40.0cm and a frequency of 8.00Hz.Thevertic≤displacementofthemediumatt = 0 and x = 0isalso15.0 cmasshown∈figure.<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/DCP_V03_C17_E01_054_Q01.pngwh=80%mx-autosty≤=background:white;><br>(a)F∈dtheanga––rwaveνmberk,periodT,anga––requencyomegaandspeedv of the wave.
(b) Write a general expression for wave function.
View Solution(i) A sinusoidal wave is travelling along positive x direction and the displacements at two positions x=0 and x=1m are given by y(0,t)=0.2cos(3πt) and y(1,t)=0.2cos(3πt+π8) Find all possible wavelength of the wave if it is known that wavelength is greater than 0.4 m.
(ii) A transverse sine wave of amplitude a=0.1cm is travelling along a string laid along the x-axis. The displacement (y) – time (t) graph of the string particle at x=0.1m is shown in first figure. The shape of the string at time t=0.1s is shown in second figure. At this time the particle at x=0.11m is having velocity in positive y direction write the equation of wave.

View Solution(a) writ the expression for y as a function of x and t for a sinusoidal wave travelling along a rope in the neagative x direction with the folllowing characteristics: A =8.00 cm , δ=80.0cm,f=3.00Hz, and y(0,t)=0att=0, (b) write an expression for y as a function of x and t for the wave in part (a) assuming that y(x,0)=0 at the point x=10.0 cm.
View SolutionA transverse sinusoidal wave moves along a string in the positive x-direction at a speed of 10 cm/s. The wavelength of the wave is 0.5 m and its ampli- tude is 10 cm. At a particular time t, the snap-shot of the wave is shown in figure. The velocity of point P when its displacement is 5 cm is Figure :
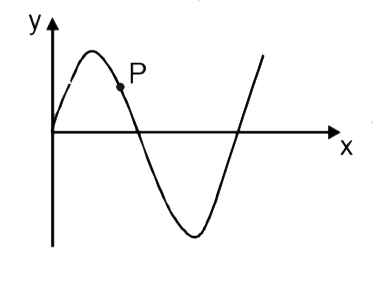
View SolutionA wave travels along the positive x-direction with a speed of 20ms−1. The amplitude of the wave is 0.20 cm and the wavelength 2.0 cm. (a) Write a suitable wave equation which describes this wave. (b) What is the displacement and velocity of the particle at x = 2.0 cm at time t = 0 according to the wave equation written ? Can you get different values of this quantity if the wave equation is written in a different fashion ?
View Solution
