The
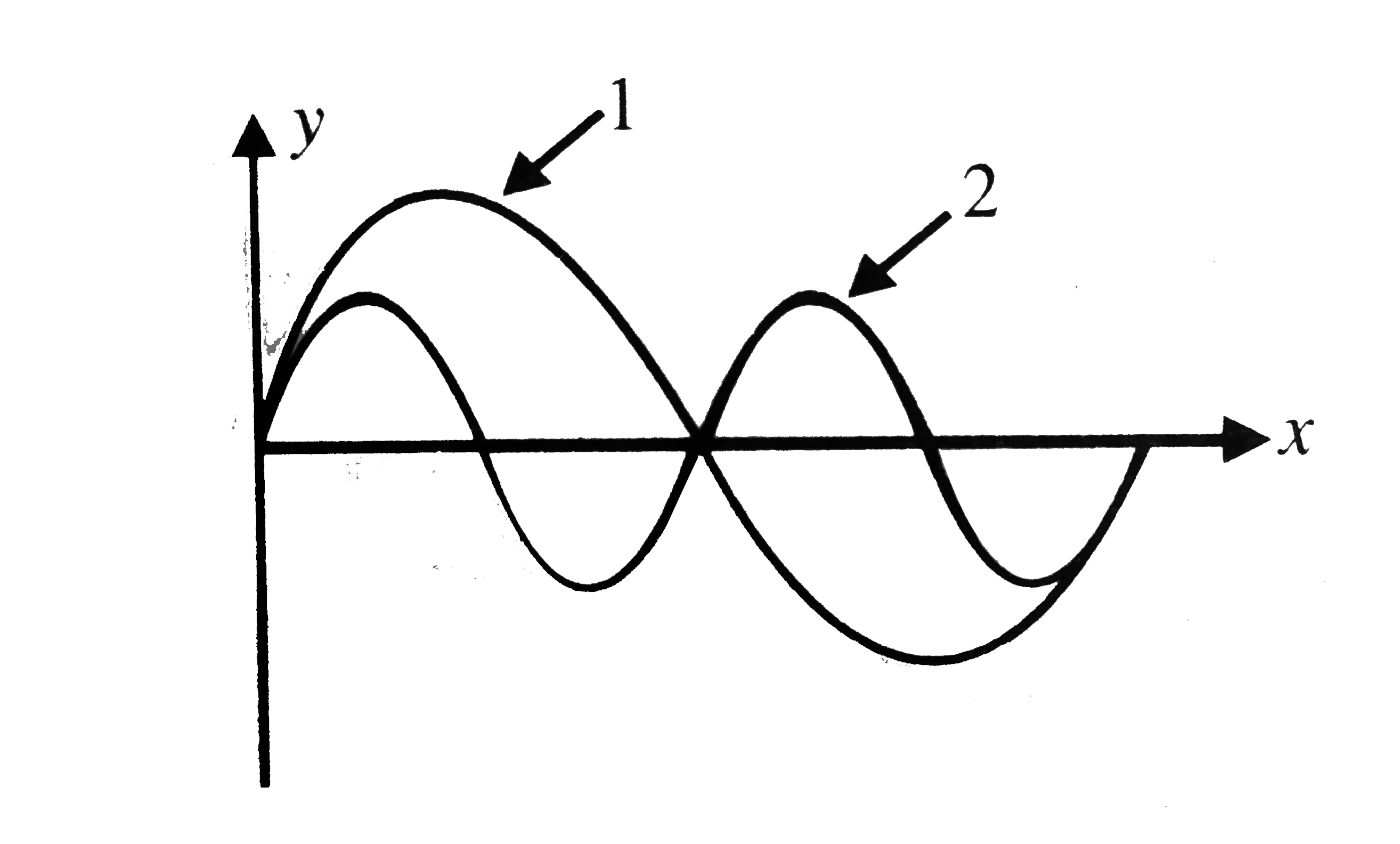
shows two snapshots, each of a wave travelling along a particular string. The phase for the waves are given by (a) 4x-8t (b) 8x-16t. Which phase corresponds to which waves in
The standard equation of a plane progressive wave is y=Asin(kx−ωt), the phase of the wave is (kx−ωt), we get ω=16andk=8
λ2=2πk=2π8=π4
clearly λ1=2λ2
Therefore, snapshots 1 and 2 correspond to a and b respectly.
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Subjective
16 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct
62 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.1
9 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICSCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
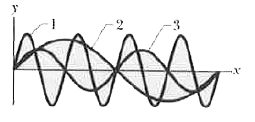
The figure is a composite of three snapshots, each of a wave traveling along a particular string. The phases for the waves are given by (a) 2x-4t, (b) 4x-8t, and (c) 8x-16t. Which phase corresponds to which wave in the figure.
View SolutionThe equation of a wave travelling on a string stretched along the X-axis is given by
y=Ae(−xa+tT)2
(a) Write the dimensions of A, a and T.
(b) Find the wave speed.
(c) In which direction is the wave travelling?
(d) Where is the maximum of the pulse located at t=T and at t=2T?
View Solution
Knowledge Check
Consider the snapshot of a wave traveling in positive x–direction
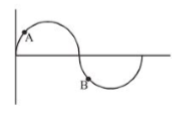 AThe particle A is moving in –ve y–direction and particle B is moving in +y–directionBThe particle B is moving in –ve y–direction and particle A is moving in +y–directionCBoth are moving in the +ve y–directionDBoth are moving in the –ve y–direction
AThe particle A is moving in –ve y–direction and particle B is moving in +y–directionBThe particle B is moving in –ve y–direction and particle A is moving in +y–directionCBoth are moving in the +ve y–directionDBoth are moving in the –ve y–directionA harmonic wave is travelling along +ve x-axis, on a stretched string. If wavelength of the wave gets doubled, then
Afrequency of wave may changeBwave speed may changeCboth frequency and speed of wave may changeDonly frequency will changeThe equation of a wave travelling on a stretched string along the x-axis is y=ae−(bx+ct). The direction of propagation of wave is
Aalong negative y-axisBalong positive y-axisCalong negative x-axisDalong positive x-axis
The equation of a wve travelling on a string stretched along the X-axis is given by
y=Ad−(xatT)2
a. Write the dimensions of A, a and T. b. Find the wave speed. c.In which direction is the wave travelling? d.Where is the maximum of the pulse located at t=T?Att=2T?
View SolutionThe equation of a wave travelling on a string is given by Y(mn) = 8 sin[(5m−1x−(4s−1t]. Then
View SolutionIn a string under tension T, the velocity of transverse wave travelling along it is
View SolutionThe equation of a transverse wave travelling along a string is given by y=5cosπ(100t−x)cm. Its wavelength is
View SolutionThe equation of a wave travelling on a stretched string is y = 4 sin 2π(t0.02−x100)
Here, x and y are in cm and t is in second. The speed of wave is
View Solution