A circular loop of string rotates about its axis on a frictionless horizontal plane at a uniform rate so that the tangential speed of any particle of the string is v. if a small transvers disturbance is produced at a point of the loop,with what speed (relative to the string) will this disturbance travel on the string?
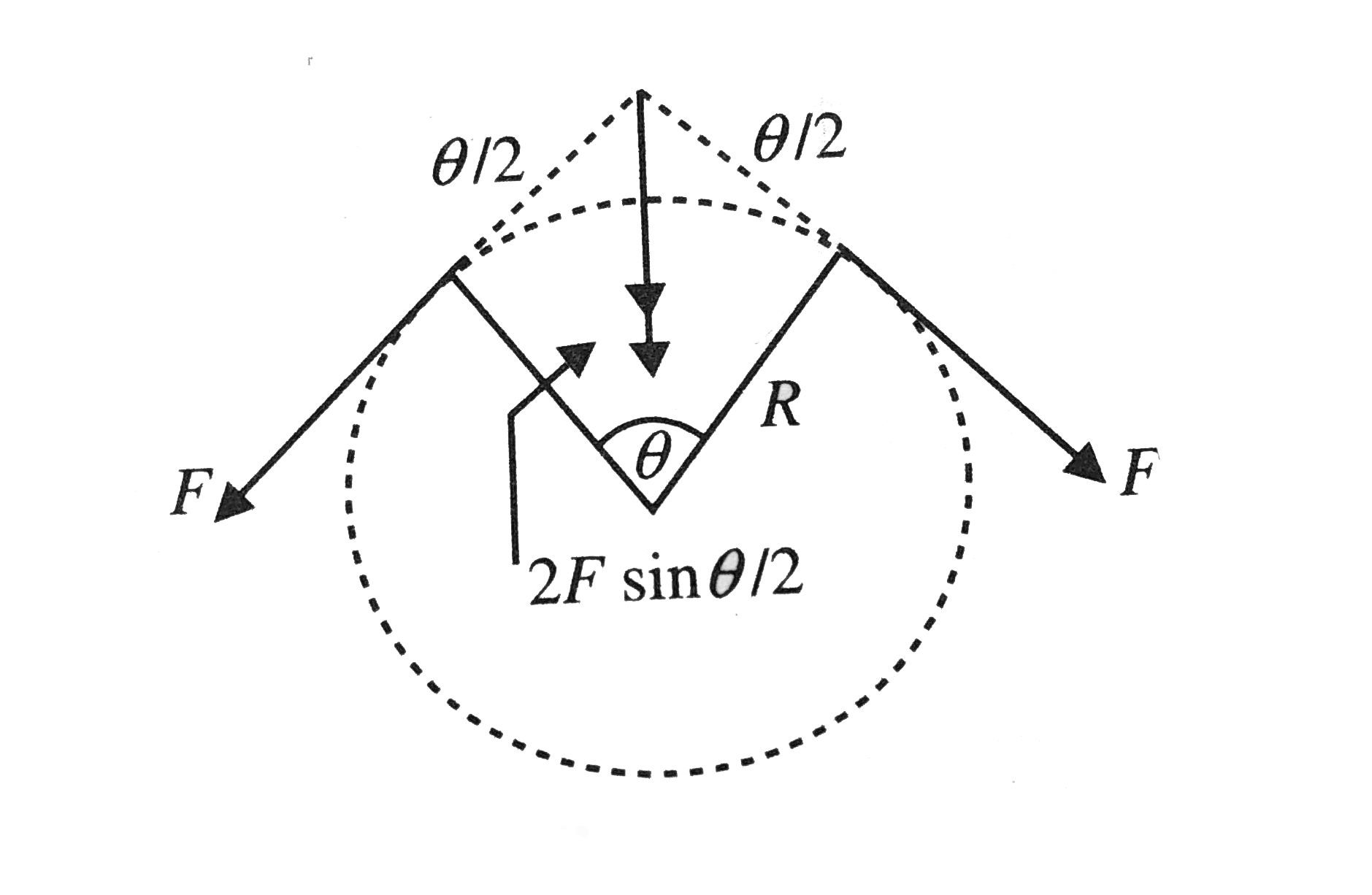
Suppose F is the tension in the string due to its rotation. Choose a small element of the string of length l. if is the mass per unit length of the string, then mass of the element, using newton's second law for the element, we have
For small
2F(theta/2)=(mv^(2))/(R)Ftheta=(muRtheta)V^(2)/RF=muv^(2)=sqrt(F)/(mu)=sqrt(muv^(2))/(mu)=v
Topper's Solved these Questions
- TRAVELLING WAVESBook:CENGAGE PHYSICSChapter:TRAVELLING WAVESExercise:Subjective
Explore 16 Videos
- TRAVELLING WAVESBook:CENGAGE PHYSICSChapter:TRAVELLING WAVESExercise:Single Correct
Explore 62 Videos
- TRAVELLING WAVESBook:CENGAGE PHYSICSChapter:TRAVELLING WAVESExercise:Exercise 5.1
Explore 9 Videos
- TRANSMISSION OF HEATBook:CENGAGE PHYSICSChapter:TRANSMISSION OF HEATExercise:Single correct
Explore 9 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
A circular loop of string rotates about its axis on a frictionless horizontal plane at a uniform rate so that the tangential speed of any particle of the string is u. If a small transverse disturbance is produced at a point of the loop, with what speed (relative to the string) will this disturbance travel on the string ?
View SolutionA uniform circular hoop of string is rotating clockwise in the absence of gravity. The tangential speed is v0. Find the speed of the wave travelling on this string.
View Solution
Knowledge Check
A string of mass M as a circular loop rotates abot its axis on a frictionless horizontal plane at a uniform rate so that the tangential plane at a uniform rate so that the tangential speed of any particle of the string is v. If a small transverse disturbance is produced at a point of the loop, then speed (relative to the string) of disturbance on the string is
Av√M2B√2vCvDv√2A loop of a string of mass per unit length μ and radius R is rotated about an axis passing through centre perpendicular to the plane with an angular velocityco. A small disturbance is created in the loop having the same sense of rotation. The linear speed of the disturbance for a stationary observer is :
AωRB2ωRC3ωRDZeroA stone tied to a string is rotated with a uniform speed in a vertical plane. If mass of the stone is m, the length of the string is r and linear speed of the stone is v when the stone is at its lowest point, then the tension in the string will be
(g= acceleration due to gravity)Amv2r+mgBmv2r−mgCmvrDmg
A uniform circular hoop of string is rotating clockwise in the absence of gravity. The tangential speed is v0. Find the speed of the wave travelling on this string.
View SolutionA loop of a string of mass length μ and redius R is rotated about an axis passing through centre perpendicular to the plane with an angular velocity ω.A small disturbance is created in the loop having the same sense of rotation. The linear speed of the disturbance observer is
View SolutionA string of length 2L, obeying Hooke's Law, is stretched so that its extension is L. The speed of the tranverse wave travelling on the string is v. if the string is futher stretched so that the extension in the string becomes 4L. The speed of transverse wave travelling on the string will be
View SolutionA string of length 2L, obeying hooke's law, is stretched so that its extension is L. the speed of the transverse wave travelling on the string is v. If the string is further stretched so that the extension in the string becomes 4L. The speed of transverse wave travelling on the string will be
View SolutionA loop of a string of mass length μ and redius R is rotated about an axis passing through centre perpendicular to the plane with an angular velocity ω.A small disturbance is created in the loop having the same sense of rotation. The linear speed of the disturbance observer is
View Solution
