A plane undamped harmonic wave progates in a medium. Find the mean space density of energy becomes equal to W0 at an instant t=t(0)+T/6, where t0 is the instant when amplitude is maximum at this location and T is the time period of oscillation.
Let us consider the wave
Y=Acos(ωt−kx),
then its energy density (energy per unit volume)is given by W=pA2ω2sin2(ωt−kx) [where p is of medium, for string waves, μ=pS].
Let us consider x=0, t0=0 at which amplitude is maximum
At t=t0+T6
And t=Acos[ωT6]
and the energy density is
w=pA2ω2sin2[ωT6]=pA2ω2sin2(π)3
W=(pA2ω2)34
From given data, W=W0
⇒pA2ω2=43W0=(2W03
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct
62 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct Answer
1 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.2
23 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICSCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A plane undamped harmonic wave propagates in a medium. Find the mean space density of the total oscillation energy (:w:), if at any point of the medium the space density of the total oscillation energy becomes equal to w0 one− sixth of an oscillation perio after passing the displacement maximum
View SolutionA harmonic wave travelling in a medium has a period T and wavelength X. How far does the wave travel in time T ?
View Solution
Knowledge Check
an object of mass 0.5 kg is executing simple harmonic motion. It amplitude is 5 cm and time period (T) is 0.2 s. What will be the potential energy of the object at an instant t=T4s starting from mean position. Assume that the initial phase of the oscillation is zero.
A0.62JB6.2×10−3JC1.2×103JD6.2×103JIn the given at t=0, switch S is closed.
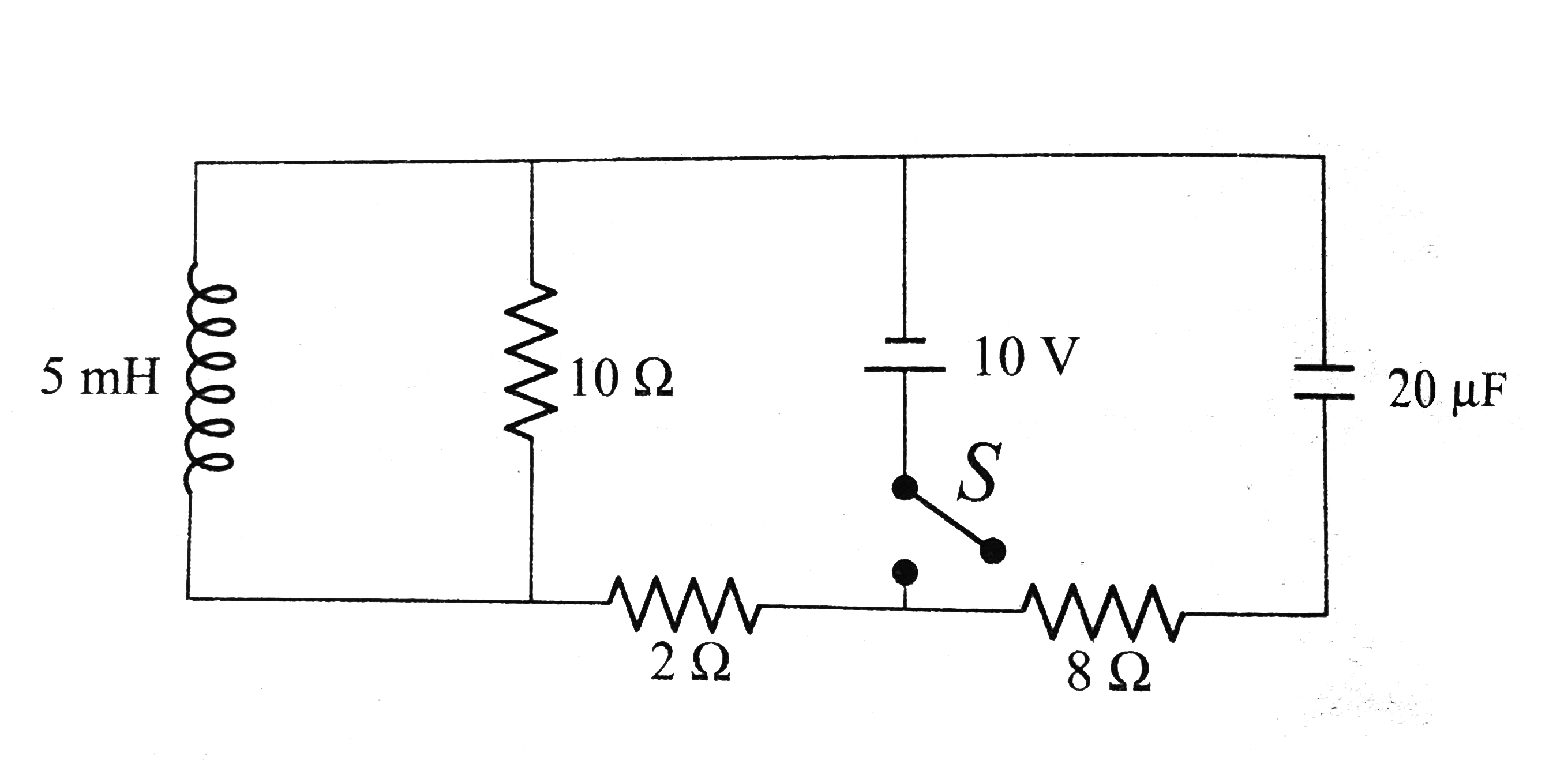
The energy stored in the inductor at any instant t(0<t∞) will beA12[5−5e−(1000/3)t]2mJB1252[1−e−(1000/3)t]2mJC252[1−e−(1000/3)t]2mJD52[1−e−(1000/3)t]2mJA particle starts simple harmonic motion from the mean position. If It's amplitude is A and time period T, then at a certain instant, its speed is half of its maximum speed at this instant, the displacement is
A√2A3B√3A2C2A√3D3A√2
In the given at t=0, switch S is closed.

The energy stored in the inductor at any instant t(0<t∞) will be
View SolutionA simple pendulum of length l0 can perform simple harmonic oscillations with a time period T0. If the length of the pendulum is decreased to l016 then the time time period of oscillation will become.
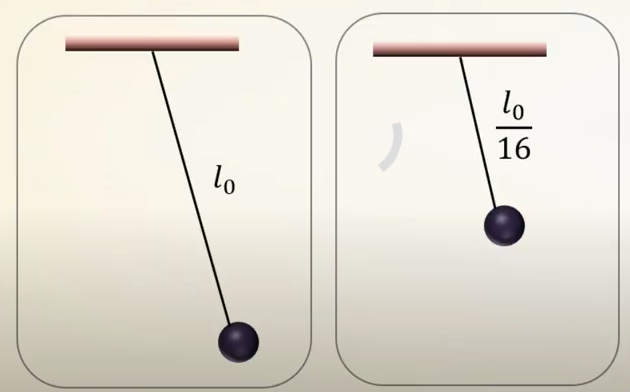
View SolutionA wave propagates in a string in the positive x-direction with velocity v. The shape of the string at t=t0 is given by
f(x,t0)=Asin(x2a2). Then the wave equation at any instant t is given by
View SolutionA body of mass m is moving along a circular path of radius R such that its kinetic energy at any instant is k=k0(tt0)2
where t0 is an appropriate constant. Then
View SolutionA wave propagates in a string in the positive x-direction with velocity v. The shape of the string at t=t0 is given by
f(x,t0)=Asin(x2a2). Then the wave equation at any instant t is given by
View Solution
