A wave propagates in a string in the positive x-direction with velocity v. The shape of the string at t=t0 is given by
f(x,t0)=Asin(x2a2). Then the wave equation at any instant t is given by
g(x,t)=Asin[x−v(t−t0)]2a2
g(x,t)=Asin[x+v(t−t0)]2a2
g(x,t)=Asin[x−v(t+t0)]2a2
g(x,t)=Asin[x+v(t+t0)]2a2
The correct Answer is:A
To derive the wave equation for the given scenario, we start with the provided information about the wave shape at a specific time t0.
1. Identify the Initial Wave Shape:
The shape of the string at time t=t0 is given by:
f(x,t0)=Asin(x2a2)
2. General Form of Wave Equation:
The general equation for a wave propagating in the positive x-direction is:
g(x,t)=Asin(kx−ωt)
where k is the wave number and ω is the angular frequency.
3. Relate Wave Parameters:
We know that the wave speed v is related to the wavelength λ and the period T by:
v=λT
From this, we can express T as:
T=λv
4. Compare Given Wave Shape with General Form:
The given wave shape does not have a time-dependent term. To incorporate time, we consider the wave's propagation from t0 to a later time t. We can express the wave at time t as:
g(x,t)=Asin(x2a2−va(t−t0))
5. Substituting the Wave Parameters:
We can rewrite the wave equation using the relationship between k and a:
g(x,t)=Asin(x2a2−va(t−t0))
6. Final Wave Equation:
The final wave equation at any time t is:
g(x,t)=Asin(x−vt+vt0a)
This can be simplified to:
g(x,t)=Asin(x−vt+vt0a)
Final Result:
Thus, the wave equation at any instant t is:
g(x,t)=Asin(x−v(t−t0)a)
The shape of the string at time t=t0 is given by:
f(x,t0)=Asin(x2a2)
The general equation for a wave propagating in the positive x-direction is:
g(x,t)=Asin(kx−ωt)
where k is the wave number and ω is the angular frequency.
We know that the wave speed v is related to the wavelength λ and the period T by:
v=λT
From this, we can express T as:
T=λv
The given wave shape does not have a time-dependent term. To incorporate time, we consider the wave's propagation from t0 to a later time t. We can express the wave at time t as:
g(x,t)=Asin(x2a2−va(t−t0))
We can rewrite the wave equation using the relationship between k and a:
g(x,t)=Asin(x2a2−va(t−t0))
The final wave equation at any time t is:
g(x,t)=Asin(x−vt+vt0a)
This can be simplified to:
g(x,t)=Asin(x−vt+vt0a)
Thus, the wave equation at any instant t is:
g(x,t)=Asin(x−v(t−t0)a)
Similar Questions
A wave pulse is travelling on a string with a speed v towards the positive X-axis. The shape of the string at t = 0 is given by g(x)=Asin(xa), where A and a are constants. (a) What are the dimensions of A and a ? (b) Write the equation of the wave for a general time 1, if the wave speed is v.
View SolutionA pulse is propagating on a long stretched string along its length taken as positive x-axis. Shape of the string at t = 0 is given by y=√a2−x2when |x|≤a=0 when |x|≥a . What is the general equation of pulse after some time 't' , if it is travelling along positive x-direction with speed V?
View Solution
Knowledge Check
A wave is represented by the equation
y=Asin(10πx+15πt+π/3)
Where x is in metre and t is in second.
a wave travelling in the positive x-direction with a velocity of 1.5 m/s
a wave travelling in the negative x-direction with a velocity 1.5 m/s
a wave travelling in the negative x-direction with a wavelength of 0.2 m
a wave travelling in the positive x-direction with a wavelength 0.2 mAa wave travelling in the positive x-direction with a velocity of 1.5 m/sBa wave travelling in the negative x-direction with a velocity 1.5 m/sCa wave travelling in the negative x-direction with a wavelength of 0.2 mDa wave travelling in the positive x-direction with a wavelength 0.2 m
A wave is propagating along x-axis. The displacement of particles of the medium in z-direction at t=0 is given by : z=exp[−(x+2)2] where 'x' is in meter. At t=1s, the same wave disturbance is given by z=exp[−(x−2)2]. Then the wave propagation velocity is :-
View SolutionFor a wave propagating in the positive x direction the instantaneous displacement of the particle is y=Asin2πT(t−xv). What is the significance of the negative sign ? If positive sign is used, what does it represent?
View SolutionA progressive wave travelling along the positive x-direction is represented by y(x,t)=Asin(kx−ωt+ϕ). Its snapshot at t=0 is given in the figure.
For this wave, the phase is:
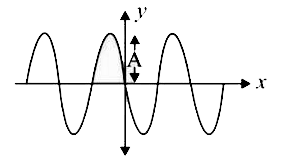
View SolutionA progressive wave travelling along the positive x-direction is represented by y(x,t)=Asin(kx−ωt+ϕ). Its snapshot at t=0 is given in the figure.
For this wave, the phase is:

View SolutionThe equation of a wave travelling on a string is given by Y(mn) = 8 sin[(5m−1x−(4s−1t]. Then
View SolutionConsider a wave sent down a string in the positive direction whose equation is given is
y=y0sin[ω(t−xv)]
The wave is propagated along because each string segment pulls upward and downward on the segment adjacent to it a slightly larger value of x and, as a result does work upon the string segment to which wave is travelling.
For example, the portion of string at point A is going upward, and will pull the portion at point B upward as well. In fact, at any point along the string, each segment of the string is pulling on the segment just adjacent and to its right, causing the wagve to propagate. It is by this process that the energy is sent along the string.
Now we try to calculate how much energy is propagated down the stirng per second
Ty=tsinθ≈Ttanθ⇒Ty=−T∂y∂x
(The negative sign appears because as shown in the figure II, the slope is negative) the force will act through a distance
dy=vydt=∂y∂tdt
Therefore work done by force in time dt is
dW=Tydy=−T(∂y∂x)(∂y∂t)dt⇒dW=ω2y20Tvcos2[ω(t−xV)]dt.....(A)
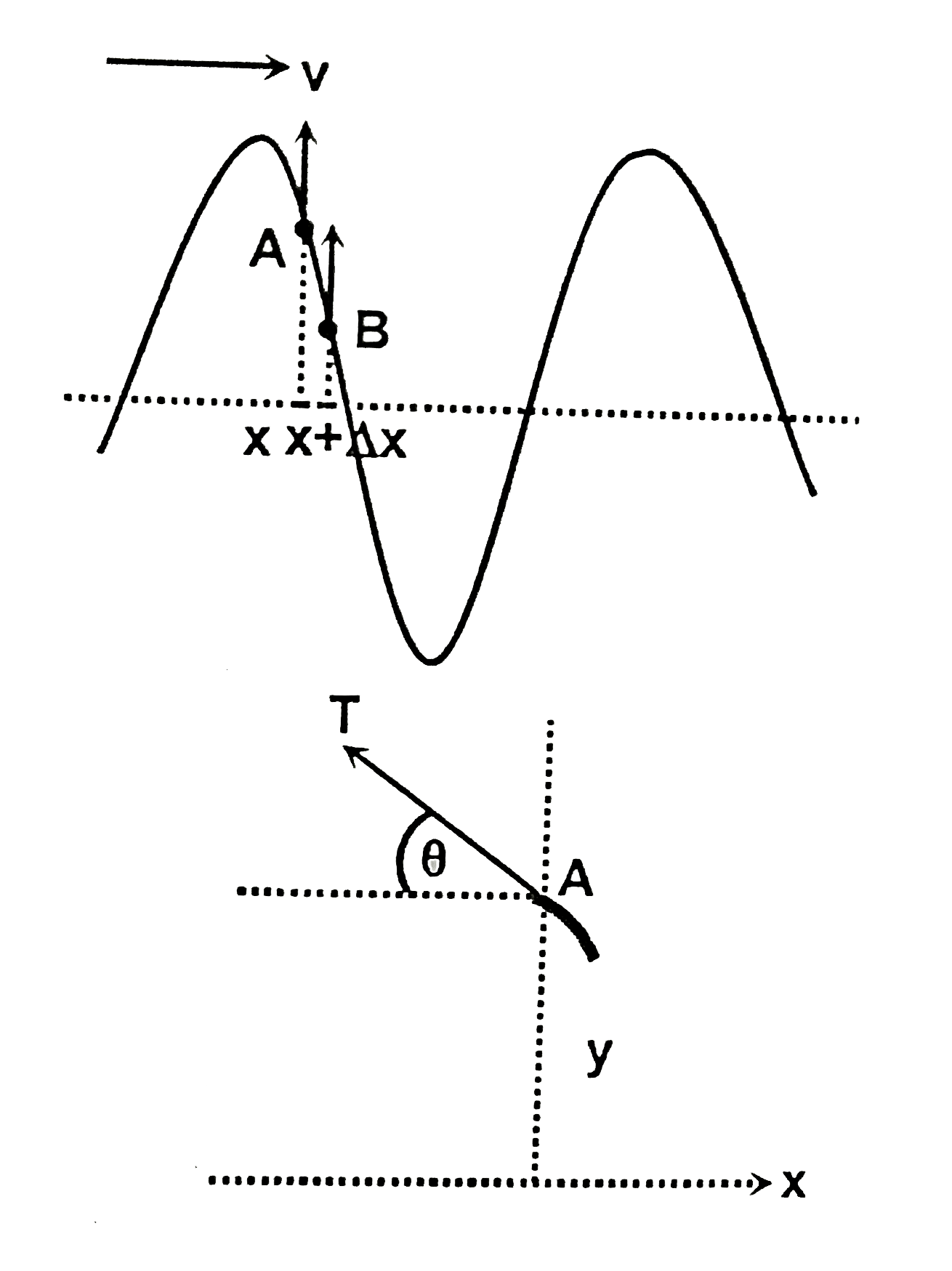
The average power transmitted down the string (i.e. the average energy transfer or sent down it per second) is
View SolutionThe displacement of the particle at x = 0 of a stretched string carrying a wave in the positive x-direction is given by f(t)=Asin(tT). The wave speed is v. Write the wave equation.
View Solution
