A water surfer is moving at a speed of 15m/s. When he is surfing in the direction of wave, he swing upwards every 0.8 s because of wave crests. While surfing in opposite direction to that of wave motion, he swings upwards every 0.6 s. determine the wavelength of transverse component of the water wave.
15 m
10.3 m
21.6 m
information insufficient
The correct Answer is:b
Let the speed of wave be v, for crossing one wave crests to the other while travelling in the same direction, the surfing speed has to be greater than speed of the wave, i.e., v<15m/s.
Let wavelength of wave be λ m
while surfing in the same direction,
λ=(15−v)×0.8
while surfing in the direction opposite to the wave motion,
λ=(15+v)×0.6
(15−v)0.8=(15+v)0.6
v=15/7m/s=2.143m/s
so, λ=(15−2.143)×0.8=10.3m
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct Answer1videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Multiple Correct25videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Subjective16videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct9videos
TRANSMISSION OF HEAT
- BOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
Transverse waves travel with a speed of 20.0m/sin a string under a tension of 6.00 N. what tension is requared for a wave speed of 30.0m/s in the same string?
View SolutionTwo sinusoidal waves travelling in opposite directions interfere to produce a standing wave described by the equation y=(1.5)msin(0.200x)cos(100t), where x is in metres and t is in seconds. Determine the wavelength, frequency and speed of the interfering waves.
View Solution
Knowledge Check
- Question 1 - Select One
Two sound waves each of frequency 500Hz are travelling along the same line in opposite direction . If the speed of sound in air is 350 m/s. find the distance between the consecutive antinodes of the resulting stationary wave.
A0.15mB0.25mC0.35mD0.45m - Question 2 - Select One
A wave travelling in positive x-direction with a=0.2 m/s. Velocity = 360 m/s. and λ = 60 m, then correct expression for the wave is
Ay=0.2sin[2π(6t+x60)]By=0.2sin[π(6t+x60)]Cy=0.2sin[2π(6t−x60)]Dy=0.2sin[π(6t−x60)] - Question 3 - Select One or More
One end of a taut string of length 3m along the x-axis is fixed at x=0. The speed of the waves in the string is 100ms−1. The other end of the string is vibrating in the y-direction so that stationary waves are set up in the string. The possible wavelength(s) of these sationary waves is (are)
A(a) y(t)=Asin(πx)6cos(50πt)3B(b) y(t)=Asin(πx)3cos(100πt)3C( c ) y(t)=Asin(5πx)6cos(250πt)3D(d) y(t)=Asin(5πx)2cos250πt
Two sinusoidal waves travelling in opposite directions interfere to produce a standing wave described by the equation
y=(1.5m)sin(0.400x)cos(200t)
where, x is in meters and t is in seconds. Determine the wavelength, frequency and speed of the interfering waves.View SolutionA sinusoidal wave is propagating along a streched string that lies along the x-axis. The displacement of the string as a function of time is graphed in for particles at x-0 and at x=0.0900 m. (a) what is the amplitude of the wave? (b)what is the period of the wave? (c ) you are told that the two points x=0 and x=0.0900 m are within one wavelength of each other. if the wave is moving in the +x-direction, determine the wavelength and the wave speed. (d) if instead the wave is moving in the -x-direction, determine the wavelength and the wave speed. (e) would it be possible to derermine definitely the wavelength in parts (c ) and (d) if you were not told that the two points were within one wavelength of each other? why ot why not?
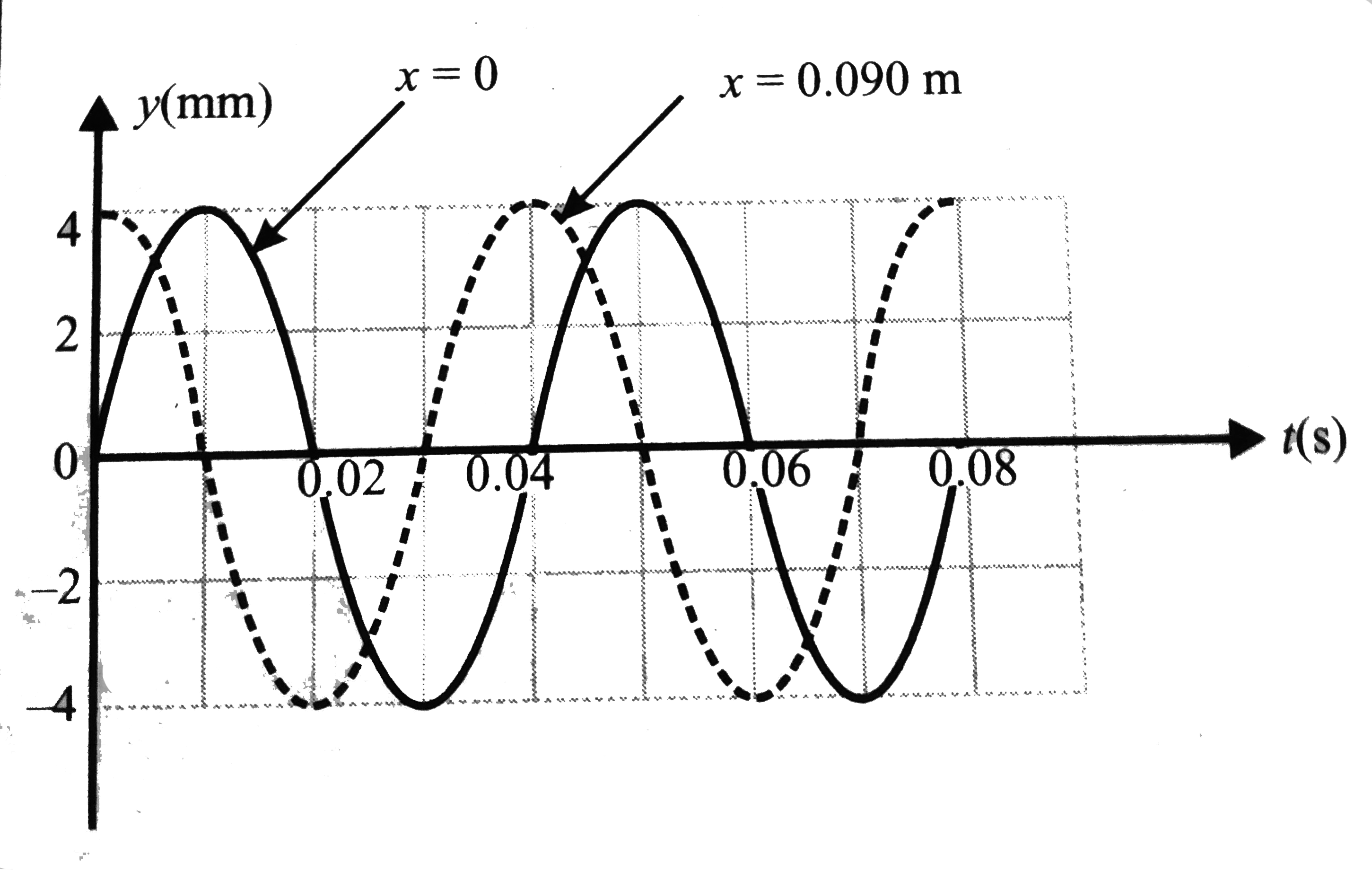 View Solution
View SolutionTwo sinusoidal waves with identical wavelengths and amplitudes travel in opposite directions along a string with a speed of 15 cm/s. If the time interval between instants when the string is fiat is 0.20 s, what is the wavelength of the waves?
View SolutionTransverse waves on a srting have speed 12.0m/s, amplitude 0.05m and wavelength 0.4m. The waves travel in the +x−direction and at t=0 the x=0 end of the string has zero displacement and is moving upwards.
(a) Write a wave function describing the wave.
(b) Find the transverse displacement of a point at x=0.25m at time t=0.15s.
( c ) How much time must elapse from the instant in part (b) until the point at x=0.25m has zero dispacement?View SolutionThe amplitude of a wave produced in a string is 5 cm. The wave is moving along positive direction of X-axis with a speed of 150 m/s and 5 vibrations are completed in 3 m length of the string. The equation representing the wave will be
View Solution

