The mathmaticaly form of three travelling waves are given by
$Y_{1} = (2 c m) sin (3 x - 6 t)$
$Y_{2} = (3 c m) sin (4 x - 12 t)$
And $Y_{3} = 94 c m) sin (5 x - 11 t)$
of these waves,

Wave 1 has greatest wave speed and greatest maximum transverse string speed

wave 2 has greatest wave speed and wave 1 has greatest maximum transverse string speed

wave 3 has greatest wave speed and wave 1 has greatest maximum transverse string speed

wave 2 has greatest wave speed and wave 3 has greatest maximum transverse string speed

Video Solution

Text Solution

Verified by Experts

The correct Answer is:d

Updated on:21/07/2023

Three traveling sinusoidal waves are on identical strings. with the same tension. The mathematical forms of the waves are $y_{1} (x, t) = y_{m} sin (3 x - 6 t), y_{2} (x, t) = y_{m} sin (4 x - 8 t), and y_{3} (x, t) sin (6 x - 12 t),$ where x is in meters and t is in seconds. Match each mathematical form to the appropriate graph below:
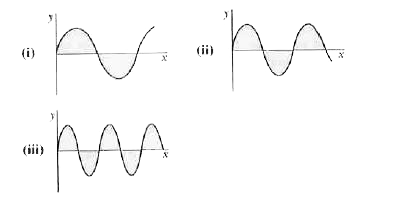A $y_{1} - (i), y_{2} - i i, y_{3} - (i i i)$
B $y_{1} - (i i i), y_{2} - (i i), y_{3} - (i)$
C $y_{1} - (i), y_{2} - (i i i), y_{3} - (i i)$
D $y_{1} - (i i), y_{2} - (i), y_{3} - (i i i)$
Two progressive transverse waves are described by :
$y_{1} = 3.0 c m sin [(4 x - 700 t) r a d]$ and
$y_{2} = 3.0 c m sin [(4 x - 700 t - π / 3) r a d]$ .
AAmplitude of a resultant wave is $3 \sqrt{3} c m$
BResultantis a standing wave.
CResultant is a progressive wave
DThe particle will be oscillating in xy-plane.
The displacement of a particle of a string carrying a travelling wave is given by $y = (4 c m) sin 2 π (0.5 x - 100 t)$ , where x is in cm and t is in seconds. The speed of the wave is
A50 cm/s
B100 cm/s
C200 cm/s
D250 cm/s