The figure shows a snap photograph of a vibrating string at . The particle is observed moving up with velocity . The tangent at makes an angle with x-axis.
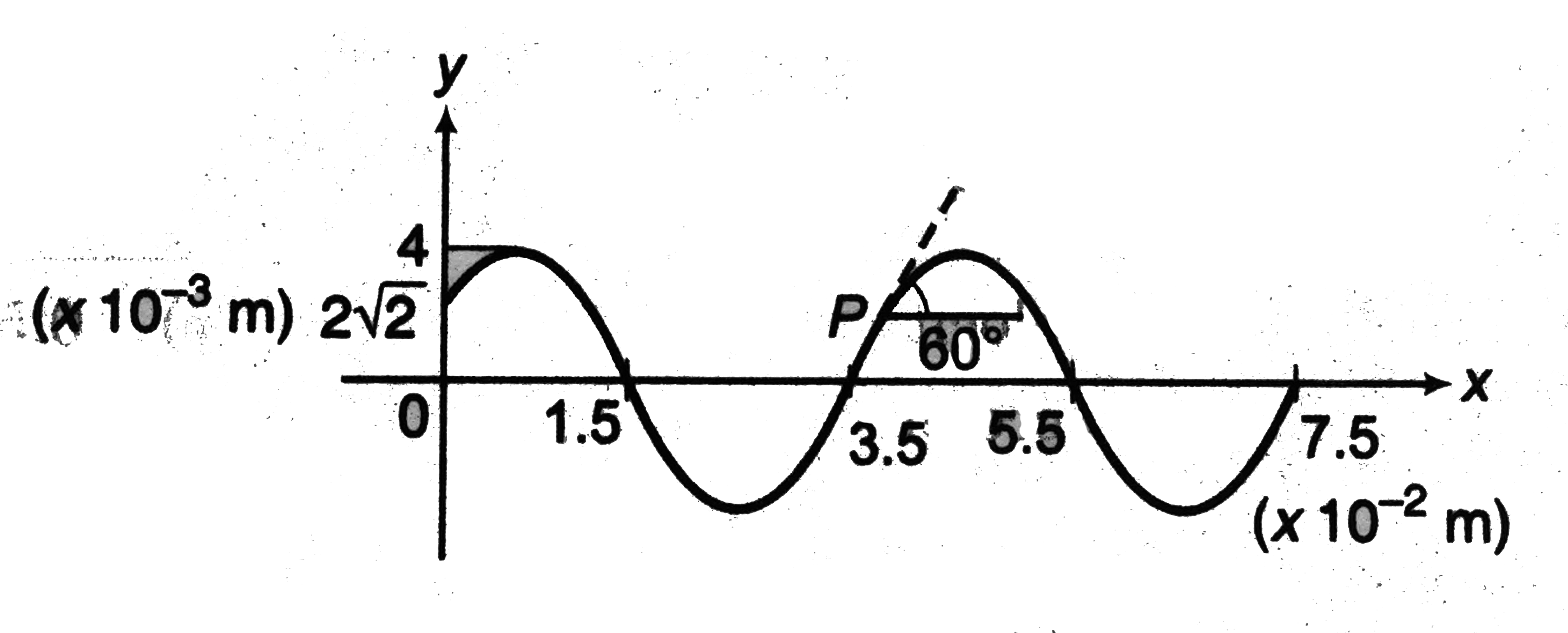
(a) Find the direction in which the wave is moving.
(b) Write the equation of the wave.
(c) The total energy carries by the wave per cycle of the string. Assuming that the mass per unit length of the string is .
The correct Answer is:d
(a). At slope of tangent
particle velocity
Hence, the wave is travelling in negative -direction with velocity .
(b). Frome graph, amplitude
wave length
wave number
Angular frequency
Hence, equation can be written as
at
particle is moving up at
Hence,
Hence, equation is
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Integer9videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Assertion-Reasoning6videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct9videos
TRANSMISSION OF HEAT
- BOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
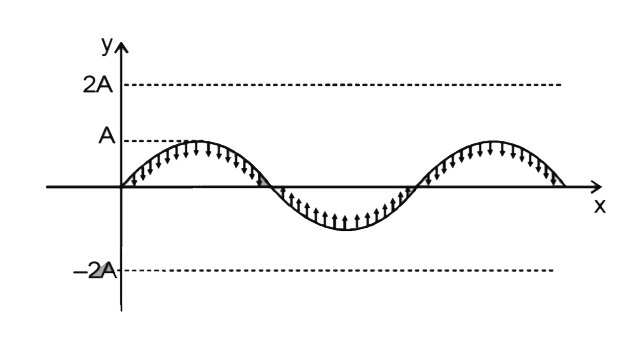
Figure shows the standing waves pattern in a string at t = 0. Find out the equation of the standing wave where the amplitude of antinode is 2A.
 View Solution
View SolutionFigure shows a plot of the transverse displacements of the particles of a string at t = 0 through which a travelling wave is passing in the positive x-direction. The wave speed is 20cms−1. Find (a) the amplitude, (b) the wavelength, (c) the wave number and (d) the frequency of the wave.
 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One
Waves formed on a string, such that energy is not carried by it. These waves are
Atransverse progressive wavesBlongitudinal progresive wavesCstationary wavesDelectromagnetic waves - Question 2 - Select One
A string fixed at both the ends forms standing waves with node separation of 5 cm. If the velocity of waves travelling in the string is 4 m/s, then the frequency of vibration of the string will be
A20 HzB30 HzC40 HzD50 Hz - Question 3 - Select One
The velocity of waves in a string fixed at both ends is 3 m/s. The string forms standing waves with nodes 6 cm apart. The frequency of vibration of the string is
A25 HzB50 HzC15 HzD10 Hz
Figure shows a plot of the transverse displacement of the particle of a string at t=0 through which a travelling wave is passing in the positive in the positive x-direction. The wave speed is 20cm/s. Find (a) the amplitude (b) the wavelength (c) the wave number and (d) the frequency of the wave.
 View Solution
View Solutionshows the position of a medium particle at t=0, supporting a simple harmonic wave travelling either along or opposite to the positive x-axis.

(a) write down the equation of the curve. (b) find the angle θ made by the tangent at point P with the x-axis. (c ) If the particle at P has a velocity vpm/s, in the negative y-direction, as shown in figure, then determine the speed and direction of the wave. (d) find the frequency of the wave. (e) find the displacement equation of the particle at the origin as a function of time. (f) find the displacement equation of the wave.View SolutionA transverse wave travelling in a string produce maximum transverse velocity of 3m/s and maximum transverse acceleration 90m/s2 in a particle. If the velocity of wave in the string is 20m/s. Datermine the equation of the wave ?
View SolutionStanding wavs are produced in a stretched string of length 8 m. If the string vibrates in 4 loops and the wave velocity is 20 m/s, then the frequency of the string will be
View SolutionStationary waves are produced in a stretched string of length 120 c. if the string vibrats with 6 segment and if the frquency of vibration of the string is 20 Hz. Then the velocity of waves on the string is
View Solution

