If A=[klmn] and kn≠lm, show that A2−(k+n)A+(kn−lm)l=O. Hence, find A−1
We, have, A[klmn], then |A|=∣∣∣klmn∣∣∣
=kn−ml≠0
∴ A−1∃.
Now, A2=A.A=[klmn][(k,l)(m,n)=[k2+lmkl+lnmk+nmml+n2]
∴ A2−(k+n)A+(kn−lm)I
=[k2+lmkl+lnmk+nmml+n2]−[(k−n)[klmn]+(kn−lm)[1001]
=[k2+lmkl+lnmk+nmml+n2][k2+nkkl+nlkm+nmkn+n2]+[kn−lm00kn−lm]
[k2+lm−K2−nk+kn−lmkl+ln−kl−lnmk+nm−km−nmml+n2−kn−n2+kn−lm]
[0000]=O
AsA2−(k+n)A+(kn−lm)I=O
⇒ (kn−lm)I=(k+n)A−A2
⇒ (kn−lm)IA−1=(k+n)A−A2)A−1
⇒ (kn−lm)A−1=(k+n)AA−1−A(AA−1)
=(k+n)I−AI
=(k+n)I−A
=(k+n)[1001]−[klmn]
=[k+n00k+n]−[klmn]
⇒ (kn−lm)A−1=[n−1−mk]
Hence A−1=1(kn−lm)[n−1−mk]
Similar Questions
Knowledge Check
Factories:
(l+m)2−4lmA(l+m−2lm)(l+m+2lm)B(l+m)2C(l−m)2Dnone of these
Show that ⌊kn is divisible by (⌊n)k
View SolutionIf α,β are the roots of the equation x2−lm+m=0, then find the value of 1α2+1β2 in terms of l and m.
View SolutionIf the angular frequency of small oscillations of a thin uniform vertical rod of mass m and length l hinged at the point O (Fig.) is √nl, then find n. The force constant for each spring is K/2 and take K=2mgl. The springs are of negiligible mass. (g=10m/s2)
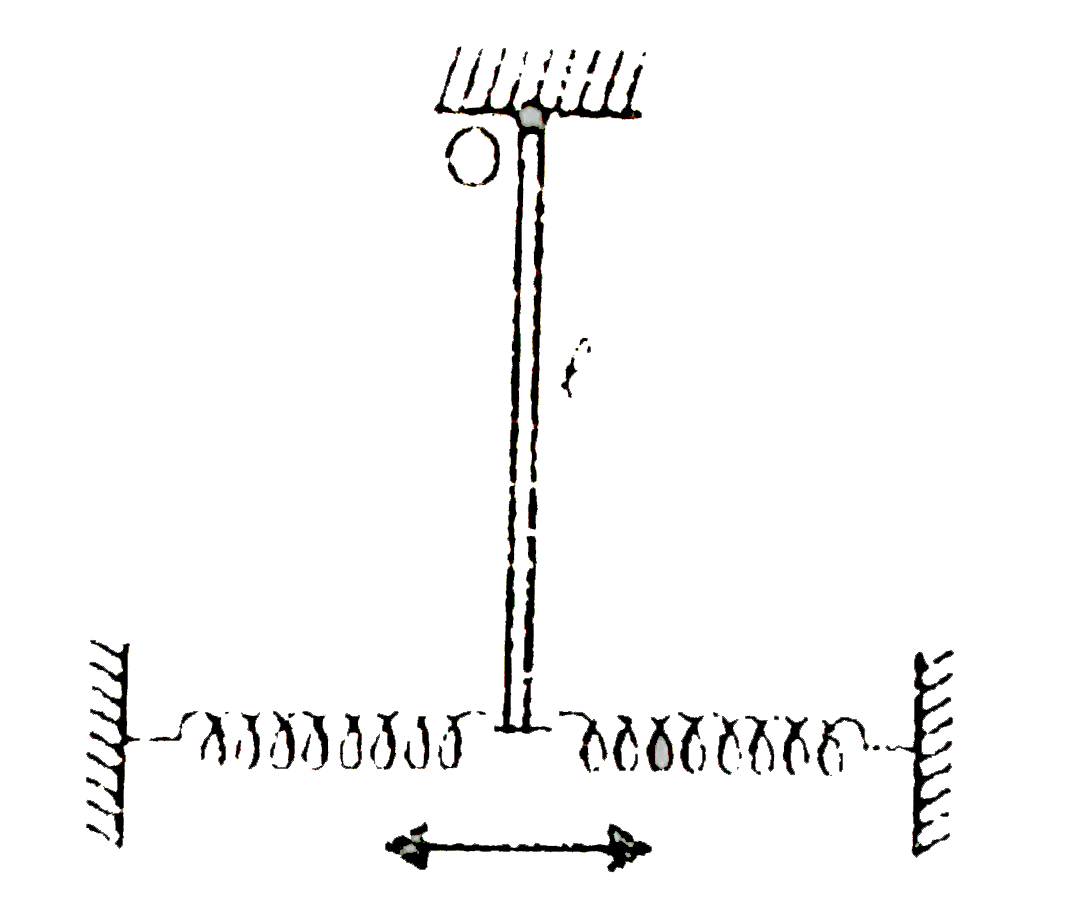
View SolutionIf the angular frequency of small oscillations of a thin uniform vertical rod of mass m and length l hinged at the point O (Fig.) is √nl, then find n. The force constant for each spring is K/2 and take K=2mgl. The springs are of negiligible mass. (g=10m/s2)
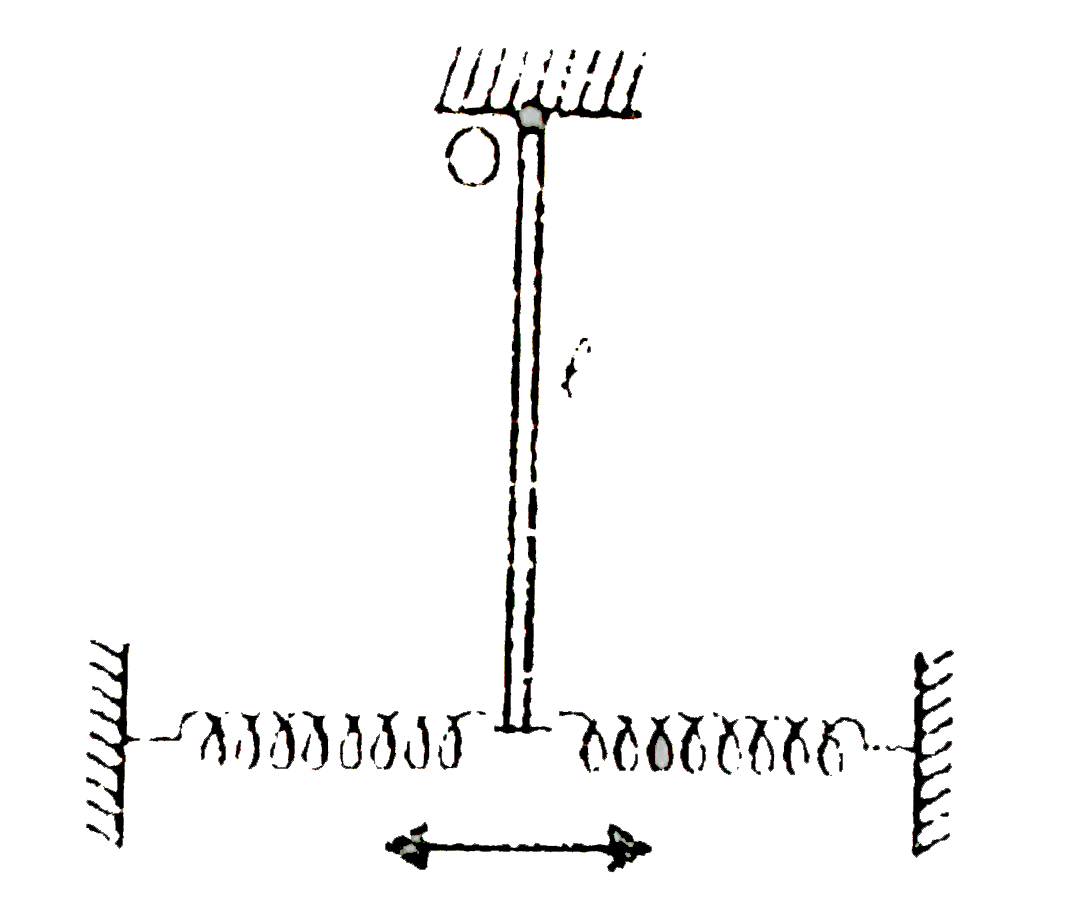
View SolutionIf I,mandn are real numbers such that l2+m2+n2=0 , then show that ⎡⎢⎣1+l2lmlnlm1+m2mnlnmn1+n2⎤⎥⎦=1
View SolutionFactoris the expression.
l2m2n−lm2n2−l2mn2
View SolutionIf KnLn=1024 where Kn=∫10xn(2−x)ndx,Ln=∫10xn(1−x)ndx, then n is equal to
View Solution
