If the angular frequency of small oscillations of a thin uniform vertical rod of mass m and length l hinged at the point O (Fig.) is √nl, then find n. The force constant for each spring is K/2 and take K=2mgl. The springs are of negiligible mass. (g=10m/s2)
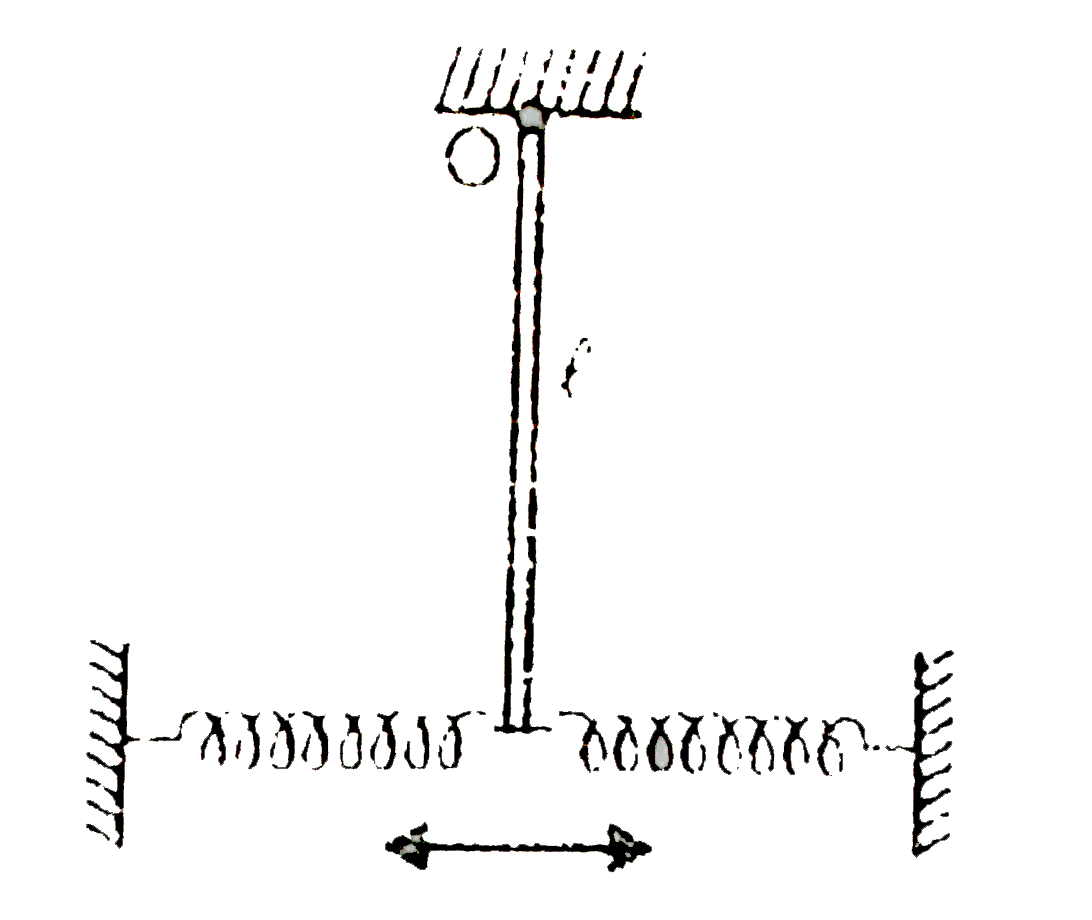
The correct Answer is:75
For small Angular displacement
Restoring torque about point O.
(mgl2sinθ)+(Klsinθ)l=ml23α, (for small θsinθ≈θ)
α=(mgl2+Kl2)θml23⇒α=[3g2l+3km]θ=−ω2θ
So angular speed ω=√3g2l+3kmθ=−ω2θ
ω=√3g2l(1+2klmg)=√75L∴N=75
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - II1videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - III12videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 1, PART - II37videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - SEMICONDUCTORSEXERCISE - Exercise 388videos
SEMICONDUCTORS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - FST-330videos
TEST PAPERS
Similar Questions
Find the frequency of small oscillations of thin uniform vertical rod of mass m and length l hinged at the point O.
 View Solution
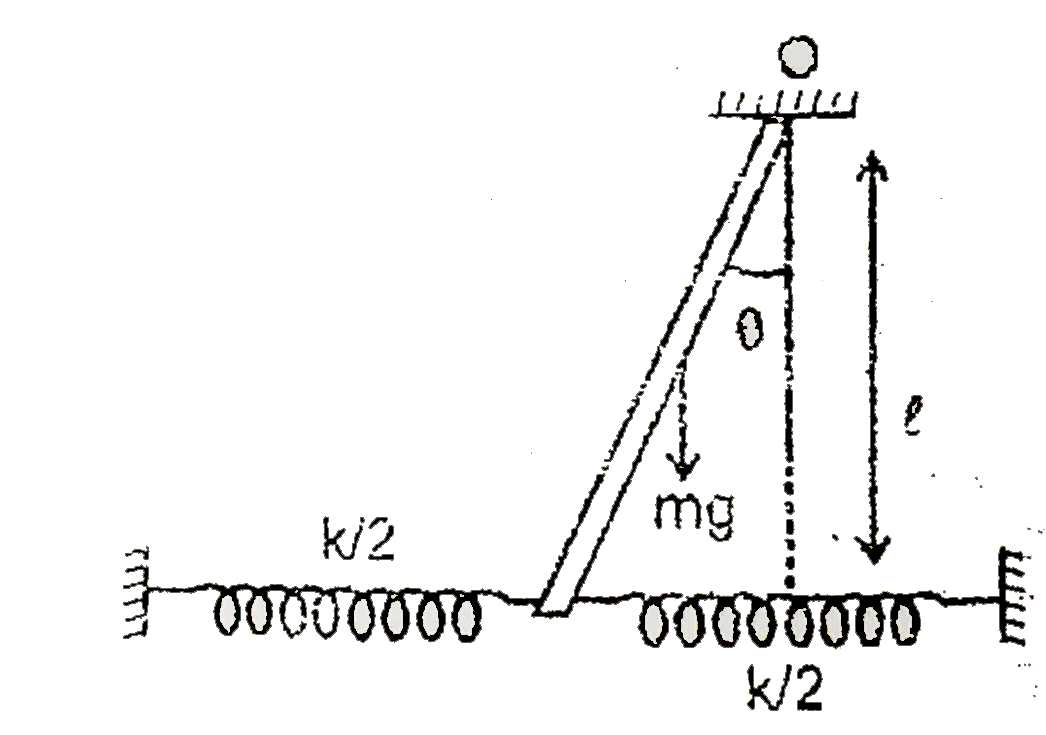
View SolutionFind the frequency of small oscillatinos of a thin uniform vertical rod of mass m and length l hinged at the point O (figure). The combined stiffness fo the springs is equal to x. The mass of the springs is negligible.
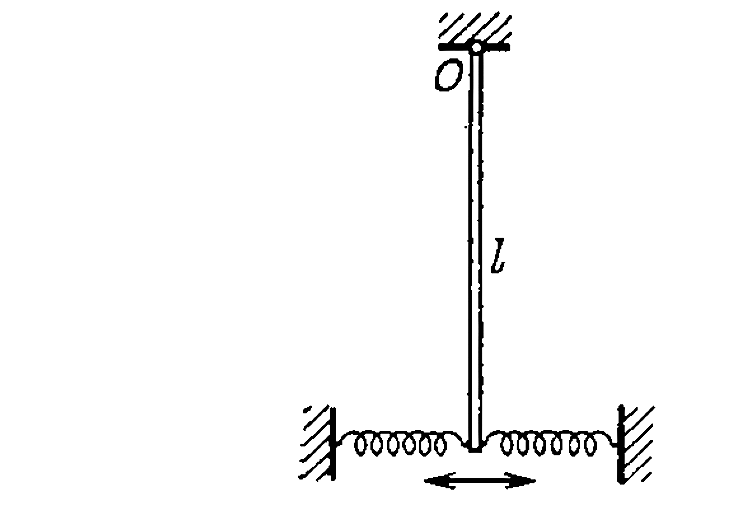 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A thin uniform vertical rod of mass m and length l pivoted at point O is shown in Fig. The combined stiffness of the springs is equal to k. The mass of the springs is negligible. The angular frequency of small oscillation is
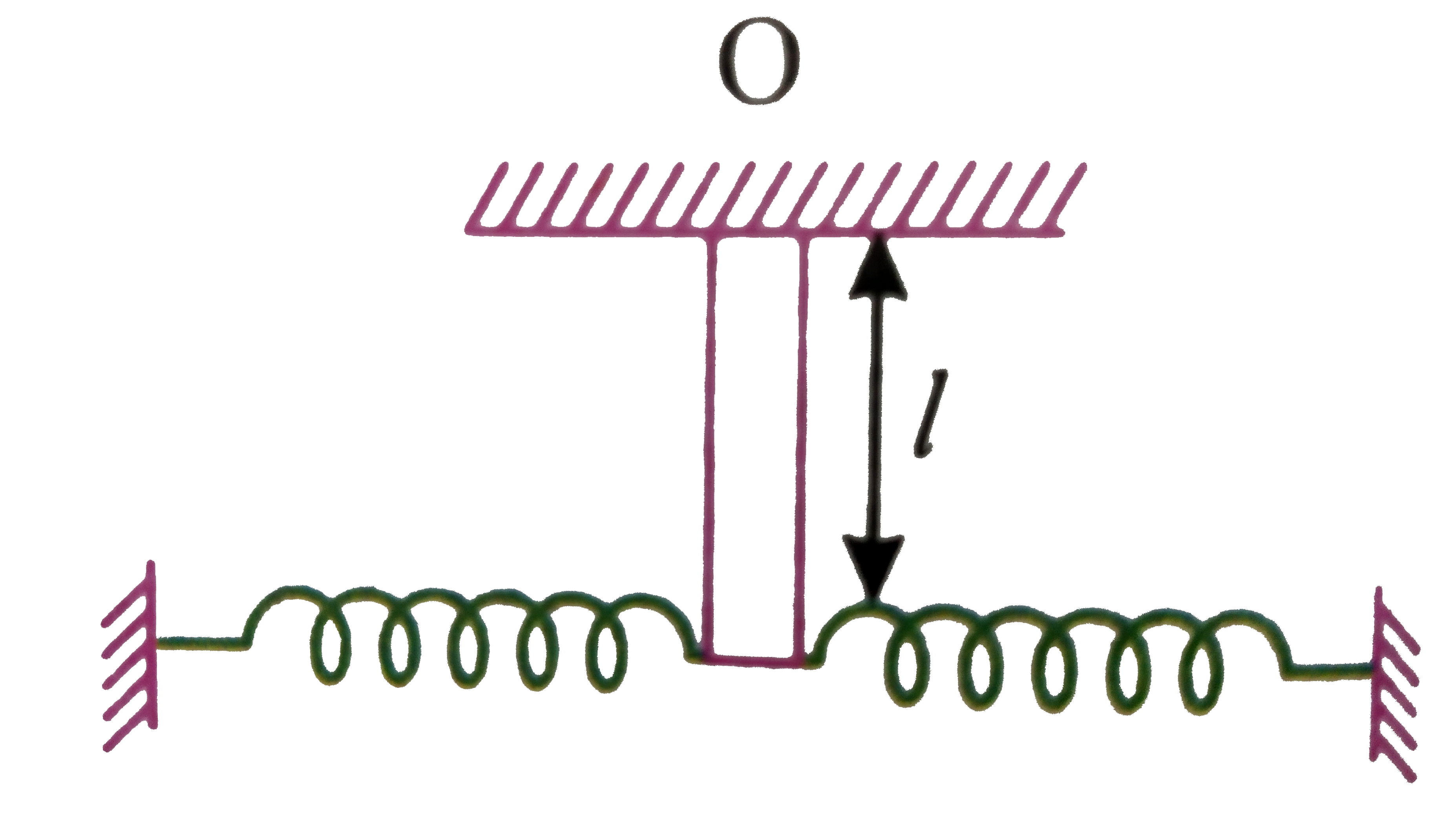 A√3k2m+glB√3k2m+3glC√3km+3g2lD√3km+2g3l
A√3k2m+glB√3k2m+3glC√3km+3g2lD√3km+2g3l - Question 2 - Select One

A thin uniform vertical rod of mass m and length l pivoted at point O is shown is Fig. The combined stiffness of the springs is equal to k. The mass of the spring is negligible. The frequency of small oscillation is .A√3k2m+glB√3k2m+3glC√3km+3g2lD√3km+2g3l - Question 3 - Select One
A uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
 A2π√lgB2π√2lgC2π√2l3gD2π√l3g
A2π√lgB2π√2lgC2π√2l3gD2π√l3g
Force constant of a spring is 100 N/m. If a 10kg block attached with the spring is at rest, then find extension in the spring.
(g=10m/s2)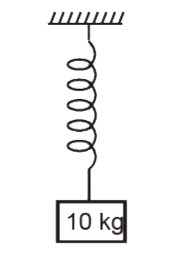 View Solution
View SolutionFind the period of small osciallations in a vertical plane performed by a small ball of mass m=50g fixed at the middle of a thin horizontal string of length l=1m and tensioned with a constant force T = 100N
View SolutionTwo springs are jonied and connected to a mass m as shown in figure. If the force constants of the two springs are k1andk2, shown that frequency of oscillation of mass m is
 View Solution
View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O
 View Solution
View SolutionTwo spring of force constants K and 2K are connected a mass m below The frequency of oscillation the mass is
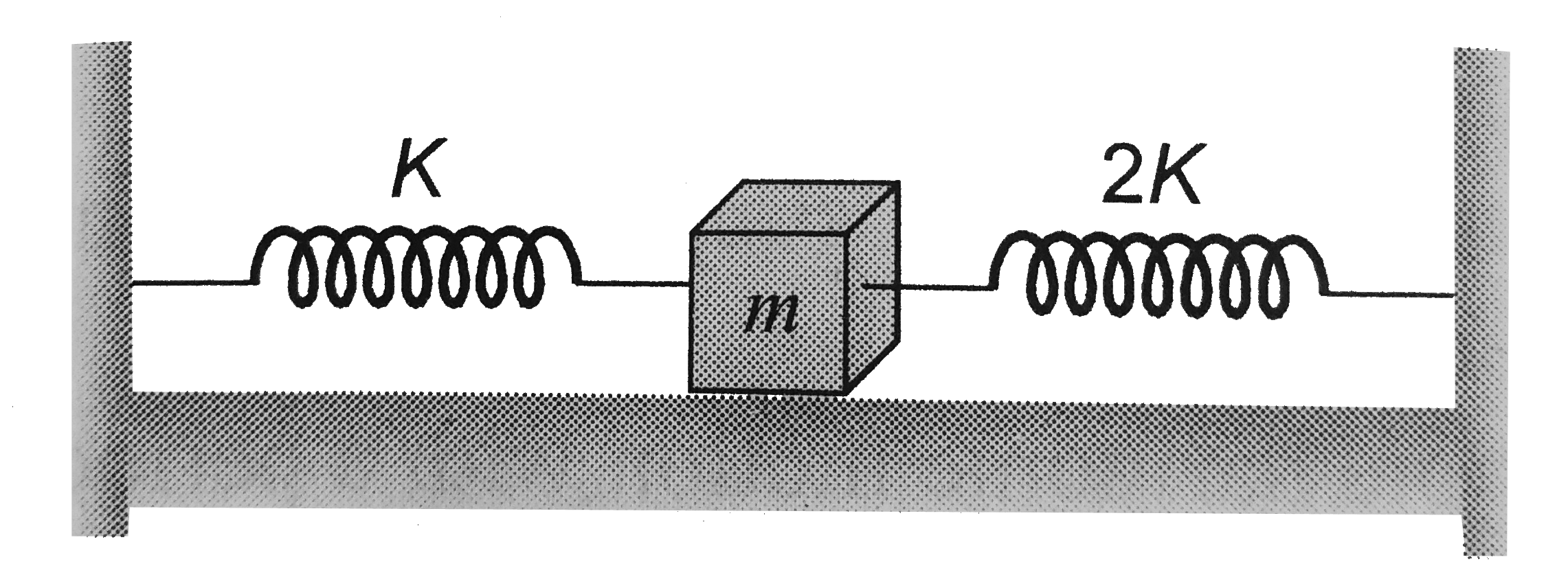 View Solution
View Solution

