a. Statement- 1 and Statement- 2 are true, and state-ment- 2 is the correct explanation of Statement- 1.
b. Statement- 1 and Statement- 2 are true but Statement- 2 is not the correct explanation of Statement- 1.
c. Statement- 1 is true and Statement- 2 is false.
d. Statement- 1 is false and Statement- 2 is true.
e. Statement- 1 is false and Statement- 2 is false.
Statement- 1:
Compound (I) is formed not (II).
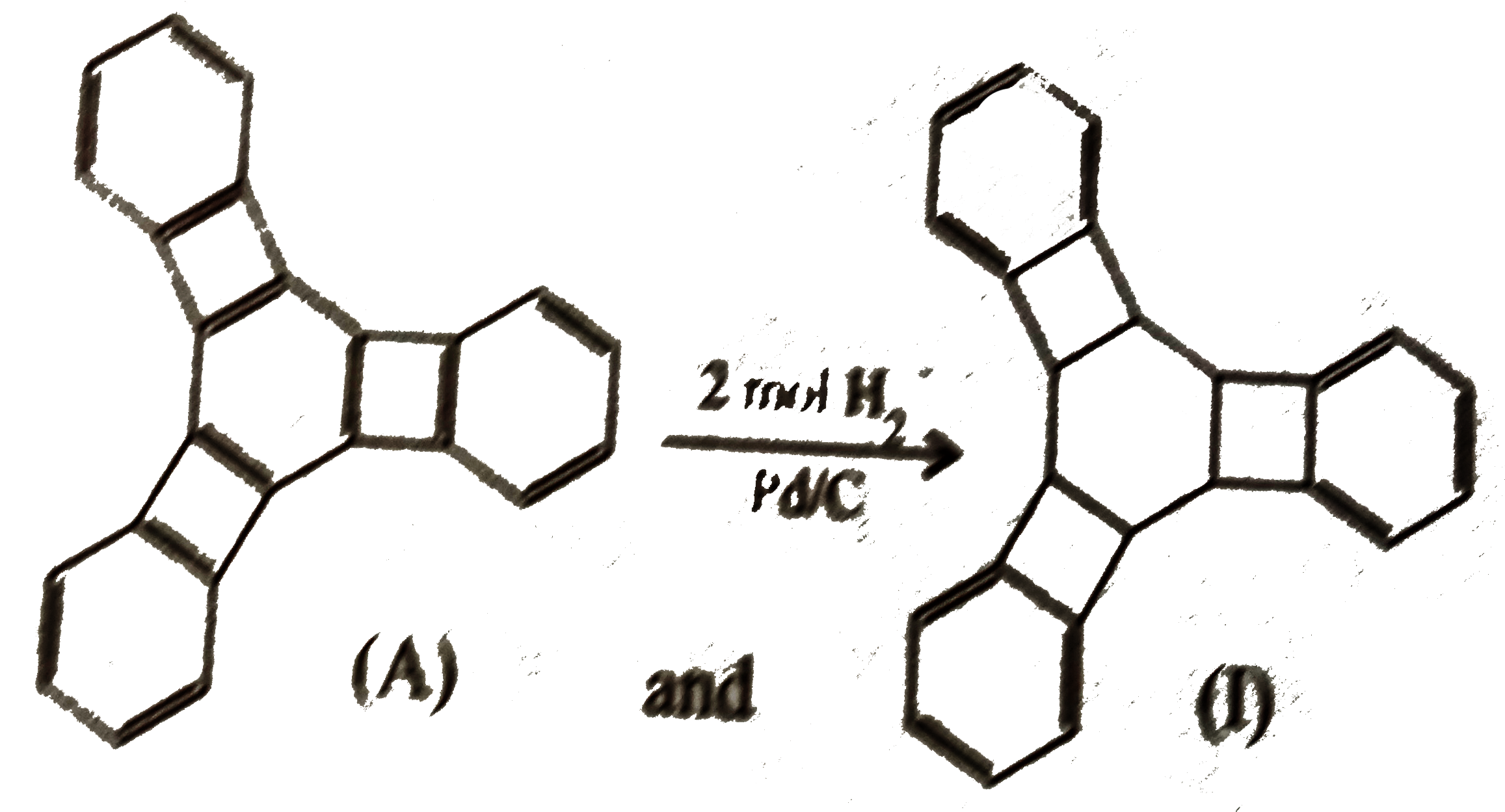 and
and 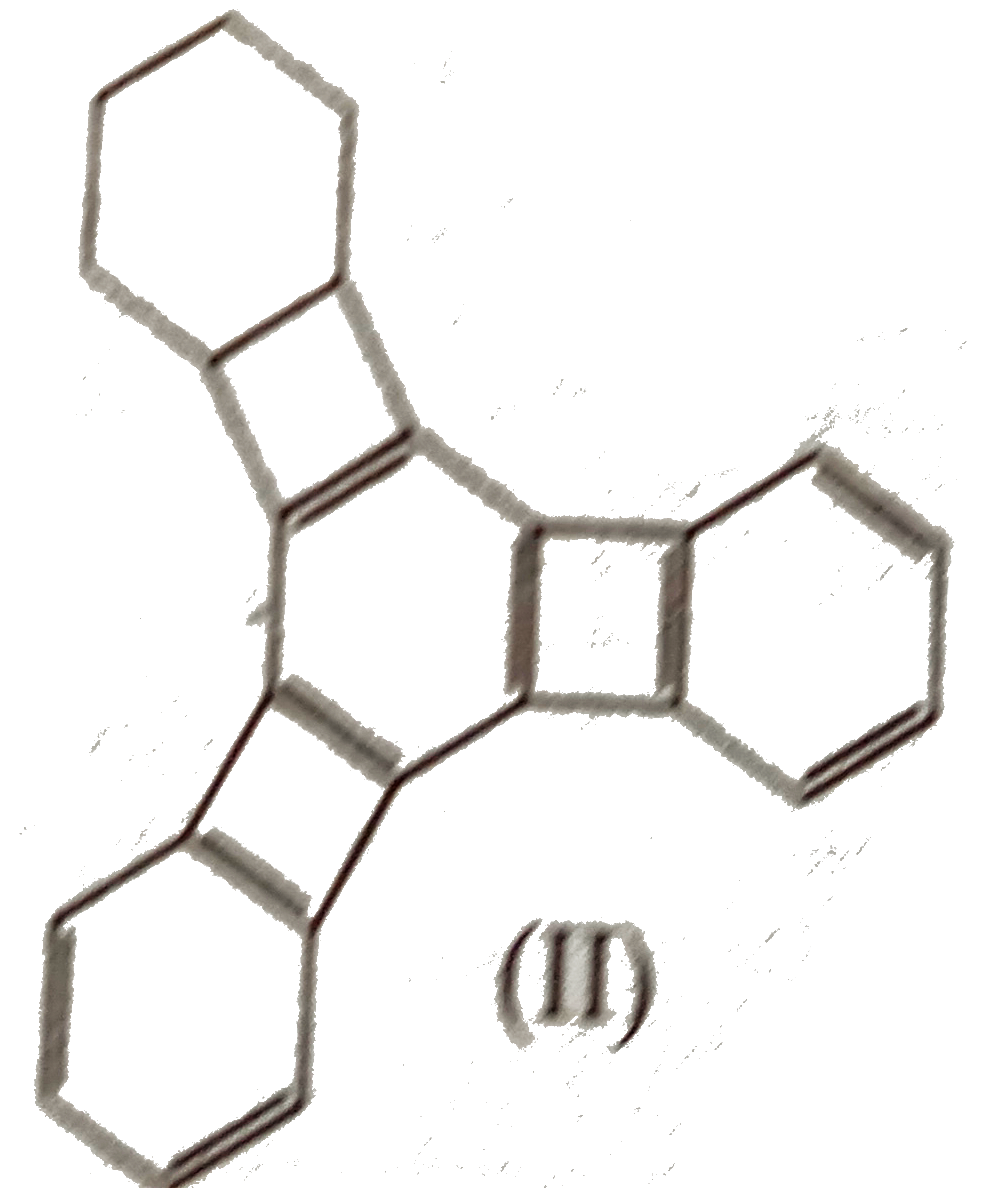
Statement- 2:
Due to the reduction of central ring, 3 four-membered anti-aromatic rings become stable to from (I). In (II), due to the reduction of terminal ring, only one anti-aromatic ring can be stabilised.
The correct Answer is:a
Step by step video, text & image solution for a. Statement- 1 and Statement- 2 are true, and state-ment- 2 is the correct explanation of Statement- 1. b. Statement- 1 and Statement- 2 are true but Statement- 2 is not the correct explanation of Statement- 1. c. Statement- 1 is true and Statement- 2 is false. d. Statement- 1 is false and Statement- 2 is true. e. Statement- 1 is false and Statement- 2 is false. Statement- 1: Compound (I) is formed not (II). and Statement- 2: Due to the reduction of central ring, 3 four-membered anti-aromatic rings become stable to from (I). In (II), due to the reduction of terminal ring, only one anti-aromatic ring can be stabilised. by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - CENGAGE CHEMISTRYCHAPTER - ALKANES AND CYCLOALKANESEXERCISE - MCQ20videos
ALKANES AND CYCLOALKANES
- BOOK - CENGAGE CHEMISTRYCHAPTER - ALKANES AND CYCLOALKANESEXERCISE - Single Correct45videos
ALKANES AND CYCLOALKANES
- BOOK - CENGAGE CHEMISTRYCHAPTER - ALKANES AND CYCLOALKANESEXERCISE - Fill in the Blanks1videos
ALKANES AND CYCLOALKANES
- BOOK - CENGAGE CHEMISTRYCHAPTER - ALKENES AND ALKADIENESEXERCISE - Single correct Answer14videos
ALKENES AND ALKADIENES
Similar Questions
Statement 1 is True: Statement 2 is True; Statement 2 is a correct explanation for statement 1 Statement 1 is true, Statement 2 is true;2 Statement 2 not a correct explanation for statement 1. Statement 1 is true, statement 2 is false Statement 1 is false, statement 2 is true Statement I: If A is obtuse angle I ABC, then tanB tanC<1 because Statement II: In ABC, tanA=tanB+tanCtanBtanC−1 a.A b. B c. C d. D
View SolutionStatement 1. If sin−1x=cos−1x,thenx=1√2, Statement 2. sin−1x+cos−1x=π2,1≤x←1 (A) Both Statement 1 and Statement 2 are true and Statement 2 is the correct explanation of Statement 1 (B) Both Statement 1 and Statement 2 are true and Statement 2 is not the correct explanatioin of Statement 1 (C) Statement 1 is true but Statement 2 is false. (D) Statement 1 is false but Statement 2 is true
View SolutionStatement 1 is True: Statement 2 is True; Statement 2 is a correct explanation for statement 1 Statement 1 is true, Statement 2 is true;2 Statement 2 not a correct explanation for statement 1. Statement 1 is true, statement 2 is false Statement 1 is false, statement 2 is true Statement I: If (log)((log)5x)5=2, thn x=5√5 Statement II: (log)xa=b, if a>0, then x=a1/b a.A b. B c. C d. D
View SolutionStatement 1. In a triangle ABC, if a:b:c=4:5:6,thenR:r=16:7,
Statement 2. In a triangle ABC, R:r=abc:4s
(A) Both Statement 1 and Statement 2 are true and Statement 2 is the correct explanation of Statement 1
(B) Both Statement 1 and Statement 2 are true and Statement 2 is not the correct explanatioin of Statement 1
(C) Statement 1 is true but Statement 2 is false.
(D) Statement 1 is false but Stastement 2 is trueView SolutionStatement 1 is True: Statement 2 is True; Statement 2 is a correct explanation for statement 1 Statement 1 is true, Statement 2 is true;2 Statement 2 not a correct explanation for statement 1. Statement 1 is true, statement 2 is false Statement 1 is false, statement 2 is true Statement I: sec2θ=4xy(x+y)2 is positive for all real values of x and y oly when x=y because Statement II: t2≥0∀t∈R a.A b. B c. C d. D
View SolutionStatement 1. If x,0,tan−1x+tan−1(1x)=π2, Statement 2. tan−1x+cot−1x=π2,∀xεR (A) Both Statement 1 and Statement 2 are true and Statement 2 is the correct explanation of Statement 1 (B) Both Statement 1 and Statement 2 are true and Statement 2 is not the correct explanatioin of Statement 1 (C) Statement 1 is true but Statement 2 is false. (D) Statement 1 is false but Statement 2 is true
View SolutionStatement 1. 2sinx+2cosx≥21−1√2 for all real x, Statement 2. For positive numbers, AM≥G.M. (A) Both Statement 1 and Statement 2 are true and Statement 2 is the correct explanation of Statement 1 (B) Both Statement 1 and Statement 2 are true and Statement 2 is not the correct explanation of Statement 1 (C) Statement 1 is true but Statement 2 is false. (D) Statement 1 is false but Statement 2 is true
View SolutionStatement 1. cosec−1(12+1√2)>sec−1(12+1√2), Statement 2. cosec^-1xgtsec^-1xif 1lexlesqrt(2) (A) Both Statement 1 and Statement 2 are true and Statement 2 is the correct explanation of Statement 1 (B) Both Statement 1 and Statement 2 are true and Statement 2 is not the correct explanatioin of Statement 1 (C) Statement 1 is true but Statement 2 is false. (D) Statement 1 is false but Statement 2 is true
View SolutionLet A be a 2×2 matrix Statement 1 : adj(adjA)=A Statement 2 : |adjA|=|A| (1) Statement1 is true, Statement2 is true, Statement2 is a correct explanation for statement1 (2) Statement1 is true, Statement2 is true; Statement2 is not a correct explanation for statement1. (3) Statement1 is true, statement2 is false. (4) Statement1 is false, Statement2 is true
View SolutionStatement I is True: Statement II is True; Statement II is a correct explanation for statement I Statement I is true, Statement II is true; Statement II not a correct explanation for statement I. Statement I is true, statement II is false Statement I is false, statement II is true Statement I: coses−1(cosec95)=π−95. because Statement II: cosec−1(cosecx)=π−x: ∀x∈[π2,3π2]−{π} a.A b. B c. C d. D
View Solution

