The resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitude is equal to half of the magnitude of the vector →B. Find out the angles between →A and →B.
 .
.
120∘
150∘
135∘
none of these
The correct Answer is:B
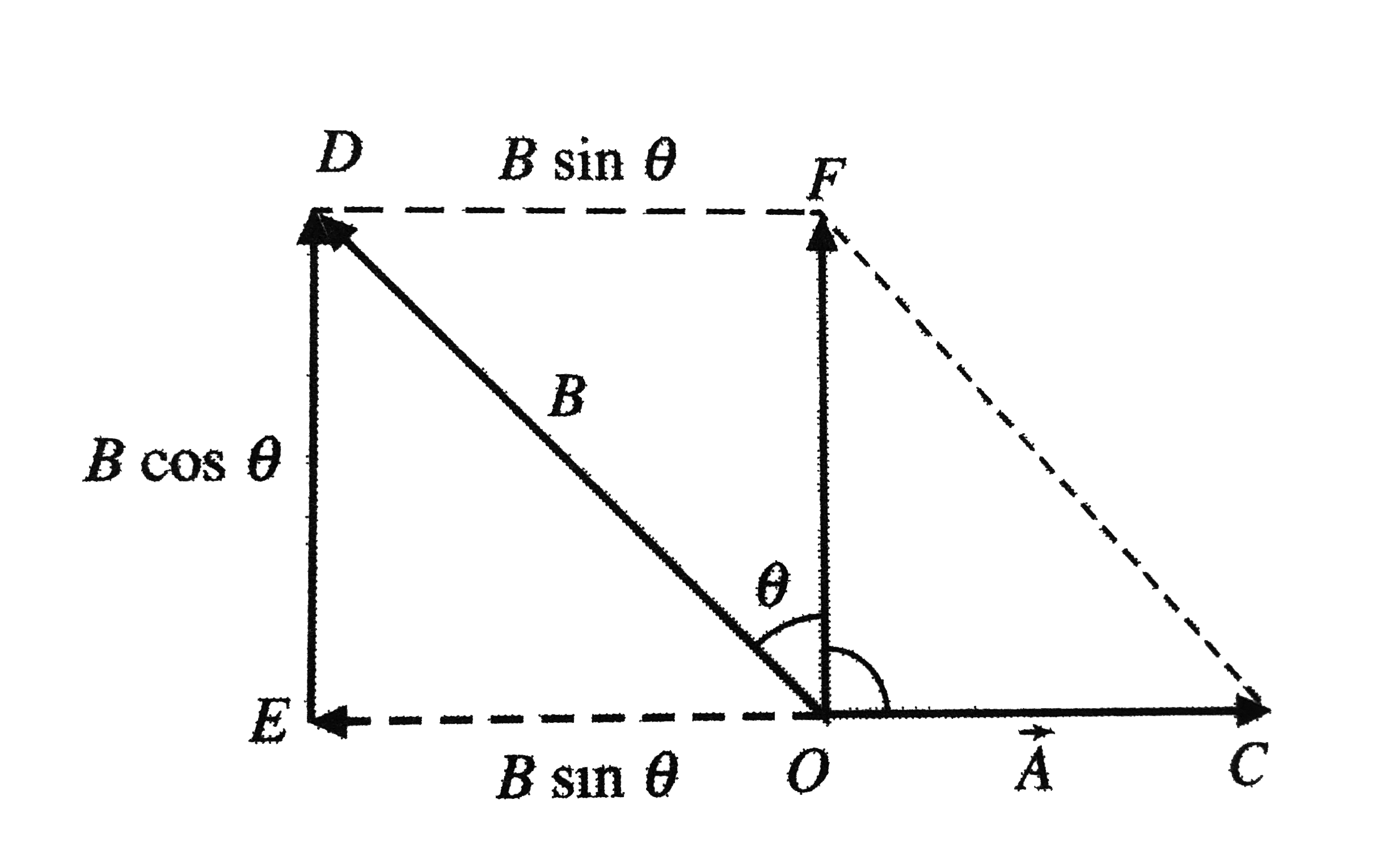
B2=√A2+B2+2ABcosθ
tan90∘=BsinθA+Bcosθ⇒A+Bcosθ=0
cosθ=−AB
Hence, from (i) B24=A2+B2−2A2⇒A=√3B2
⇒cosθ=−AB=−√32∵θ=150∘
Similar Questions
The resultant of two vectors →A and →b is perpendicular to the vector →A and its magnitude is equal to half the magnitude of vector →B. The angle between →A and →B is
View SolutionThe resultant of two vectors →A and →B is perpendicular to →A and equal to half of the magnitud of →B. Find angle between →B and →B?
View Solution
Knowledge Check
- Question 1 - Select One
The resultant of the vectors A and B is perpendicular to the vector A and its magnitude is equal to half the magnitude of vector B. The angle between →A and →B is :-
A120∘B150∘C135∘DNone of these - Question 2 - Select One
If for two vector →A and →B, sum (→A+→B) is perpendicular to the difference (→A−→B). The ratio of their magnitude is
A1B2C3DNone of these - Question 3 - Select One
If for two vector →A and →B, sum (→A+→B) is perpendicular to the difference (→A−→B). The ratio of their magnitude is
A1B2C3Dnone of these
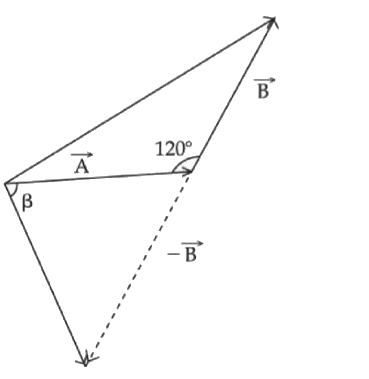
The angle between vector (→A) and (→A−→B) is :
 View Solution
View SolutionIf two vectors →Aand →Bmake angle 30∘and45∘ with their resultant and →B has magnitude equal to 10, then find magnitude of →A.
View SolutionThe vectors →A has a magnitude of 5 unit →B has a magnitude of 6 unit and the cross product of →Aand→B has a magnitude of 15 unit. Find the angle between →Aand→B.
View SolutionTwo vectors →A and →B have equal magnitudes. If magnitude of →A+→B is equal to n times the magnitude of →A−→B, then the angle between →A and →B is :-
View SolutionThe resultant of two vectors →Aand→B is →C. If the megnitude of →B is doubled, the new resultant vector becomes perpendicular to →A, then the magnitude of →C is
View Solution

