In the figure shown , A and B are free of to move. All the surfaces are smooth. $(0 < θ < 90^{\circ})$

A

the accelration of A will be more than $g sin θ$

B

the acceleration of A will beless than $g sin θ$

C

normal force on A due to B will be more than $m g cos θ$

D

normal force on A due to B will be less than $m g cos θ$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, D

$m a_{0} sin θ + N = m g cos θ$
$\Rightarrow m g cos θ$
$\Rightarrow N = m g cos θ - m a_{0} sin θ$
$\Rightarrow N < m g cos θ$
Hence, (D) is true.
$m a_{0} cos θ + m g sin θ = m a$
$\Rightarrow a = g sin θ + a_{0} cos θ$
Hence, acceleration of A
$= \sqrt{{(a - a_{0} cos θ)}_{0}^{2} + {(a_{0} sin θ)}_{0}^{2}} > g sin θ$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
In the figure shown $A$ and $B$ are free to move . All the surface are smooth. Mass of $A i s m$ . Then

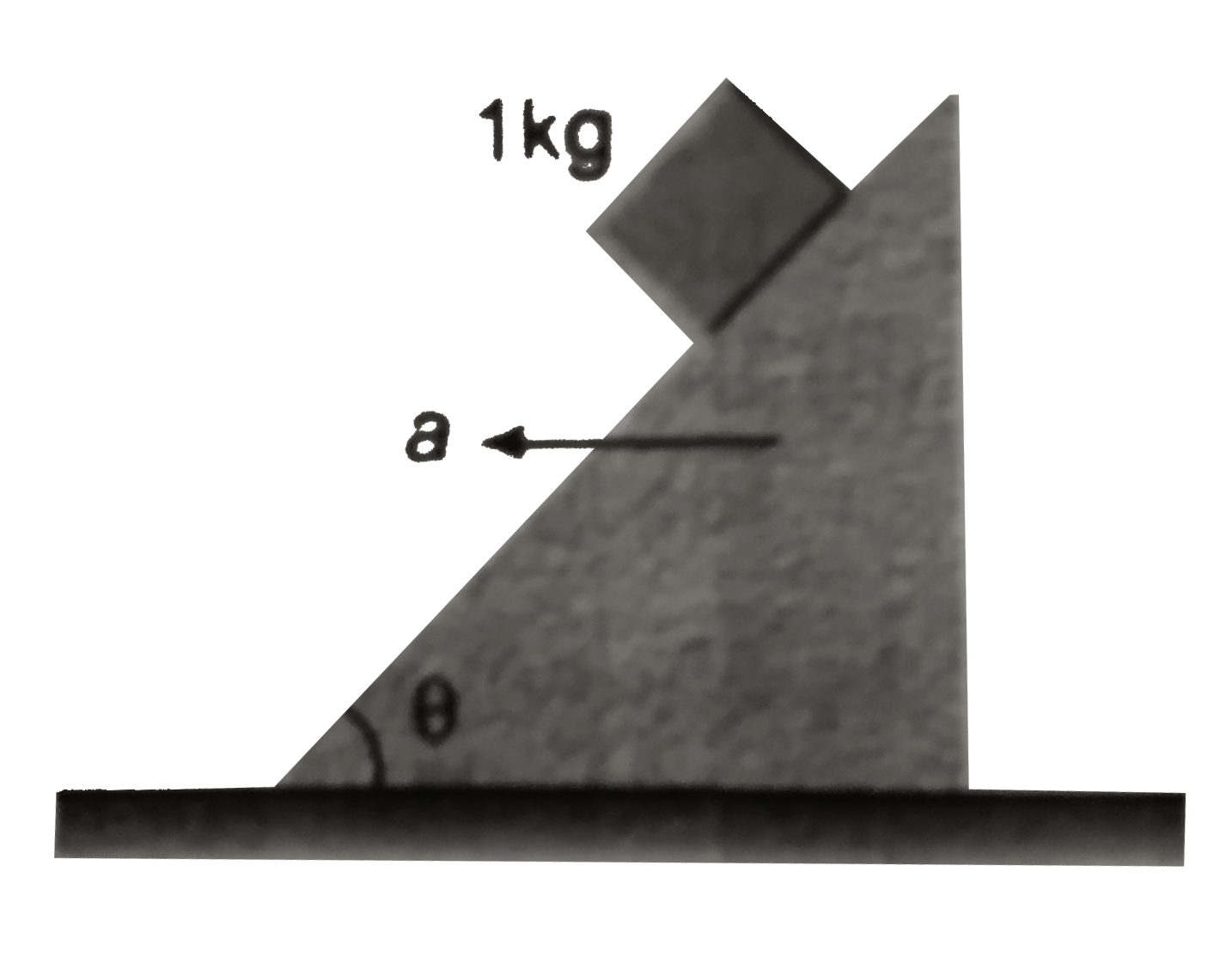Athe acceleration of $A$ will be more than $g sin θ$
Bthe acceleration of $A$ will be less than $g sin θ$
Cnormal reation $A$ due to $B$ will be more than $m g cos θ$
Dnormal reation $A$ due to $B$ will be less than $m g cos θ$
Question 2 - Select One
Which of the following relations is correct for $0 < θ < 90^{\circ}$ ?
A $sin θ = {sin}^{2} θ$
B $sin θ < {sin}^{2} θ$
C $sin θ > {sin}^{2} θ$
D $sin θ = s o {sec}^{2} θ$
Question 3 - Select One
The reflecting surface of two intersecting flat mirrors are at an angle $θ (0^{\circ} < θ < 90^{\circ})$ . As shown in Figure. For a light ray that strikes the horizontal mirror, the emerging ray intersects the incident ray at an angle $β$ . If one of the mirrors is rotated at $\frac{d θ}{d t} = 1^{\circ} / s$ , then the angle $β$ changes aat the rate of

A $1^{\circ} / s$
B $2^{\circ} / s$
C $- 1^{\circ} / s$
D $- 2^{\circ} / s$

CENGAGE PHYSICS-CENGAGE PHYSICS DPP-Multiple Correct Answer Type

Home
Ask Doubt
Profile