In Figure -6 , in an equilateral triangle ABC, AD is perpendicular to BC , BE is perpendicular to AC and CF is perpendicular to AB . Prove that 4(AD2+BE2+CF2)=9AB2
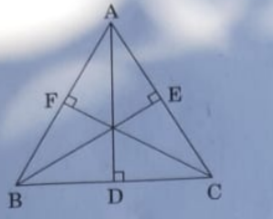
Step by step video & image solution for In Figure -6 , in an equilateral triangle ABC, AD is perpendicular to BC , BE is perpendicular to AC and CF is perpendicular to AB . Prove that 4 (AD^2 +BE^2 +CF^2)=9AB^2 by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CBSE BOARDS 2020BOOK - X BOARDSCHAPTER - CBSE BOARDS 2020EXERCISE - SECTION -A
22 Videos
- CBSE BOARDS 2020BOOK - X BOARDSCHAPTER - CBSE BOARDS 2020EXERCISE - QUESTION
42 Videos
- CBSE BOARDS 2020BOOK - X BOARDSCHAPTER - CBSE BOARDS 2020EXERCISE - SECTION C
34 Videos
- QUESTION PAPER 2022 TERM 1 SET 1 BASICBOOK - X BOARDSCHAPTER - QUESTION PAPER 2022 TERM 1 SET 1 BASICEXERCISE - SECTION-C (CASE STUDY)
10 Videos
Similar Questions
Knowledge Check
In triangle ABC, AD is prependicular to BC and DE is perpendicular to AB
 AabcdprqqBabcdqrpsCabcdspqrDabcdrpsq
AabcdprqqBabcdqrpsCabcdspqrDabcdrpsqLet ABC be an equilateral triangle. Let BE⊥CA meeting CA at E, then (AB2+BC2+CA2) is equal to :
A2AD2B3AD2C4AD2D5AD2If D id the mid-point of the side BC of a triangle ABC and AD is perpendicular to AC , then
Aa2+b2+c2=4b2Ba2+b2−c2=4b2Ca2−b2+c2=4b2Da2−b2−c2=4b2
In the figure, AD is perpendicular to BC, prove that AB+AC>2AD.

View SolutionABC is an equilateral triangle, and AD and BE are perpendiculars to BC and AC respectively. Prove that: 1. AD=BE 2. BD=CE [ΔABD=ΔBCE.]
View SolutionIn triangle ABC , ∠BAC=90∘ and AB=AC. Seg AP is perpendicular to side BC. D is any point on side BC. Prove that 2(AD)2=(BD)2+(CD)2
View SolutionIn △ ABC, AD is a median. Prove that AB + AC > 2AD
View SolutionIn a right triangle ABC, right angled at A, AD is drawn perpendicular to BC. Prove that:
AB2−BD2=AC2−CD2
View Solution
