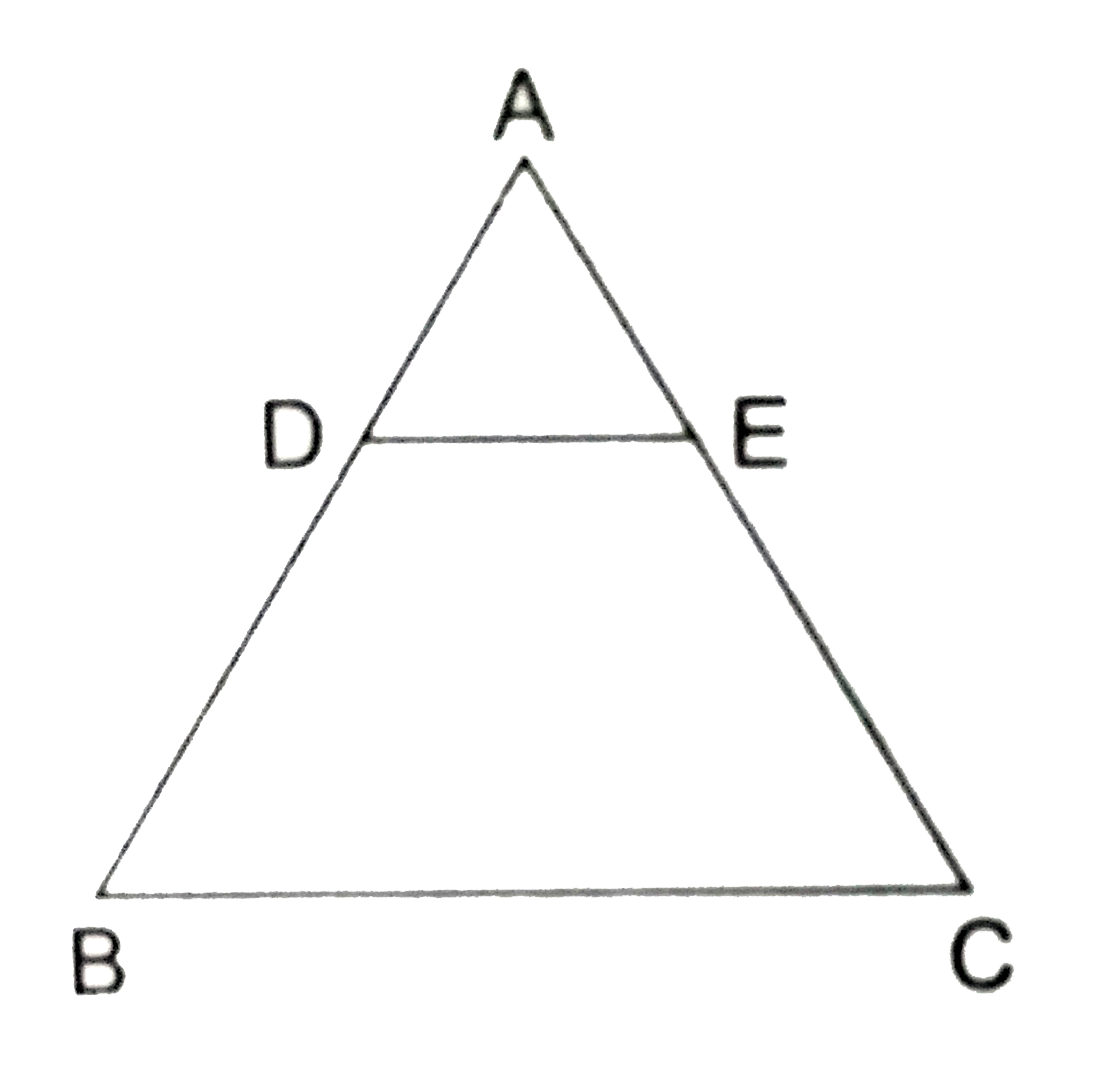
In triangle ABC, DE∣∣BCandADDB=3(5) . If AC = 4.8 cm .Find AE.
The correct Answer is:1.8cm
To solve the problem, we can use the properties of similar triangles. Since DE is parallel to BC, triangles ADE and ABC are similar. This means that the ratios of corresponding sides are equal.
Given:
- ADDB=35
- AC=4.8cm
Let:
- AD=3x
- DB=5x
Now, we can find AB:
AB=AD+DB=3x+5x=8x
Since triangles ADE and ABC are similar, we can set up the following ratio:
AEAC=ADAB
Substituting the values we have:
AE4.8=3x8x
The x cancels out:
AE4.8=38
Now, we can solve for AE:
AE=4.8⋅38
Calculating AE:
AE=4.8⋅0.375=1.8cm
Thus, the length of AE is 1.8cm.
- ADDB=35
- AC=4.8cm
- AD=3x
- DB=5x
AB=AD+DB=3x+5x=8x
AEAC=ADAB
AE4.8=3x8x
AE4.8=38
AE=4.8⋅38
AE=4.8⋅0.375=1.8cm
Topper's Solved these Questions
- DIKSHA QUESTIONS Book:OSWAL PUBLICATIONChapter:DIKSHA QUESTIONS Exercise:Unit -III: Coordinate Geometry (Coordinate Geometry ) (Long Answer Type Questions )
Explore 11 Videos
- DIKSHA QUESTIONS Book:OSWAL PUBLICATIONChapter:DIKSHA QUESTIONS Exercise:Unit -IV: Geometry (Triangles) (Multiple Choice Questions)
Explore 8 Videos
- DIKSHA QUESTIONS Book:OSWAL PUBLICATIONChapter:DIKSHA QUESTIONS Exercise:Unit -III: Coordinate Geometry (Coordinate Geometry ) (Multiple Choice Questions)
Explore 5 Videos
- COORDINATE GEOMETRYBook:OSWAL PUBLICATIONChapter:COORDINATE GEOMETRYExercise:SELF ASSESSMENT
Explore 20 Videos
- INTRODUCTION TO TRIGONOMETRY Book:OSWAL PUBLICATIONChapter:INTRODUCTION TO TRIGONOMETRY Exercise:Self - Assessment
Explore 15 Videos
Similar Questions
Knowledge Check
In ΔABC,DE∣∣BCsuch that ADBD=35. If AC=5.6cm, then AE is equal to
A4.2 cm.B3.1 cm.C2.8 cm.D2.1 cm.
In ΔABC,DE∣∣BC such that ADDB=35 . If AC=5.6cm then, AE=?
View SolutionIn the figure DE is parallel to BC and ADDB=23 if AE = 3.7 cm find EC.
View SolutionIn the given figure, DE||BC and ADDB=23if AE=3.7 cm , find EC.

View SolutionIn △ABC,D and E are points an the sides AB and AC repectivaly such that DEllBC . If ADDB=34 and AC=15 cm . Find AE.
View SolutionIn a ΔABC, if DE is parallel to BC, ADDB=34 and AC = 15 cm, then find the length AE.
View SolutionIf DE||BC in △ABC where D and E are points on AB and AC respectively. If ADDB=815 and EC = 3.5 cm , find AE.
View SolutionIn ΔABC, when DE || BC and AD = x, DB = 3x + 4, AE = x + 3 and EC = 3x + 19 then value of x is:
View Solution