If ABC and DEF are similar such that 2 AB=DE and BC=8cm , then EF= (a) 16cm (b) 12cm (c) 8cm (d) 4cm.
16cm
12cm
8cm
4cm
Step by step video & image solution for If A B C and D E F are similar such that 2\ A B=D E and B C=8c m , then E F= (a) 16cm (b) 12cm (c) 8cm (d) 4cm. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILARITYBOOK - UNIQUE PUBLICATIONCHAPTER - SIMILARITYEXERCISE - Unique practise Session (4 Marks Question)
2 Videos
- QUADRATIC EQUATIONS BOOK - UNIQUE PUBLICATIONCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNMENT
6 Videos
- STATISTICS BOOK - UNIQUE PUBLICATIONCHAPTER - STATISTICS EXERCISE - PROBLEM SET
6 Videos
Similar Questions
If ABC and DEF are similar such that 2 AB=DE and BC=8cm , then EF= (a) 16cm (b) 12cm (c) 8cm (d) 4cm.
View SolutionABCPQR such that ar(ABC)=4ar(PQR). If BC=12cm , then QR= (a) 9cm (b) 10cm (c) 6cm (d) 8cm
View SolutionP is the mid-point of side BC of a parallelogram ABCD such that ∠BAP=∠DAP. If AD=10cm, then CD= 5cm (b) 6cm (c) 8cm (d) 10cm
View SolutionIf ABCDEF such that DE=3cm , EF=2cm , DF=2.5cm , BC=4cm , then perimeter of ABC is (a) 18cm (b) 20cm (c) 12cm (d) 15cm
View SolutionIn Figure, ABCD is a parallelogram. If AB=12cm,AE=7.5cm,CF=15cm, then AD=
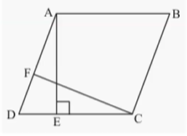
(a) 3 cm
(b) 6 cm
(c) 8 cm
(d) 10.5 cm
View SolutionIn ABC and DEF , it is being given that: AB=5cm, BC=4cm and CA=4.2cm ; DE=10cm , EF=8cm and FD=8.4cm . If AL⊥BC and DM⊥EF , find AL:DM .
View SolutionIf ABC and DEF are two triangles such that ABDE=BCEF=CAFD=25 , then Area(ABC):Area(DEF)= 2:5 (b) 4:25 (c) 4:15 (d) 8:125
View SolutionABCDEF , ar(ABC)=9cm2 , ar(DEF)=16cm2 . If BC=2.1cm , then the measure of EF is 2.8cm (b) 4.2cm (c) 2.5cm (d) 4.1cm
View SolutionABCD is a parallelogram and EandF are the centroids of triangles ABD and BCD respectively, then EF= (a)AE (b) BE (c) CE (d)DE
View SolutionIf the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2 , then its radius is (a) 12 cm (b) 16 cm (c) 8 cm (d) 10 cm
View Solution
