In the given fig O is centre of circle, $∠ A C O = 35^{\circ}$ and $∠ A B O = 45^{\circ}$ , then what is the value of $∠ B O C$

Video Solution

Text Solution

Verified by Experts

from the given figure we can conclude that
$∠ B A C = 45^{\circ} + 35^{\circ}$
$= 80^{\circ}$
Now as we can see that
$∠ B O C = 2 ∠ B A C$
$∠ B O C = 2 \times 80^{\circ}$
$= 160^{\circ}$
Answer

Updated on:21/07/2023

|

Class 9 MATHS CIRCLES

Similar Questions

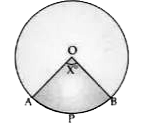
In given fig, O is the centre of a circle. If the area of the sector OAPB is $\frac{5}{36}$ times the area of the cicle, then find the value of x.

View Solution
In the given figure O is the center of the circle and /_BOC = 120^@ If so /_BPC What will be the value of?
View Solution
In the given figure O is the centre of the circle. Tangents at A and B meet at C. If $∠ A C O = 30^{\circ}$ find

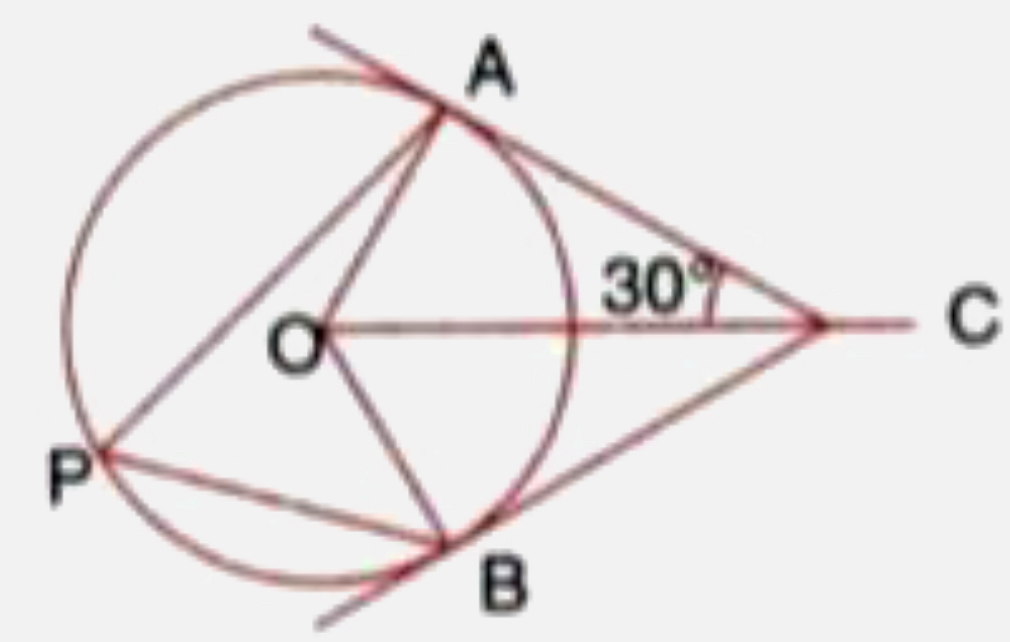
(i) $∠ B C O$
(ii) $∠ A O B$
(iii) $∠ A P B$
View Solution
In the given figure, O is the centre of the circle. The value of x is

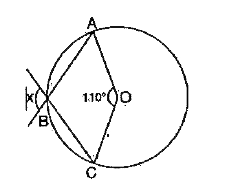
View Solution
In the given figures, value of y (O is the centre of the circle) is

View Solution
AB is a diameter of the circle with centre O, CD is chord of the circle. If $∠ B O C = 120^{\circ}$ , then the value of $∠ A D C$ is
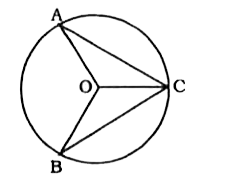
View Solution
In the given figure, O is the centre of the circle, $∠ C A O$ = $35^{\circ}$ and $∠ C B O$ = $45^{\circ}$ . What is the value (In degrees) of $∠ A O B$ ?

View Solution
The chord AB of a circle of centre O subtends an angle $θ$ with the tangent at A to the circle. Then measure of $∠ A B O$ is :
View Solution

Recommended Questions

Home
Ask Doubt
Profile