In the accompanying, diagram a fair spinner is placed at the centre O of the circle, Diameter AOB and radius OC divide the circle into three rigions lebelled X,YandZ . If ∠BOC=450. What is the probability that the spinner will land in the region X?
(##XRD13_E0126_s01##)
Given ∠BOC=45∘
∠AOC=180−∠5=135∘
Area of circle =πr2
Area of region x=θ360∘×πr2
=135360×πr2=38πr2
Probability that the spinner will land in the region
X=((area of the region x)/(area of the circle))
=38πr2πr2=38
Topper's Solved these Questions
Similar Questions
In the accompanying, diagram a fair spinner is placed at the centre O of the circle, Diameter AOB and radius OC divide the circle into three rigions lebelled X,YandZ . If ∠BOC=450. What is the probability that the spinner will land in the region X?
View SolutionIn the given figure, AB and PQ are perpendicular diameters of the circle whose centre is O and radius OA = 7 cm. Find the area of the shade region.

View Solution
Knowledge Check
In the given figure, AB and AC are tangents to the circle at B and C respectively and O is the centre of the circle, then x equals
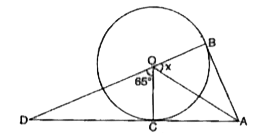 A65∘B32.5∘C57.5∘D45∘
A65∘B32.5∘C57.5∘D45∘
In the given diagram, 'O' is the centre of the circle and AC is the diameter. ∠ADB is 120∘. Radius of the circle is 6 cm, what is the area of the triangle ABC?
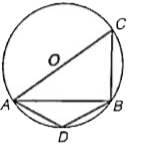
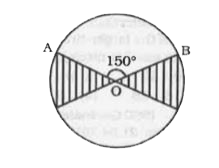
View SolutionO is the centre of the circle and ∠AOB=150∘, and the shaded portion is x part of the circular region, then x = ?
View SolutionIn Figure, O and O' are centres of two circles intersecting at B and C.ACD is a straight line, find x
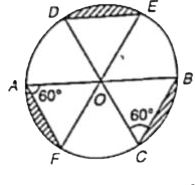
View SolutionIn the adjoining figure O is the centre of the circle with radius 'r' AB, CD and EF are the diameters of the circle. ∠OAF=∠OCB=60∘. What is the area of the shaded region?
View SolutionIn the circle with centre O and A,B,C are the points on the circle, ∠AOB=60∘. Find ∠ACB
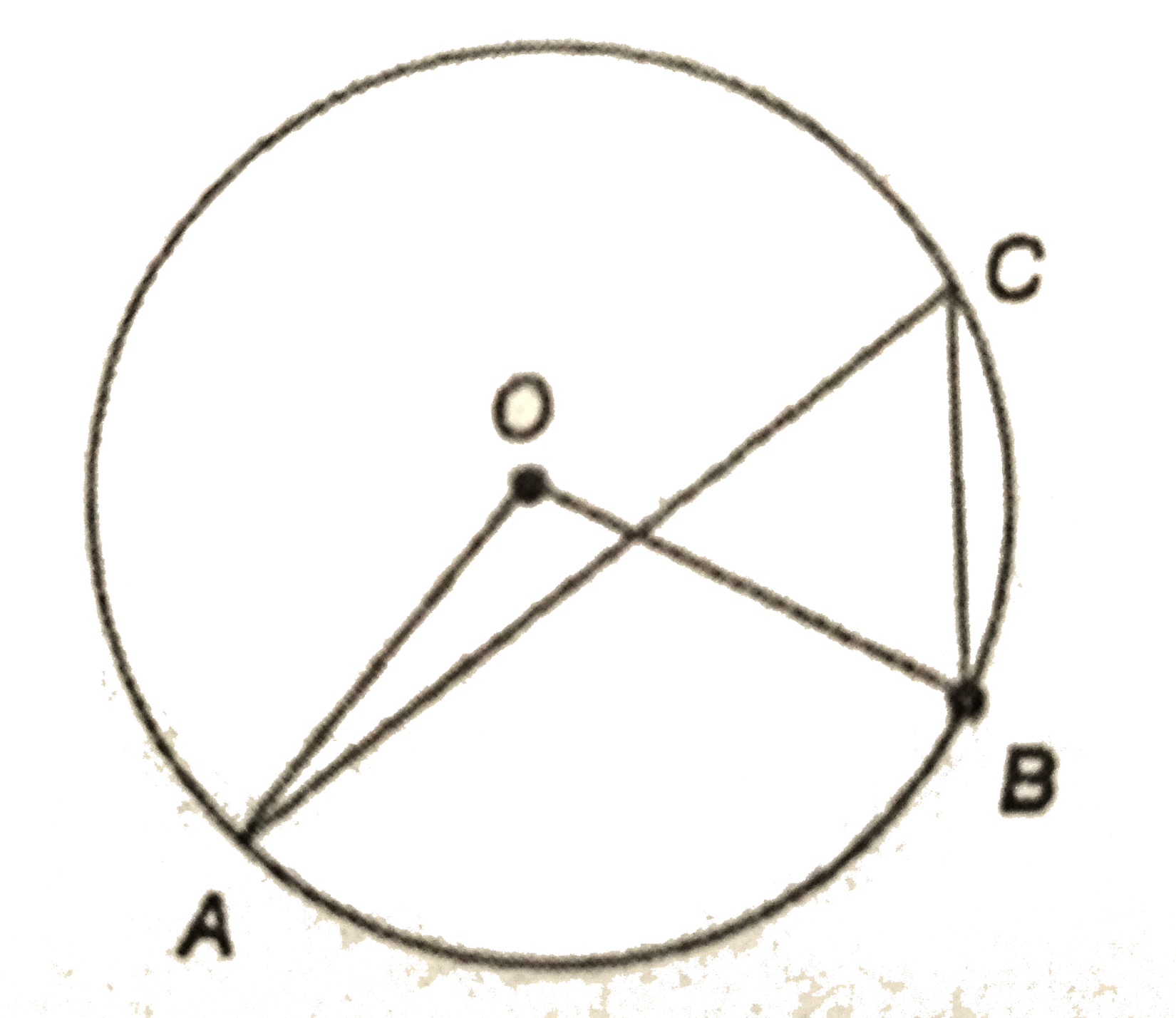
View SolutionABC is an equilateral triangle of side 6 cm, a circle, centre O, passes through the vertices A, B, and C. Find the radius of the circle.
View SolutionIn the figure, O is the centre of the circle. If ∠ADC=140∘, then what is the value of x?
View Solution
