The angle between vectors $(\to A \times \to B)$ and $(\to B \times \to A)$ is

A

$π / 2$

B

$π / 3$

C

$π$

D

$π / 4$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

We know that $\to A \times \to B = - (\to B \times \to A)$ because the angle between these two is always $90^{\circ}$
But if the angle between $\to A$ and $\to B$ is $0 or π$ . Then $\to A \times \to B = \to B \times \to A = 0$

|

Updated on:21/07/2023

Class 11 PHYSICS VECTOR

Topper's Solved these Questions

BOOK - A2ZCHAPTER - VECTORSEXERCISE - Problems Based On Mixed Concepts
32videos
VECTORS
BOOK - A2ZCHAPTER - VECTORSEXERCISE - Assertion Reasoning
17videos
VECTORS
BOOK - A2ZCHAPTER - VECTORSEXERCISE - Dot Product
22videos
VECTORS
BOOK - A2ZCHAPTER - UNIT, DIMENSION AND ERROR ANALYSISEXERCISE - Chapter Test
28videos
UNIT, DIMENSION AND ERROR ANALYSIS
BOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test
30videos
WAVES AND ACOUSTICS

Similar Questions

Knowledge Check

Question 1 - Select One
The cross product of two vectors gives a vector perpendicular to the plane containing the vectors.

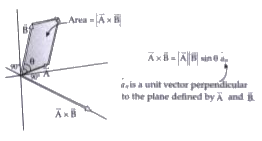
The angle between $\to a \times \to b$ and $\to b \times \to a$ is ___________.
A0
B $π$
C $\frac{π}{2}$
D $\frac{π}{4}$
Question 2 - Select One
The angle between $\to A + \to B$ and $\to A \times \to B$ is
A0
B $π / 4$
C $π / 2$
D $π$
Question 3 - Select One
$\to A$ and $\to B$ are two Vectors and $θ$ is the angle between them, if $∣ ∣ \to A \times \to B ∣ ∣ = \sqrt{3} (\to A . \to B)$ the value of $θ$ is
A $60^{\circ}$
B $45^{\circ}$
C $30^{\circ}$
D $90^{\circ}$

A2Z-VECTORS-Cross Product

Home
Ask Doubt
Profile